Published online by Cambridge University Press: 19 April 2016
The rheology of the steady uniform shear flow of smooth inelastic spheres is analysed by choosing the anisotropic/triaxial Gaussian as the single-particle distribution function. An exact solution of the balance equation for the second-moment tensor of velocity fluctuations, truncated at the ‘Burnett order’ (second order in the shear rate), is derived, leading to analytical expressions for the first and second (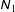 $\unicode[STIX]{x1D615}_{1}$ and
$\unicode[STIX]{x1D615}_{1}$ and  $\unicode[STIX]{x1D615}_{2}$) normal stress differences and other transport coefficients as functions of density (i.e. the volume fraction of particles), restitution coefficient and other control parameters. Moreover, the perturbation solution at fourth order in the shear rate is obtained which helped to assess the range of validity of Burnett-order constitutive relations. Theoretical expressions for both
$\unicode[STIX]{x1D615}_{2}$) normal stress differences and other transport coefficients as functions of density (i.e. the volume fraction of particles), restitution coefficient and other control parameters. Moreover, the perturbation solution at fourth order in the shear rate is obtained which helped to assess the range of validity of Burnett-order constitutive relations. Theoretical expressions for both 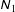 $\unicode[STIX]{x1D615}_{1}$ and
$\unicode[STIX]{x1D615}_{1}$ and 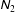 $\unicode[STIX]{x1D615}_{2}$ and those for pressure and shear viscosity agree well with particle simulation data for the uniform shear flow of inelastic hard spheres for a large range of volume fractions spanning from the dilute regime to close to the freezing-point density (
$\unicode[STIX]{x1D615}_{2}$ and those for pressure and shear viscosity agree well with particle simulation data for the uniform shear flow of inelastic hard spheres for a large range of volume fractions spanning from the dilute regime to close to the freezing-point density (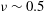 ${\it\nu}\sim 0.5$). While the first normal stress difference
${\it\nu}\sim 0.5$). While the first normal stress difference 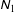 $\unicode[STIX]{x1D615}_{1}$ is found to be positive in the dilute limit and decreases monotonically to zero in the dense limit, the second normal stress difference
$\unicode[STIX]{x1D615}_{1}$ is found to be positive in the dilute limit and decreases monotonically to zero in the dense limit, the second normal stress difference  $\unicode[STIX]{x1D615}_{2}$ is negative and positive in the dilute and dense limits, respectively, and undergoes a sign change at a finite density due to the sign change of its kinetic component. It is shown that the origin of
$\unicode[STIX]{x1D615}_{2}$ is negative and positive in the dilute and dense limits, respectively, and undergoes a sign change at a finite density due to the sign change of its kinetic component. It is shown that the origin of 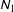 $\unicode[STIX]{x1D615}_{1}$ is tied to the non-coaxiality (
$\unicode[STIX]{x1D615}_{1}$ is tied to the non-coaxiality (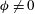 ${\it\phi}\neq 0$) between the eigendirections of the second-moment tensor
${\it\phi}\neq 0$) between the eigendirections of the second-moment tensor 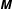 $\unicode[STIX]{x1D648}$ and those of the shear tensor
$\unicode[STIX]{x1D648}$ and those of the shear tensor 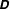 $\unicode[STIX]{x1D63F}$. In contrast, the origin of
$\unicode[STIX]{x1D63F}$. In contrast, the origin of 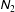 $\unicode[STIX]{x1D615}_{2}$ in the dilute limit is tied to the ‘excess’ temperature (
$\unicode[STIX]{x1D615}_{2}$ in the dilute limit is tied to the ‘excess’ temperature (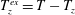 $T_{z}^{ex}=T-T_{z}$, where
$T_{z}^{ex}=T-T_{z}$, where 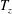 $T_{z}$ and
$T_{z}$ and 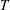 $T$ are the
$T$ are the  $z$-component and the average of the granular temperature, respectively) along the mean vorticity (
$z$-component and the average of the granular temperature, respectively) along the mean vorticity ( $z$) direction, whereas its origin in the dense limit is tied to the imposed shear field.
$z$) direction, whereas its origin in the dense limit is tied to the imposed shear field.