Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Blanco-Trejo, S.
Herrada, M. A.
Gañán-Calvo, A. M.
and
Montanero, José M.
2019.
Electrospray cone-jet mode for weakly viscoelastic liquids.
Physical Review E,
Vol. 100,
Issue. 4,
Cisquella-Serra, Albert
Magnani, Marco
Gual-Mosegui, Álvaro
Holmberg, Sunshine
Madou, Marc
and
Gamero-Castaño, Manuel
2019.
Study of the electrostatic jet initiation in near-field electrospinning.
Journal of Colloid and Interface Science,
Vol. 543,
Issue. ,
p.
106.
Zhang, Shichao
Liu, Hui
Tang, Ning
Ge, Jianlong
Yu, Jianyong
and
Ding, Bin
2019.
Direct electronetting of high-performance membranes based on self-assembled 2D nanoarchitectured networks.
Nature Communications,
Vol. 10,
Issue. 1,
Coffman, Chase S.
Martínez-Sánchez, Manuel
and
Lozano, Paulo C.
2019.
Electrohydrodynamics of an ionic liquid meniscus during evaporation of ions in a regime of high electric field.
Physical Review E,
Vol. 99,
Issue. 6,
Gamero-Castaño, Manuel
and
Magnani, M.
2019.
The minimum flow rate of electrosprays in the cone-jet mode.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
553.
Gamero-Castaño, M.
2019.
Dissipation in cone-jet electrosprays and departure from isothermal operation.
Physical Review E,
Vol. 99,
Issue. 6,
Magnani, Marco
and
Gamero, Manuel
2019.
Modeling of the Dissipation and Self-Heating of the Propellant in Electrospray Thrusters.
López-Herrera, Jose M.
Herrada, Miguel A.
Gamero-Castaño, Manuel
and
Gañán-Calvo, Alfonso M.
2020.
A numerical simulation of coaxial electrosprays.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Montanero, J M
and
Gañán-Calvo, A M
2020.
Dripping, jetting and tip streaming.
Reports on Progress in Physics,
Vol. 83,
Issue. 9,
p.
097001.
Davis, Eric J.
Walker, David
Gibney, Molly
and
Clowers, Brian H.
2021.
Optical and mass spectral characterization of the electrospray ionization/corona discharge ionization interface.
Talanta,
Vol. 224,
Issue. ,
p.
121870.
Zhang, Jinrui
Cai, Guobiao
Liu, Xuhui
He, Bijiao
and
Wang, Weizong
2021.
Molecular dynamics simulation of ionic liquid electrospray: Revealing the effects of interaction potential models.
Acta Astronautica,
Vol. 179,
Issue. ,
p.
581.
Gamero-Castaño, Manuel
and
Cisquella-Serra, Albert
2021.
Electrosprays of highly conducting liquids: A study of droplet and ion emission based on retarding potential and time-of-flight spectrometry.
Physical Review Fluids,
Vol. 6,
Issue. 1,
Xia, Huihui
Yu, Boyang
Chang, Kai
Zhao, Xinyan
and
Deng, Weiwei
2021.
Shaping electrospray deposition profile by a quadrupole: From circular to elliptical patterns.
Journal of Aerosol Science,
Vol. 154,
Issue. ,
p.
105739.
Narváez-Muñoz, Christian
Ryzhakov, Pavel
and
Pons-Prats, Jordi
2021.
Determination of the Operational Parameters for the Manufacturing of Spherical PVP Particles via Electrospray.
Polymers,
Vol. 13,
Issue. 4,
p.
529.
Guan, Yin
Wu, Shuang
Wang, Mengduo
Tian, Yu
Lai, Wuxing
and
Huang, YongAn
2022.
Numerical analysis of electrohydrodynamic jet printing under constant and step change of electric voltages.
Physics of Fluids,
Vol. 34,
Issue. 6,
Guan, Yin
Wu, Shuang
Wang, Mengduo
Tian, Yu
Yu, Chuanpeng
Lai, Wuxing
and
Huang, YongAn
2022.
Numerical investigation of high-frequency pulsating electrohydrodynamic jet at low electric Bond numbers.
Physics of Fluids,
Vol. 34,
Issue. 1,
Misra, Kaartikey
and
Gamero-Castaño, Manuel
2022.
Leaky-dielectric phase field model for the axisymmetric breakup of an electrified jet.
Physical Review Fluids,
Vol. 7,
Issue. 6,
Perez-Lorenzo, Luis Javier
and
Fernandez de la Mora, Juan
2022.
Probing electrically driven nanojets by energy and mass analysis in vacuo.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Gallud, Ximo
and
Lozano, Paulo C.
2022.
The emission properties, structure and stability of ionic liquid menisci undergoing electrically assisted ion evaporation.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Petro, Elaine M.
Gallud, Ximo
Hampl, Sebastian K.
Schroeder, Madeleine
Geiger, Carl
and
Lozano, Paulo C.
2022.
Multiscale modeling of electrospray ion emission.
Journal of Applied Physics,
Vol. 131,
Issue. 19,
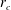 $r_{c}$, is largely invariant regardless of the physical properties and flow rates of the liquids. The surface charge falls below its equilibrium value along the transition from cone to jet, with a deficit that increases with the ratio between the electrical relaxation and flow residence times. Several characteristics of the cone jet are functions of the dielectric constant, which is consistent with the importance of charge relaxation effects (i.e. with the absence of surface charge equilibrium). The electric energy transferred to the transition region is largely transformed into viscous and ohmic dissipation, and conversion into kinetic energy only dominates once most of the current is fixed on the surface.
$r_{c}$, is largely invariant regardless of the physical properties and flow rates of the liquids. The surface charge falls below its equilibrium value along the transition from cone to jet, with a deficit that increases with the ratio between the electrical relaxation and flow residence times. Several characteristics of the cone jet are functions of the dielectric constant, which is consistent with the importance of charge relaxation effects (i.e. with the absence of surface charge equilibrium). The electric energy transferred to the transition region is largely transformed into viscous and ohmic dissipation, and conversion into kinetic energy only dominates once most of the current is fixed on the surface.