Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T19:58:37.706Z Has data issue: false hasContentIssue false
  • English
  • Français

On the convergence of the normal form transformation in discrete Rossby and drift wave turbulence

Published online by Cambridge University Press:  10 December 2019

Shane G. Walsh Open the ORCID record for Shane G. Walsh [Opens in a new window]  and
Miguel D. Bustamante Open the ORCID record for Miguel D. Bustamante [Opens in a new window]
Shane G. Walsh*
Affiliation:
School of Mathematics and Statistics, University College Dublin, Belfield, Dublin4, Ireland
Miguel D. Bustamante
Affiliation:
School of Mathematics and Statistics, University College Dublin, Belfield, Dublin4, Ireland
*
†Email address for correspondence: shanewalsh11235@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

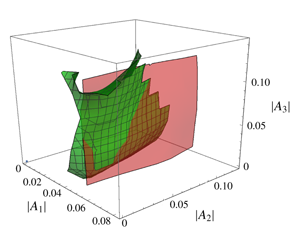
We study numerically the region of convergence of the normal form transformation for the case of the Charney–Hasagawa–Mima (CHM) equation to investigate whether certain finite amplitude effects can be described in normal form coordinates. Specifically, we consider a Galerkin truncation of the CHM equation to four Fourier modes, and ask: Can the finite amplitude phenomenon known as precession resonance (Bustamante et al., Phys. Rev. Lett., vol. 113, 2014, 084502) be described by the normal form variables of wave turbulence theory? The answer is no, due to the failure of convergence of the normal form transformation at the wave amplitudes required for precession resonance. We show this by first characterising precession resonance in the original system, then, searching for this resonance in the normal form equations of motion. We find a large discrepancy between the dynamics of the original system and the transformed normal form system. This prompts an investigation into the convergence of the transformation in the state space of wave amplitudes. We find that the numerically calculated region of convergence is a region of finite wave amplitudes, well beyond the usual limit of weak nonlinearity. However, the amplitudes at the boundary of this region of convergence (i.e. the amplitudes at which the normal form transformation begins to diverge) match closely with the amplitudes at which precession resonance occurs in the original system. We conclude that the precession resonance mechanism cannot be explained by the usual methods of normal forms in wave turbulence theory, so a more general theory for intermediate nonlinearity is required.

JFM classification

Turbulent Flows: Wave-turbulence interactions Nonlinear Dynamical Systems: Low-dimensional models
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A28
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berti, M., Feola, R. & Pusateri, F.2018 Birkhoff normal form and long time existence for periodic gravity water waves. arXiv:1810.11549.Google Scholar
Biferale, L. 2003 Shell models of energy cascade in turbulence. Annu. Rev. Fluid Mech. 35 (1), 441–468.CrossRefGoogle Scholar
Bruno, A. D., Hovingh, W. & Coleman, C. S. 2011 Local Methods in Nonlinear Differential Equations: Part I The Local Method of Nonlinear Analysis of Differential Equations Part II The Sets of Analyticity of a Normalizing Transformation. Springer.Google Scholar
Bustamante, M. D., Quinn, B. & Lucas, D. 2014 Robust energy transfer mechanism via precession resonance in nonlinear turbulent wave systems. Phys. Rev. Lett. 113, 084502.CrossRefGoogle ScholarPubMed
Craig, W. & Worfolk, P. A. 1995 An integrable normal form for water waves in infinite depth. Physica D 84 (3), 513–531.CrossRefGoogle Scholar
Craik, A. D. D. 1988 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Dyachenko, A. I., Lvov, Y. V. & Zakharov, V. E. 1995 Five-wave interaction on the surface of deep fluid. Physica D 87 (1), 233–261; Proceedings of the Conference on The Nonlinear Schrodinger Equation.CrossRefGoogle Scholar
Dyachenko, A. I. & Zakharov, V. E. 1994 Is free-surface hydrodynamics an integrable system? Phys. Lett. A 190 (2), 144–148.CrossRefGoogle Scholar
Gandhi, P., Knobloch, E. & Beaume, C. 2015 Dynamics of phase slips in systems with time-periodic modulation. Phys. Rev. E 92, 062914.Google ScholarPubMed
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.CrossRefGoogle Scholar
Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N. & Dudley, J. M. 2010 The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6, 790–795.CrossRefGoogle Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.CrossRefGoogle Scholar
Krasitskii, V. 1990 Canonical transformation in a theory of weakly nonlinear waves with a nondecay dispersion law. Sov. Phys. JETP 71, 921–927.Google Scholar
Krikorian, R.2019 On the divergence of Birkhoff Normal Forms. arXiv:1906.01096.Google Scholar
Lucas, D. & Kerswell, R. 2017 Sustaining processes from recurrent flows in body-forced turbulence. J. Fluid Mech. 817, R3.CrossRefGoogle Scholar
Lucas, D. & Kerswell, R. R. 2015 Recurrent flow analysis in spatiotemporally chaotic 2-dimensional Kolmogorov flow. Phys. Fluids 27 (4), 045106.CrossRefGoogle Scholar
Lynch, P. 2009 On resonant Rossby–Haurwitz triads. Tellus A 61 (3), 438–445.CrossRefGoogle Scholar
Mailybaev, A. A. 2013 Blowup as a driving mechanism of turbulence in shell models. Phys. Rev. E 87, 053011.Google ScholarPubMed
Nazarenko, S. 2011 Wave Turbulence. Springer.CrossRefGoogle Scholar
Perez-Marco, R. 2003 Convergence or generic divergence of the Birkhoff normal form. Ann. Maths 157 (2), 557–574.CrossRefGoogle Scholar
Rewienski, M. & White, J. 2003 A trajectory piecewise-linear approach to model order reduction and fast simulation of nonlinear circuits and micromachined devices. IEEE Trans. Comput.-Aided Des. Integrated Circuits Syst. 22 (2), 155–170.CrossRefGoogle Scholar
Rink, B. 2006 Proof of Nishida’s conjecture on anharmonic lattices. Commun. Math. Phys. 261 (3), 613–627.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.CrossRefGoogle Scholar
Weinstein, A. 1983 Hamiltonian structure for drift waves and geostrophic flow. Phys. Fluids 26 (2), 388–390.CrossRefGoogle Scholar
Wiggins, S. 2003 Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer.Google Scholar