Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T01:42:53.219Z Has data issue: false hasContentIssue false
  • English
  • Français

On the limitation of imposed velocity field strategy for Coulomb-driven electroconvection flow simulations

Published online by Cambridge University Press:  26 June 2013

Philippe Traoré  and
Jian Wu
Philippe Traoré*
Affiliation:
Institut PPRIME, Boulevard Pierre et Marie Curie, BP 30179, 86962 Futuroscope-Chasseneuil, France
Jian Wu
Affiliation:
Institut PPRIME, Boulevard Pierre et Marie Curie, BP 30179, 86962 Futuroscope-Chasseneuil, France
*
†Email address for correspondence: philippe.traore@univ-poitiers.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

This study refers to the article of Chicón, Castellanos & Martion (J. Fluid Mech., vol. 344, 1997, pp. 43–66), who presented a numerical study of electroconvection in a layer of dielectric liquid induced by unipolar injection. An important characteristic of the numerical strategy proposed by Chicón et al. lies in the fact that the Navier–Stokes equations are never solved to obtain the velocity field, which is subsequently needed in the charge density transport equation. Instead, the velocity field is explicitly provided by an expression obtained with some assumptions about the flow structure and related to the electric field (the imposed velocity field approach; IVF). The validity of the above simplification is examined through a direct comparison of the solutions obtained by solving the Navier–Stokes equations (the Navier–Stokes computation approach; NSC). 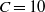It is clearly demonstrated that, even in the strong injection regime ($C= 10$), the results look very similar for a given range of the mobility parameter 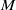$M$; however, in the weak injection regime (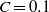$C= 0. 1$), significant discrepancies are observed. The rich flow structures obtained with the NSC approach invalidate the use of the IVF approach in the weak injection regime.

JFM classification

Mathematical Foundations: Computational methods Convection: Convection MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , R3
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atten, P. & Elouadie, L. 1995 EHD convection in a dielectric liquid subjected to unipolar injection: coaxial wire/cylinder geometry. J. Electrostat. 34, 279–297.Google Scholar
Atten, P. & Lacroix, J. C. 1979 Non-linear hydrodynamic stability of liquids subjected to unipolar injection. J. Méc. 18, 469–510.Google Scholar
Atten, P. & Moreau, R. 1972 Stabilité électrohydrodynamique des liquides isolants soumis à une injection unipolaire. J. Méc. 11 (3), 471–521.Google Scholar
Boris, J. P. & Book, D. L. 1973 Flux corrected transport I: a fluid transport algorithm that works. J. Comput. Phys. 11, 38–69.Google Scholar
Castellanos, A. & Atten, P. 1987 Numerical modelling of finite amplitude convection of liquids subjected to unipolar injection. IEEE Trans. Ind. Applics. IA-23, 825–830.Google Scholar
Castellanos, A., Atten, P. & Perez, A. T. 1987 Finite amplitude electroconvection in liquid in the case of weak unipolar injection. Physico-Chem. Hydrodyn. 9 (3/4), 443–452.Google Scholar
Chicón, R., Castellanos, A. & Martion, E. 1997 Numerical modelling of Coulomb-driven convection in insulating liquids. J. Fluid Mech. 344, 43–66.CrossRefGoogle Scholar
Chicón, R., Perez, A. T. & Castellanos, A. 2002 Modelling the finite amplitude electroconvection in cylindrical geometry: characterization of chaos. In Annual Report: Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun 20th–24th October 2002, IEEE conference publications, pp. 212–215.Google Scholar
Chicón, R., Perez, A. T. & Castellanos, A. 2003 Electrovection in small cylindrical cavities. In Annual Report: Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Albuquerque 19th–22th October 2003, IEEE conference publications, pp. 710–713.Google Scholar
Felici, N. 1969 Phénomènes hydro et aérodynamiques dans la conduction des diélectriques fluides. Rev. Gén. Electricité 78, 717–734.Google Scholar
Fortin, M. & Glowinski, R. 1983 Augmented Lagrangian Methods. North-Holland.Google Scholar
Gaskel, P. H. & Lau, A. K. C. 1988 Curvature-compensated convective transport: SMART, a new boundedness-preserving transport algorithm. Intl J. Numer. Meth. Fluids 8, 617–641.Google Scholar
Kourmatzis, A. & Shrimpton, J. S. 2012 Turbulent three-dimensional dielectric electro-hydrodynamic convection between two plates. J. Fluid Mech. 696, 228–262.CrossRefGoogle Scholar
LeVeque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
Patankar, S. V. 1980 Numerical Heat Transfer and Fluid Flow. McGraw-Hill.Google Scholar
Perez, A. T. & Castellanos, A. 1989 Role of charge diffusion in finite-amplitude electroconvection. Phys. Rev. A 40 (10), 5844–5855.Google Scholar
Traoré, P. & Perez, A. T. 2012 Two-dimensional numerical analysis of electroconvection in a dielectric liquid subjected to strong unipolar injection. Phys. Fluids 24, 037102.Google Scholar
Traoré, P., Perez, A. T., Koulova-Nenova, A. D. & Romat, H. 2010 Numerical modelling of finite amplitude electro-thermo-convection in a dielectric liquid layer subjected to both unipolar injection and temperature gradient. J. Fluid Mech. 658, 279–293.Google Scholar
Uzawa, H. 1958 Iterative methods for concave programming. In Studies in Linear and Nonlinear Programming (ed. Arrow, K. J., Hurwicz, L. & Uzawa, H.), pp. 154–165. Stanford University Press.Google Scholar
Vazquez, P. A. & Castellanos, A. 2011 Stability analysis of the 3D electroconvective charged flow between parallel plates using the particle-in-cell method. In IEEE International Conference on Dielectric Liquids (ICDL), Throndheim 26th–30th June 2011, pp. 1–4.Google Scholar
Vazquez, P. A., Georghiou, G. E. & Castellanos, A. 2006 Characterization of injection instabilities in electrohydrodynamics by numerical modelling: comparison of particle in cell and flux corrected transport methods for electroconvection between two plates. J. Phys. D: Appl. Phys. 39, 2754–2763.Google Scholar
Vazquez, P. A., Georghiou, G. E. & Castellanos, A. 2008 Numerical analysis of the stability of the electro-hydrodynamic (EHD) electroconvection between two plates. J. Phys. D: Appl. Phys. 41, 1–10.Google Scholar