Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T20:41:10.797Z Has data issue: false hasContentIssue false
  • English
  • Français

On the periodic injection of fluid into, and its extraction from, a porous medium for seasonal heat storage

Published online by Cambridge University Press:  26 July 2012

Peter Dudfield  and
Andrew W. Woods
Peter Dudfield*
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email addresses for correspondence: peter.dudfield@bpi.cam.ac.uk, andy@bpi.cam.ac.uk
†Email addresses for correspondence: peter.dudfield@bpi.cam.ac.uk, andy@bpi.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the oscillatory motion of fluid which spreads under gravity along a horizontal impermeable boundary through a porous medium controlled by the periodic injection and extraction of fluid from a horizontal well. Over the first few cycles the volume of injected fluid exceeds that which is extracted owing to the gravitational spreading of the current. However, after many cycles, these volumes converge and the flow develops into two regions. Near the source there is a zone 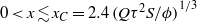in which the depth of the fluid varies periodically with each cycle, where 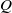is the fluid injection rate, is the injection or extraction time, 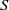is the speed of the buoyancy-driven flow and 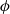is the porosity. The current attains its maximum depth, 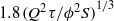at the source, where the minimum depth equals zero. At long times, the current depth at 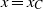is approximately constant, 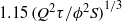, and beyond this point, the current spreads horizontally, driven by an effective flux 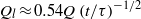, so that the length of the current increases as 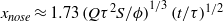. We confirm these predictions with new experiments using a Hele-Shaw cell. We also model the evolution of the thermal front which develops if the injected fluid is hotter than the formation temperature. We find conditions under which all the extracted fluid is hot but owing to the mismatch between the volume of injected and extracted fluids, not all the injected thermal energy is recovered, and the surrounding rock heats up.

JFM classification

Convection: Convection in porous media Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 467 - 481
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ames, W. F. 1965 Nonlinear Partial Differential Equations in Engineering. Academic.Google Scholar
2. Barenblatt, G. I. 1996 Scaling, Self-Similarity, and Intermediate Asymptotics. Cambridge University Press.Google Scholar
3. Barenblatt, G. I., Entov, V. M. & Ryzhik, V. M. 1990 Theory of Fluid Flows through Natural Rocks. Kluwer.Google Scholar
4. Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
5. Bolster, D., Dentz, M. & Carrera, J. 2009 Effective two-phase flow in heterogeneous media under temporal pressure fluctuations. Water Resour. Res. 45, W05408.Google Scholar
6. Dentz, M. & Carrera, J. 2005 Effective solute transport in temporally fluctuating flow through heterogeneous media. Water Resour. Res. 41, W08414.Google Scholar
7. de Dreuzy, J.-R., Carrera, J., Dentz, M. & Le Borgne, T. 2012 Asymptotic dispersion for two-dimensional highly heterogeneous permeability fields under temporally fluctuating flow. Water Resour. Res. 48, W01532.Google Scholar
8. Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
9. Lake, L. W. 1996 Enhanced Oil Recovery. Prentice-Hall.Google Scholar
10. Lide, D. R. 2001 CRC Handbook of Chemistry and Physics, 82nd edn. CRC.Google Scholar
11. Mackay, D. J. C. 2008 Sustainable Energy – Without the Hot Air. UIT Cambridge.Google Scholar
12. Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.CrossRefGoogle Scholar
13. Nordbotten, J. & Celia, M. 2006 Similarity solutions for fluid injections into confined aquifers. J. Fluid Mech. 561, 307–327.Google Scholar
14. Phillips, O. M. 1991 Flow and Reactions in Permeable Rocks. Cambridge University Press.Google Scholar
15. Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.Google Scholar
16. Raw, A. V. W. & Woods, A. W. 2003 On gravity-driven flow through a reacting porous rock. J. Fluid Mech. 474, 227–472.Google Scholar
17. Woods, A. W 1999 Liquid and vapour flow in superheated rock. Annu. Rev. Fluid Mech. 31, 171–199.Google Scholar
18. Woods, A. W & Fitzgerald, S. D. 1993 The vaporization of a liquid front moving through a hot porous rock. J. Fluid Mech. 251, 563–579.Google Scholar