Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Weipeng
Fan, Yitong
Modesti, Davide
and
Cheng, Cheng
2019.
Decomposition of the mean skin-friction drag in compressible turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
101.
Modesti, Davide
Pirozzoli, Sergio
and
Grasso, Francesco
2019.
Direct numerical simulation of developed compressible flow in square ducts.
International Journal of Heat and Fluid Flow,
Vol. 76,
Issue. ,
p.
130.
Fan, Yitong
Li, Weipeng
and
Pirozzoli, Sergio
2019.
Decomposition of the mean friction drag in zero-pressure-gradient turbulent boundary layers.
Physics of Fluids,
Vol. 31,
Issue. 8,
Wang, Yanzhi
Zhao, Yanlin
and
Yao, Jun
2019.
Particle dispersion in turbulent, square open duct flows of high Reynolds number.
Powder Technology,
Vol. 354,
Issue. ,
p.
92.
Klein, Marten
Zenker, Christian
and
Schmidt, Heiko
2019.
Small-scale resolving simulations of the turbulent mixing in confined planar jets using one-dimensional turbulence.
Chemical Engineering Science,
Vol. 204,
Issue. ,
p.
186.
Gallegos, Ralph Kristoffer B.
and
Sharma, Rajnish N.
2019.
Heat transfer performance of flag vortex generators in rectangular channels.
International Journal of Thermal Sciences,
Vol. 137,
Issue. ,
p.
26.
Nikora, V. I.
Stoesser, T.
Cameron, S. M.
Stewart, M.
Papadopoulos, K.
Ouro, P.
McSherry, R.
Zampiron, A.
Marusic, I.
and
Falconer, R. A.
2019.
Friction factor decomposition for rough-wall flows: theoretical background and application to open-channel flows.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
626.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
Fan, Yitong
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012010.
Yang, Rui
Wang, Zhen-guo
Zhao, Yu-xin
Wang, Qian-cheng
and
Feng, Wu-heng
2020.
Numerical investigation on spatial development of the secondary flow in a supersonic turbulent square duct.
Aerospace Science and Technology,
Vol. 100,
Issue. ,
p.
105832.
Khan, Hamid Hassan
Anwer, Syed Fahad
Hasan, Nadeem
and
Sanghi, Sanjeev
2020.
The organized motion of characterized turbulent flow at low Reynolds number in a straight square duct.
SN Applied Sciences,
Vol. 2,
Issue. 4,
Modesti, Davide
2020.
A priori tests of eddy viscosity models in square duct flow.
Theoretical and Computational Fluid Dynamics,
Vol. 34,
Issue. 5-6,
p.
713.
Fan, Yitong
Li, Weipeng
and
Pirozzoli, Sergio
2020.
Energy-based decomposition of friction drag in turbulent square-duct flows.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108731.
Cheng, Cheng
Li, Weipeng
Lozano-Durán, Adrián
and
Liu, Hong
2020.
On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Yang, Run-ze
Yang, Rui
and
Zhao, Yu-xin
2021.
Influence of compressibility on the development of streamwise supersonic corner flow.
Physics of Fluids,
Vol. 33,
Issue. 11,
Duan, Yanchong
Zhong, Qiang
Wang, Guiquan
Zhang, Peng
and
Li, Danxun
2021.
Contributions of different scales of turbulent motions to the mean wall-shear stress in open channel flows at low-to-moderate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Modesti, Davide
Endrikat, Sebastian
Hutchins, Nicholas
and
Chung, Daniel
2021.
Dispersive stresses in turbulent flow over riblets.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Atzori, Marco
Vinuesa, Ricardo
Lozano-Durán, Adrián
and
Schlatter, Philipp
2021.
Intense Reynolds-stress events in turbulent ducts.
International Journal of Heat and Fluid Flow,
Vol. 89,
Issue. ,
p.
108802.
Zhao, Yanlin
Wang, Yanzhi
and
Yao, Jun
2021.
Effect of turbulence-driven secondary flow on particle preferential concentration and clustering in turbulent square duct flows.
Particuology,
Vol. 55,
Issue. ,
p.
70.
Yang, Rui
Modesti, Davide
Zhao, Yu-xin
Wang, Qian-cheng
Wang, Zhen-guo
and
Pirozzoli, Sergio
2021.
Influence of corner angle in streamwise supersonic corner flow.
Physics of Fluids,
Vol. 33,
Issue. 5,
Wangsawijaya, D.D.
and
Hutchins, N.
2022.
Investigation of unsteady secondary flows and large-scale turbulence in heterogeneous turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
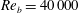 $Re_{b}=40\,000$ to quantitatively analyse the role of secondary motions on the mean flow structure. For that purpose we derive a generalized form of the identity of Fukagata, Iwamoto and Kasagi (FIK), which allows one to quantify the effect of cross-stream convection on the mean streamwise velocity, wall shear stress and bulk friction coefficient. Secondary motions are found to contribute approximately 6 % of the total friction, and to act as a self-regulating mechanism of turbulence whereby wall shear stress non-uniformities induced by corners are equalized, and universality of the wall-normal velocity profiles is established. We also carry out numerical experiments whereby the secondary motions are artificially suppressed, in which case their equalizing role is partially taken by the turbulent stresses.
$Re_{b}=40\,000$ to quantitatively analyse the role of secondary motions on the mean flow structure. For that purpose we derive a generalized form of the identity of Fukagata, Iwamoto and Kasagi (FIK), which allows one to quantify the effect of cross-stream convection on the mean streamwise velocity, wall shear stress and bulk friction coefficient. Secondary motions are found to contribute approximately 6 % of the total friction, and to act as a self-regulating mechanism of turbulence whereby wall shear stress non-uniformities induced by corners are equalized, and universality of the wall-normal velocity profiles is established. We also carry out numerical experiments whereby the secondary motions are artificially suppressed, in which case their equalizing role is partially taken by the turbulent stresses.


