Published online by Cambridge University Press: 16 April 2018
Experiments are performed to characterize the onset of laminar–turbulent transition in the flow of high-molecular-weight polymer solutions in rigid microtubes of diameters in the range 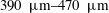 $390~\unicode[STIX]{x03BC}\text{m}{-}470~\unicode[STIX]{x03BC}\text{m}$ using the micro-PIV technique. By considering flow in tubes of such small diameters, the present study probes higher values of elasticity numbers (
$390~\unicode[STIX]{x03BC}\text{m}{-}470~\unicode[STIX]{x03BC}\text{m}$ using the micro-PIV technique. By considering flow in tubes of such small diameters, the present study probes higher values of elasticity numbers (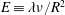 $E\equiv \unicode[STIX]{x1D706}\unicode[STIX]{x1D708}/R^{2}$) compared to existing studies, where
$E\equiv \unicode[STIX]{x1D706}\unicode[STIX]{x1D708}/R^{2}$) compared to existing studies, where 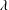 $\unicode[STIX]{x1D706}$ is the longest relaxation time of the polymer solution,
$\unicode[STIX]{x1D706}$ is the longest relaxation time of the polymer solution, 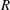 $R$ is the tube radius and
$R$ is the tube radius and  $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the polymer solution. For the Newtonian case, our experiments indicate that the natural transition (without the aid of any forcing mechanism) occurs at Reynolds number (
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of the polymer solution. For the Newtonian case, our experiments indicate that the natural transition (without the aid of any forcing mechanism) occurs at Reynolds number (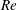 $Re$)
$Re$) 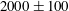 $2000\pm 100$. As the concentration of polymer is increased, initially there is a delay in the onset of the transition and the transition Reynolds number increases to
$2000\pm 100$. As the concentration of polymer is increased, initially there is a delay in the onset of the transition and the transition Reynolds number increases to 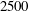 $2500$. Further increase in concentration of the polymer results in a decrease in the Reynolds number for transition. At sufficiently high concentrations, the added polymer tends to destabilize the flow and the transition is observed to happen at
$2500$. Further increase in concentration of the polymer results in a decrease in the Reynolds number for transition. At sufficiently high concentrations, the added polymer tends to destabilize the flow and the transition is observed to happen at 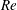 $Re$ as low as
$Re$ as low as 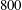 $800$. It is also observed that the addition of polymers, regardless of their concentration, reduces the magnitude of the velocity fluctuations after transition. Dye-stream visualization is further used to corroborate the onset of transition in the flow of polymer solutions. The present work thus shows that addition of polymer, at sufficiently high concentrations, destabilizes the flow when compared to that of a Newtonian fluid, thereby providing additional evidence for ‘early transition’ or ‘elasto-inertial turbulence’ in the flow of polymer solutions. The data for the transition Reynolds number
$800$. It is also observed that the addition of polymers, regardless of their concentration, reduces the magnitude of the velocity fluctuations after transition. Dye-stream visualization is further used to corroborate the onset of transition in the flow of polymer solutions. The present work thus shows that addition of polymer, at sufficiently high concentrations, destabilizes the flow when compared to that of a Newtonian fluid, thereby providing additional evidence for ‘early transition’ or ‘elasto-inertial turbulence’ in the flow of polymer solutions. The data for the transition Reynolds number 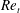 $Re_{t}$ from our experiments (for tubes of different diameters, and for two different polymers at varying concentrations) collapse well according to the scaling relation
$Re_{t}$ from our experiments (for tubes of different diameters, and for two different polymers at varying concentrations) collapse well according to the scaling relation 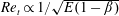 $Re_{t}\propto 1/\sqrt{E(1-\unicode[STIX]{x1D6FD})}$, where
$Re_{t}\propto 1/\sqrt{E(1-\unicode[STIX]{x1D6FD})}$, where 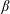 $\unicode[STIX]{x1D6FD}$ is the ratio of solvent viscosity to the viscosity of the polymer solution.
$\unicode[STIX]{x1D6FD}$ is the ratio of solvent viscosity to the viscosity of the polymer solution.