1. Introduction
On a list of the most studied fluid mechanics problems, the flow around a circular cylinder would surely be at the top end. The cylinder is the prototype bluff body, and the flow around it has been used to gain insight into separated flows, their stability and ways to control them.
The flow in an unbounded domain depends on a single dimensionless parameter, the Reynolds number  $Re=UD/\nu$, where
$Re=UD/\nu$, where  $U$ is the incoming fluid velocity,
$U$ is the incoming fluid velocity,  $D$ is the diameter of the cylinder and
$D$ is the diameter of the cylinder and  $\nu$ is the kinematic viscosity of the fluid. The most fundamental instability occurs at
$\nu$ is the kinematic viscosity of the fluid. The most fundamental instability occurs at  $Re_H \approx 46$, where the symmetric steady flow becomes unstable, and a periodic flow appears (Williamson Reference Williamson1996). The periodic flow leads to vortex shedding, giving rise to the famous Kármán vortex street where vortices of alternate signs are shed from the cylinder. In terms of bifurcation theory, the transition is a supercritical Hopf bifurcation (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987).
$Re_H \approx 46$, where the symmetric steady flow becomes unstable, and a periodic flow appears (Williamson Reference Williamson1996). The periodic flow leads to vortex shedding, giving rise to the famous Kármán vortex street where vortices of alternate signs are shed from the cylinder. In terms of bifurcation theory, the transition is a supercritical Hopf bifurcation (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987).
If the cylinder also rotates, another dimensionless parameter appears,  $\alpha = \varOmega D/2U$, where
$\alpha = \varOmega D/2U$, where  $\varOmega$ is the angular velocity of the cylinder. The rotation breaks the symmetry of the steady solution and stabilizes it, such that the critical Reynolds number
$\varOmega$ is the angular velocity of the cylinder. The rotation breaks the symmetry of the steady solution and stabilizes it, such that the critical Reynolds number  $Re_H$ increases rapidly with
$Re_H$ increases rapidly with  $\alpha$ in the range
$\alpha$ in the range  $0 < \alpha < 2$, see figure 1.
$0 < \alpha < 2$, see figure 1.
Figure 1. Bifurcations diagram showing curves of elementary bifurcations in the  $(Re,\alpha )$ parameter plane. Boxes to the right show streamlines and vorticity at the bifurcation points for
$(Re,\alpha )$ parameter plane. Boxes to the right show streamlines and vorticity at the bifurcation points for  $Re=200$. Full lines denote Hopf bifurcations, dashed and dash-dotted lines are fold bifurcations. There are three steady states in the grey region. Mode I is the periodic Kármán wake; mode II is the low-frequency periodic flow; TB-C marks a Takens–Bogdanov point and a cusp that are very close; GH is a generalized Hopf point which will not be discussed here. From Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020).
$Re=200$. Full lines denote Hopf bifurcations, dashed and dash-dotted lines are fold bifurcations. There are three steady states in the grey region. Mode I is the periodic Kármán wake; mode II is the low-frequency periodic flow; TB-C marks a Takens–Bogdanov point and a cusp that are very close; GH is a generalized Hopf point which will not be discussed here. From Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020).
For higher values of  $\alpha$ a more complex scenario occurs. Low-frequency periodic solutions (denoted mode II) with shedding of same-sign vortices have been found (Stojković, Breuer & Durst Reference Stojković, Breuer and Durst2002), as well as a range with up to three steady states (Pralits, Brandt & Gianetti Reference Pralits, Brandt and Gianetti2010; Rao et al. Reference Rao, Leontini, Thompson and Hourigan2013).
$\alpha$ a more complex scenario occurs. Low-frequency periodic solutions (denoted mode II) with shedding of same-sign vortices have been found (Stojković, Breuer & Durst Reference Stojković, Breuer and Durst2002), as well as a range with up to three steady states (Pralits, Brandt & Gianetti Reference Pralits, Brandt and Gianetti2010; Rao et al. Reference Rao, Leontini, Thompson and Hourigan2013).
Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) give for the first time a complete description of the intricate pattern of bifurcations that connect these states under variation of  $Re$ and
$Re$ and  $\alpha$. The important insight is that the bifurcation diagram can be understood from an organizing centre, a state with highly degenerate dynamics. The organizing centre has codimension three, meaning that three parameters are needed to realize all possible kinds of dynamics near it. This is surprising, as the system at hand only has two parameters, and the dynamics of the organizing centre cannot be realized for the physical system. Nevertheless, this ‘super’ organizing centre is a most useful mathematical abstraction which Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) use as a guide to conjecture the structure of the physical bifurcation diagram and verify it by numerical simulations.
$\alpha$. The important insight is that the bifurcation diagram can be understood from an organizing centre, a state with highly degenerate dynamics. The organizing centre has codimension three, meaning that three parameters are needed to realize all possible kinds of dynamics near it. This is surprising, as the system at hand only has two parameters, and the dynamics of the organizing centre cannot be realized for the physical system. Nevertheless, this ‘super’ organizing centre is a most useful mathematical abstraction which Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) use as a guide to conjecture the structure of the physical bifurcation diagram and verify it by numerical simulations.
2. Overview
A two-parameter bifurcation diagram is built up by a number of curves of elementary bifurcations. For the rotating cylinder, curves of Hopf bifurcations and fold (saddle-node) bifurcations occur. In a fold bifurcation two steady states, one stable, one unstable, appear out of the blue. The bifurcation curves can meet in special singularities, codimension-two points, also denoted organizing centres (Golubitsky & Schaeffer Reference Golubitsky and Schaeffer1985). By analysing simple representative cases, normal forms, the qualitative structure of the bifurcation diagram near a codimension-two singularity can be found (Kuznetsov Reference Kuznetsov2004).
Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) argue that two codimension-two singularities are relevant for the rotating cylinder. One is the cusp, where two fold curves meet. Close to a cusp up to three steady states can be present. The other is the Takens–Bogdanov (TB) point, where a Hopf curve and a fold curve meet. From a TB point a curve of homoclinic bifurcations also emanates. In these bifurcations a periodic state disappears as the frequency tends to zero. This fits well with the low-frequency mode II periodic flows. Neither the cusp nor the TB point alone can account for all the available observations. Both will be needed for a complete description.
Figure 1 show the curves of elementary bifurcations computed by Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020). As anticipated, both a cusp and a TB point are found. The two points are very close,  $(Re,\alpha ) = (75.6, 5.38)$ and
$(Re,\alpha ) = (75.6, 5.38)$ and  $(77.6, 5.36)$, respectively. This indicates that a small change of the dynamical system at hand could make the two points merge into a more degenerate singularity. Such a degenerate TB point has codimension three and the corresponding local bifurcation diagram has three parameters. The bifurcation diagram has been determined for a normal form by Dumortier et al. (Reference Dumortier, Roussarie, Sotomayor and Zoladec1991), and it is expected that the bifurcation diagram for the rotating cylinder will correspond to a two-dimensional slice in the extended three-dimensional parameter space. A candidate for such a slice is shown in figure 2. As required, it includes both a cusp and a TB point, but there is an additional organizing centre, a saddle-node loop. At this point the dynamics exhibits a fold bifurcation point on a limit cycle, and in the bifurcation diagram a curve of homoclinic bifurcations emanates which ends at the TB point. By careful simulations, Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) confirm that all the features of figure 2 are indeed present for the rotating cylinder. However, on the scale of figure 1 the details of figure 2 are too fine to be seen. Hence, the organizing centres and the bifurcation curves joining them in the two-dimensional
$(77.6, 5.36)$, respectively. This indicates that a small change of the dynamical system at hand could make the two points merge into a more degenerate singularity. Such a degenerate TB point has codimension three and the corresponding local bifurcation diagram has three parameters. The bifurcation diagram has been determined for a normal form by Dumortier et al. (Reference Dumortier, Roussarie, Sotomayor and Zoladec1991), and it is expected that the bifurcation diagram for the rotating cylinder will correspond to a two-dimensional slice in the extended three-dimensional parameter space. A candidate for such a slice is shown in figure 2. As required, it includes both a cusp and a TB point, but there is an additional organizing centre, a saddle-node loop. At this point the dynamics exhibits a fold bifurcation point on a limit cycle, and in the bifurcation diagram a curve of homoclinic bifurcations emanates which ends at the TB point. By careful simulations, Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) confirm that all the features of figure 2 are indeed present for the rotating cylinder. However, on the scale of figure 1 the details of figure 2 are too fine to be seen. Hence, the organizing centres and the bifurcation curves joining them in the two-dimensional  $(Re,\alpha )$ plane are themselves organized from a ‘super’ organizing centre, the degenerate TB point.
$(Re,\alpha )$ plane are themselves organized from a ‘super’ organizing centre, the degenerate TB point.
3. Future
The question naturally arises if the setting of the problem could be modified such that a third parameter appears, and the degenerate TB point could be realized physically. Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) suggest considering compressibility, or changing the external boundary conditions by confinement or shear in the incoming flow. If such attempts were successful, the full three-parameter diagram of the degenerate TB bifurcation could be realized, and bifurcation diagrams different from figure 2, corresponding to different slices in the three-dimensional parameter space, would occur. If the third parameter is sufficiently large, the bifurcation diagram in figure 2 could occupy a substantially larger part of the  $(Re,\alpha )$ space and be experimentally observable.
$(Re,\alpha )$ space and be experimentally observable.
It would be interesting to understand better why the flow around a rotating cylinder is so close to a codimension-three singularity. The rotating cylinder is unique in the sense that the boundary is time independent, and steady flows are allowed. This is not the case for any other rotating shape. Is there a hidden symmetry?
The approach of Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) will be useful in other similar problems. What is required is a problem that is relatively simple from a dynamical point of view, that is, only steady states and periodic flows occur, but which has complex dependence on parameters. Many two-dimensional flows at low  $Re$ will fit in this category.
$Re$ will fit in this category.
Declaration of interest
The author reports no conflict of interest.

 $(Re,\alpha )$ parameter plane. Boxes to the right show streamlines and vorticity at the bifurcation points for
$(Re,\alpha )$ parameter plane. Boxes to the right show streamlines and vorticity at the bifurcation points for  $Re=200$. Full lines denote Hopf bifurcations, dashed and dash-dotted lines are fold bifurcations. There are three steady states in the grey region. Mode I is the periodic Kármán wake; mode II is the low-frequency periodic flow; TB-C marks a Takens–Bogdanov point and a cusp that are very close; GH is a generalized Hopf point which will not be discussed here. From Sierra et al. (2020).
$Re=200$. Full lines denote Hopf bifurcations, dashed and dash-dotted lines are fold bifurcations. There are three steady states in the grey region. Mode I is the periodic Kármán wake; mode II is the low-frequency periodic flow; TB-C marks a Takens–Bogdanov point and a cusp that are very close; GH is a generalized Hopf point which will not be discussed here. From Sierra et al. (2020).
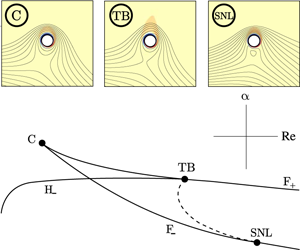
 $C$, cusp bifurcation; TB, Takens–Bogdanov point; SNL, saddle-node-loop point;
$C$, cusp bifurcation; TB, Takens–Bogdanov point; SNL, saddle-node-loop point;  $H_-$, Hopf bifurcation curve;
$H_-$, Hopf bifurcation curve;  $F_+, F_-$, fold bifurcation curves;
$F_+, F_-$, fold bifurcation curves;  $H_{\infty }$, homoclinic bifurcation curve. Typical dynamics in each sector are shown in the boxes. Boxes with yellow background show streamlines and vorticity at the codimension-two points. From Sierra et al. (2020).
$H_{\infty }$, homoclinic bifurcation curve. Typical dynamics in each sector are shown in the boxes. Boxes with yellow background show streamlines and vorticity at the codimension-two points. From Sierra et al. (2020).



1. Introduction
On a list of the most studied fluid mechanics problems, the flow around a circular cylinder would surely be at the top end. The cylinder is the prototype bluff body, and the flow around it has been used to gain insight into separated flows, their stability and ways to control them.
The flow in an unbounded domain depends on a single dimensionless parameter, the Reynolds number $Re=UD/\nu$, where
$Re=UD/\nu$, where  $U$ is the incoming fluid velocity,
$U$ is the incoming fluid velocity,  $D$ is the diameter of the cylinder and
$D$ is the diameter of the cylinder and  $\nu$ is the kinematic viscosity of the fluid. The most fundamental instability occurs at
$\nu$ is the kinematic viscosity of the fluid. The most fundamental instability occurs at  $Re_H \approx 46$, where the symmetric steady flow becomes unstable, and a periodic flow appears (Williamson Reference Williamson1996). The periodic flow leads to vortex shedding, giving rise to the famous Kármán vortex street where vortices of alternate signs are shed from the cylinder. In terms of bifurcation theory, the transition is a supercritical Hopf bifurcation (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987).
$Re_H \approx 46$, where the symmetric steady flow becomes unstable, and a periodic flow appears (Williamson Reference Williamson1996). The periodic flow leads to vortex shedding, giving rise to the famous Kármán vortex street where vortices of alternate signs are shed from the cylinder. In terms of bifurcation theory, the transition is a supercritical Hopf bifurcation (Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987).
If the cylinder also rotates, another dimensionless parameter appears, $\alpha = \varOmega D/2U$, where
$\alpha = \varOmega D/2U$, where  $\varOmega$ is the angular velocity of the cylinder. The rotation breaks the symmetry of the steady solution and stabilizes it, such that the critical Reynolds number
$\varOmega$ is the angular velocity of the cylinder. The rotation breaks the symmetry of the steady solution and stabilizes it, such that the critical Reynolds number  $Re_H$ increases rapidly with
$Re_H$ increases rapidly with  $\alpha$ in the range
$\alpha$ in the range  $0 < \alpha < 2$, see figure 1.
$0 < \alpha < 2$, see figure 1.
Figure 1. Bifurcations diagram showing curves of elementary bifurcations in the $(Re,\alpha )$ parameter plane. Boxes to the right show streamlines and vorticity at the bifurcation points for
$(Re,\alpha )$ parameter plane. Boxes to the right show streamlines and vorticity at the bifurcation points for  $Re=200$. Full lines denote Hopf bifurcations, dashed and dash-dotted lines are fold bifurcations. There are three steady states in the grey region. Mode I is the periodic Kármán wake; mode II is the low-frequency periodic flow; TB-C marks a Takens–Bogdanov point and a cusp that are very close; GH is a generalized Hopf point which will not be discussed here. From Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020).
$Re=200$. Full lines denote Hopf bifurcations, dashed and dash-dotted lines are fold bifurcations. There are three steady states in the grey region. Mode I is the periodic Kármán wake; mode II is the low-frequency periodic flow; TB-C marks a Takens–Bogdanov point and a cusp that are very close; GH is a generalized Hopf point which will not be discussed here. From Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020).
For higher values of $\alpha$ a more complex scenario occurs. Low-frequency periodic solutions (denoted mode II) with shedding of same-sign vortices have been found (Stojković, Breuer & Durst Reference Stojković, Breuer and Durst2002), as well as a range with up to three steady states (Pralits, Brandt & Gianetti Reference Pralits, Brandt and Gianetti2010; Rao et al. Reference Rao, Leontini, Thompson and Hourigan2013).
$\alpha$ a more complex scenario occurs. Low-frequency periodic solutions (denoted mode II) with shedding of same-sign vortices have been found (Stojković, Breuer & Durst Reference Stojković, Breuer and Durst2002), as well as a range with up to three steady states (Pralits, Brandt & Gianetti Reference Pralits, Brandt and Gianetti2010; Rao et al. Reference Rao, Leontini, Thompson and Hourigan2013).
Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) give for the first time a complete description of the intricate pattern of bifurcations that connect these states under variation of $Re$ and
$Re$ and  $\alpha$. The important insight is that the bifurcation diagram can be understood from an organizing centre, a state with highly degenerate dynamics. The organizing centre has codimension three, meaning that three parameters are needed to realize all possible kinds of dynamics near it. This is surprising, as the system at hand only has two parameters, and the dynamics of the organizing centre cannot be realized for the physical system. Nevertheless, this ‘super’ organizing centre is a most useful mathematical abstraction which Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) use as a guide to conjecture the structure of the physical bifurcation diagram and verify it by numerical simulations.
$\alpha$. The important insight is that the bifurcation diagram can be understood from an organizing centre, a state with highly degenerate dynamics. The organizing centre has codimension three, meaning that three parameters are needed to realize all possible kinds of dynamics near it. This is surprising, as the system at hand only has two parameters, and the dynamics of the organizing centre cannot be realized for the physical system. Nevertheless, this ‘super’ organizing centre is a most useful mathematical abstraction which Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) use as a guide to conjecture the structure of the physical bifurcation diagram and verify it by numerical simulations.
2. Overview
A two-parameter bifurcation diagram is built up by a number of curves of elementary bifurcations. For the rotating cylinder, curves of Hopf bifurcations and fold (saddle-node) bifurcations occur. In a fold bifurcation two steady states, one stable, one unstable, appear out of the blue. The bifurcation curves can meet in special singularities, codimension-two points, also denoted organizing centres (Golubitsky & Schaeffer Reference Golubitsky and Schaeffer1985). By analysing simple representative cases, normal forms, the qualitative structure of the bifurcation diagram near a codimension-two singularity can be found (Kuznetsov Reference Kuznetsov2004).
Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) argue that two codimension-two singularities are relevant for the rotating cylinder. One is the cusp, where two fold curves meet. Close to a cusp up to three steady states can be present. The other is the Takens–Bogdanov (TB) point, where a Hopf curve and a fold curve meet. From a TB point a curve of homoclinic bifurcations also emanates. In these bifurcations a periodic state disappears as the frequency tends to zero. This fits well with the low-frequency mode II periodic flows. Neither the cusp nor the TB point alone can account for all the available observations. Both will be needed for a complete description.
Figure 1 show the curves of elementary bifurcations computed by Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020). As anticipated, both a cusp and a TB point are found. The two points are very close, $(Re,\alpha ) = (75.6, 5.38)$ and
$(Re,\alpha ) = (75.6, 5.38)$ and  $(77.6, 5.36)$, respectively. This indicates that a small change of the dynamical system at hand could make the two points merge into a more degenerate singularity. Such a degenerate TB point has codimension three and the corresponding local bifurcation diagram has three parameters. The bifurcation diagram has been determined for a normal form by Dumortier et al. (Reference Dumortier, Roussarie, Sotomayor and Zoladec1991), and it is expected that the bifurcation diagram for the rotating cylinder will correspond to a two-dimensional slice in the extended three-dimensional parameter space. A candidate for such a slice is shown in figure 2. As required, it includes both a cusp and a TB point, but there is an additional organizing centre, a saddle-node loop. At this point the dynamics exhibits a fold bifurcation point on a limit cycle, and in the bifurcation diagram a curve of homoclinic bifurcations emanates which ends at the TB point. By careful simulations, Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) confirm that all the features of figure 2 are indeed present for the rotating cylinder. However, on the scale of figure 1 the details of figure 2 are too fine to be seen. Hence, the organizing centres and the bifurcation curves joining them in the two-dimensional
$(77.6, 5.36)$, respectively. This indicates that a small change of the dynamical system at hand could make the two points merge into a more degenerate singularity. Such a degenerate TB point has codimension three and the corresponding local bifurcation diagram has three parameters. The bifurcation diagram has been determined for a normal form by Dumortier et al. (Reference Dumortier, Roussarie, Sotomayor and Zoladec1991), and it is expected that the bifurcation diagram for the rotating cylinder will correspond to a two-dimensional slice in the extended three-dimensional parameter space. A candidate for such a slice is shown in figure 2. As required, it includes both a cusp and a TB point, but there is an additional organizing centre, a saddle-node loop. At this point the dynamics exhibits a fold bifurcation point on a limit cycle, and in the bifurcation diagram a curve of homoclinic bifurcations emanates which ends at the TB point. By careful simulations, Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) confirm that all the features of figure 2 are indeed present for the rotating cylinder. However, on the scale of figure 1 the details of figure 2 are too fine to be seen. Hence, the organizing centres and the bifurcation curves joining them in the two-dimensional  $(Re,\alpha )$ plane are themselves organized from a ‘super’ organizing centre, the degenerate TB point.
$(Re,\alpha )$ plane are themselves organized from a ‘super’ organizing centre, the degenerate TB point.
Figure 2. A two-dimensional slice through the three-dimensional bifurcation diagram of the degenerate Takens–Bogdanov bifurcation. Here $C$, cusp bifurcation; TB, Takens–Bogdanov point; SNL, saddle-node-loop point;
$C$, cusp bifurcation; TB, Takens–Bogdanov point; SNL, saddle-node-loop point;  $H_-$, Hopf bifurcation curve;
$H_-$, Hopf bifurcation curve;  $F_+, F_-$, fold bifurcation curves;
$F_+, F_-$, fold bifurcation curves;  $H_{\infty }$, homoclinic bifurcation curve. Typical dynamics in each sector are shown in the boxes. Boxes with yellow background show streamlines and vorticity at the codimension-two points. From Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020).
$H_{\infty }$, homoclinic bifurcation curve. Typical dynamics in each sector are shown in the boxes. Boxes with yellow background show streamlines and vorticity at the codimension-two points. From Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020).
3. Future
The question naturally arises if the setting of the problem could be modified such that a third parameter appears, and the degenerate TB point could be realized physically. Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) suggest considering compressibility, or changing the external boundary conditions by confinement or shear in the incoming flow. If such attempts were successful, the full three-parameter diagram of the degenerate TB bifurcation could be realized, and bifurcation diagrams different from figure 2, corresponding to different slices in the three-dimensional parameter space, would occur. If the third parameter is sufficiently large, the bifurcation diagram in figure 2 could occupy a substantially larger part of the $(Re,\alpha )$ space and be experimentally observable.
$(Re,\alpha )$ space and be experimentally observable.
It would be interesting to understand better why the flow around a rotating cylinder is so close to a codimension-three singularity. The rotating cylinder is unique in the sense that the boundary is time independent, and steady flows are allowed. This is not the case for any other rotating shape. Is there a hidden symmetry?
The approach of Sierra et al. (Reference Sierra, Fabre, Citro and Giannetti2020) will be useful in other similar problems. What is required is a problem that is relatively simple from a dynamical point of view, that is, only steady states and periodic flows occur, but which has complex dependence on parameters. Many two-dimensional flows at low $Re$ will fit in this category.
$Re$ will fit in this category.
Declaration of interest
The author reports no conflict of interest.