Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T13:40:13.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillations in cylinder wakes at Mach 4

Published online by Cambridge University Press:  23 November 2015

B. E. Schmidt Open the ORCID record for B. E. Schmidt [Opens in a new window]  and
J. E. Shepherd
B. E. Schmidt*
Affiliation:
Department of Aerospace Engineering, California Institute of Technology, Pasadena, CA 91101, USA
J. E. Shepherd
Affiliation:
Department of Aerospace Engineering, California Institute of Technology, Pasadena, CA 91101, USA
*
†Email address for correspondence: bryan.e.schmidt@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

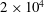The wake behind a circular cylinder in Mach 4 flow is examined experimentally in the Reynolds number range $2\times 10^{4}$ to 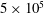$5\times 10^{5}$. Periodic oscillations of the sliplines in the wake are observed. The Strouhal number of the oscillations based on the diameter of the cylinder is found to increase monotonically from 0.30 to 0.50 with increasing Reynolds number. If the Strouhal number is formed using the length of the sliplines, however, it has a constant value of approximately 0.48 for all Reynolds numbers studied. This scaling indicates that the oscillations in supersonic flow are likely driven by acoustic signals propagating back and forth through the subsonic region between the separation points on the cylinder and the neck where the sliplines converge, unlike in subsonic flow where oscillations are caused by vortices shed from the cylinder surface.

JFM classification

Aerodynamics: Aerodynamics Aerodynamics: High-speed flow Wakes/Jets: Wakes
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 785 , 25 December 2015 , R3
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bashkin, V. A., Egorov, I. V., Egorova, M. V. & Ivanov, D. V. 1998 Initiation and development of separated flow behind a circular cylinder in a supersonic stream. Fluid Dyn. 33 (6), 833–841.Google Scholar
Bashkin, V. A., Egorov, I. V., Egorova, M. V. & Ivanov, D. V. 2000 Supersonic laminar-turbulent gas flow past a circular cylinder. Fluid Dyn. 35 (5), 652–662.CrossRefGoogle Scholar
Bashkin, V. A., Vaganov, A. V., Egorov, I. V., Ivanov, D. V. & Ignatova, G. A. 2002 Comparison of calculated and experimental data on supersonic flow past a circular cylinder. Fluid Dyn. 37 (3), 473–483.Google Scholar
Estorf, M., Wolf, T. & Radespiel, R.2003 Experimental and numerical investigations on the operation of the Hypersonic Ludwieg tube Braunschweig. Tech. Rep. Technical University at Braunschweig.Google Scholar
Fage, A. & Johansen, F. C. 1927 On the flow of air behind an inclined flat plate of infinite span. Proc. R. Soc. Lond. A 116 (773), 170–197.Google Scholar
Gowen, F. E. & Perkins, E. W.1953 Drag of circular cylinders for a wide range of Reynolds numbers and Mach numbers. Tech. Rep. Technical Note 2960. National Advisory Committee for Aeronautics.Google Scholar
Kim, C.-S. 1956 Experimental studies of supersonic flow past a circular cylinder. J. Phys. Soc. Japan 11 (4), 439–445.Google Scholar
Parziale, N. J., Damazo, J. S., Schmidt, B. E., Wang, P. S., Hornung, H. G. & Shepherd, J. E. 2015 Pulsed laser diode for use as a light source for short-exposure, high-frame-rate flow visualization. In AIAA SciTech 2015, AIAA.Google Scholar
Quirk, J. J. 1998 AMRITA: a computational facility (for CFD modelling). Lecture Series – von Karman Institute for Fluid Dyn. 3, D1–D72.Google Scholar
Relf, E. F. & Simmons, L. F. G. 1924 The frequency of eddies generated by the motion of circular cylinders through a fluid. Aero. Res. Couc., Lond., Rep. and Mem. no. 917.Google Scholar
Roshko, A.1953 On the development of turbulent wakes from vortex streets. NACA Tech. Rep. TN 2913. National Advisory Committee for Aeronautics.Google Scholar
Roshko, A.1954 On the drag and shedding frequency of two-dimensional bluff bodies. Tech. Rep. 3169. National Advisory Committee for Aeronautics.Google Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10 (3), 345–356.Google Scholar
Sandberg, R. D. 2012 Numerical investigation of turbulent supersonic axisymmetric wakes. J. Fluid Mech. 702, 488–520.CrossRefGoogle Scholar
Sandberg, R. D. & Fasel, H. F. 2006 Numerical investigation of transitional supersonic axisymmetric wakes. J. Fluid Mech. 563, 1–41.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar

Schmidt supplementary movie

Pseudo-schlieren movie of the Euler computation performed in AMRITA. The cylinder is shown in blue and sonic lines are shown in white.

Download Schmidt supplementary movie(Video)
Video 27 MB

Schmidt supplementary movie

Pseudo-schlieren movie of the Euler computation performed in AMRITA. The cylinder is shown in blue and sonic lines are shown in white.

Download Schmidt supplementary movie(Video)
Video 18.8 MB

Schmidt supplementary movie

Short excerpt of a shadowgraph movie from the experiments. Images were recorded at 200 000 frames per second and are played back at 30 frames per second.

Download Schmidt supplementary movie(Video)
Video 35.5 MB

Schmidt supplementary movie

Short excerpt of a shadowgraph movie from the experiments. Images were recorded at 200 000 frames per second and are played back at 30 frames per second.

Download Schmidt supplementary movie(Video)
Video 49.1 MB