Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T03:42:44.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Passive scalar decay laws in isotropic turbulence: Prandtl number effects

Published online by Cambridge University Press:  04 November 2015

A. Briard ,
T. Gomez ,
P. Sagaut  and
S. Memari
A. Briard
Affiliation:
Insitut Jean Le Rond d’Alembert, CNRS UMR 7190, F-75252 Paris CEDEX 5, France
T. Gomez*
Affiliation:
Insitut Jean Le Rond d’Alembert, CNRS UMR 7190, F-75252 Paris CEDEX 5, France Université Lille Nord de France, F-59000 Lille, France USTL, LML, F-59650 Villeneuve d’Ascq, France
P. Sagaut
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, M2P2 UMR 7340, 13451 Marseille, France
S. Memari
Affiliation:
Insitut Jean Le Rond d’Alembert, CNRS UMR 7190, F-75252 Paris CEDEX 5, France
*
†Email address for correspondence: thomas.gomez@univ-lille1.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The passive scalar dynamics in a freely decaying turbulent flow is studied. The classical framework of homogeneous isotropic turbulence without forcing is considered. Both low and high Reynolds number regimes are investigated for very small and very large Prandtl numbers. The long time behaviours of integrated quantities such as the scalar variance or the scalar dissipation rate are analysed by considering that the decay follows power laws. This study addresses three major topics. First, the Comte-Bellot and Corrsin (CBC) dimensional analysis for the temporal decay exponents is extended to the case of a passive scalar when the permanence of large eddies is broken. Secondly, using numerical simulations based on an eddy-damped quasi-normal Markovian (EDQNM) model, the time evolution of integrated quantities is accurately determined for a wide range of Reynolds and Prandtl numbers. These simulations show that, whatever the values of the Reynolds and the Prandtl numbers are, the decay follows an algebraic law with an exponent very close to the value predicted by the CBC theory. Finally, the initial position of the scalar integral scale 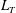$L_{T}$ has no influence on the asymptotic values of the decay exponents, and an analytical law predicting the relative positions of the kinetic and scalar spectra peaks is derived.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 274 - 303
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Lee, S. K., Djenidi, L. & Danaila, L. 2013 Invariants for slightly heated decaying grid turbulence. J. Fluid Mech. 727, 379–406.CrossRefGoogle Scholar
Antonia, R. A. & Orlandi, P. 2004 Similarity of decaying isotropic turbulence with a passive scalar. J. Fluid Mech. 505, 123–151.CrossRefGoogle Scholar
Batchelor, G. K., Howells, I. D. & Townsend, A. A. 1958 Small-scale variation of convected quantities like temperature in turbulent fluid. J. Fluid Mech. 5.Google Scholar
Batchelor, G. K. & Proudman, I. 1956 The large-scale structure of homogeneous turbulence. Phil. Trans. R. Soc. Lond. A 248, 369–405.Google Scholar
Briard, A. & Gomez, T. 2015 A passive scalar convective-diffusive subrange for low prandtl numbers in isotropic turbulence. Phys. Rev. E 91 (1), 011001.Google ScholarPubMed
Chasnov, J., Canuto, V. M. & Rogallo, R. S. 1988 Turbulence spectrum of a passive temperature field: results of a numerical simulation. Phys. Fluids 31, 2065–2067.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of a grid generated turbulence. J. Fluid Mech. 25, 657–682.CrossRefGoogle Scholar
Corrsin, S. 1951 The decay of isotropic temperature fluctuations in an isotropic turbulence. J. Aero. Sci. 18, 417.Google Scholar
Danaila, L., Zhou, T., Anselmet, F. & Antonia, R. A. 2000 Calibration of a temperature dissipation probe in decaying grid turbulence. Exp. Fluids 28, 45–50.CrossRefGoogle Scholar
Eyink, G. L. & Thomson, D. J. 2000 Free decay of turbulence and breakdown of self-similarity. Phys. Fluids 12, 477–479.CrossRefGoogle Scholar
Goto, S. & Kida, S. 1999 Passive scalarspectrum in isentropic turbulence: prediction by the lagrangian direct-interaction approximation. Phys. Fluids 11.CrossRefGoogle Scholar
Granatstein, V. L. & Buchsbaum, S. J. 1966 Fluctuation spectrum of a plasma additive in a turbulence gas. Phys. Rev. Lett. 16, 504–507.CrossRefGoogle Scholar
Grant, H. L., Hughes, B. A., Vogel, W. M. & Moilliet, A. 1968 The spectrum of temperature fluctuations in turbulent flow. J. Fluid Mech. 34, 423–442.CrossRefGoogle Scholar
Herring, J. R. & Kerr, R. M. 1982 Comparison of direct numerical simulations with predictions of two-point closures for isotropic turbulence convecting a passive scalar. J. Fluid Mech. 118, 205–219.CrossRefGoogle Scholar
Herring, J. R., Schertzer, D., Lesieur, M., Newman, G. R., Chollet, J. P. & Larcheveque, M. 1982 A comparative assessment of spectral closures as applied to passive scalar diffusion. J. Fluid Mech. 124, 411–437.CrossRefGoogle Scholar
Kaneda, Y. 1986 Inertial range structure of turbulent velocity and scalar fields in a lagrangian renormalized approximation. Phys. Fluids 29.CrossRefGoogle Scholar
Kraichnan, R. H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11 (5), 945–953.CrossRefGoogle Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.CrossRefGoogle Scholar
Lee, S. K. & Antonia, R. A. 2012 Scaling range of velocity and passive scalar spectra in grid turbulence. Phys. Fluids 24.Google Scholar
Leith, C. E. 1971 Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 28, 145.2.0.CO;2>CrossRefGoogle Scholar
Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Martinus Nijhoff.CrossRefGoogle Scholar
Lesieur, M., Montmory, C. & Chollet, J. P. 1987 The decay of kinetic energy and temperature variance in threedimensional isotropic turbulence. Phys. Fluids 30.CrossRefGoogle Scholar
Lesieur, M. & Ossia, S. 2000 3D isotropic turbulence at very high Reynolds numbers: EDQNM study. J. Fluid Mech. 1 (17).Google Scholar
Lesieur, M. & Rogallo, R. 1989 Large-eddy simulation of passive-scalar diffusion in isotropic turbulence. Phys. Fluids A 1, 718–722.CrossRefGoogle Scholar
Lesieur, M. & Schertzer, D. 1978 Amortissement auto similaire d’une turbulence à grand nombre de Reynolds. J. Mec. 17.Google Scholar
Lin, S. C. & Lin, S. C. 1973 Turbulence spectrum of a passive temperature field: results of a numerical simulation. Phys. Fluids 16, 1587–1598.CrossRefGoogle Scholar
Llor, A. & Soulard, O. 2013 Comment on energy spectra at low wavenumbers in homogeneous incompressible turbulence. Phys. Lett. A 377, 1157–1159; (Phys. Lett. A 375 (2011) 2850).CrossRefGoogle Scholar
Lumley, J. L. 1970 Stochastic Tools in Turbulence. Academic.Google Scholar
Marinis, D., Chibbaro, S., Meldi, M. & Sagaut, P. 2013 Temperature dynamics in decaying isotropic turbulence with joule heat production. J. Fluid Mech. 724.CrossRefGoogle Scholar
Meldi, M. & Sagaut, P. 2012 On non-self-similar regimes in homogeneous isotropic turbulence decay. J. Fluid Mech. 711, 364–393.CrossRefGoogle Scholar
Meldi, M. & Sagaut, P. 2013 Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.CrossRefGoogle Scholar
Meyers, J. & Meneveau, C. 2008 A functional form of the energy spectrum parametrizing bottleneck and intermittency effects. Phys. Fluids 20.CrossRefGoogle Scholar
Mons, V., Chassaing, J. C., Gomez, T. & Sagaut, P. 2014 Is isotropic turbulence decay governed by asymptotic behavior of large scales? An eddy-damped quasi-normal Markovian-based data assimilation study. Phys. Fluids 26.CrossRefGoogle Scholar
Nelkin, M. & Kerr, R. M. 1981 Decay of scalar variance in terms of a modified Richardson law of pair dispersion. Phys. Fluids 24, 1754.CrossRefGoogle Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.CrossRefGoogle Scholar
Orszag, S. A. 1977 The statistical theory of turbulence. In Fluid Dynamics (ed. Balian, A. & Peube, J. L.), pp. 237–374. Gordon and Breach.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pouquet, A., Lesieur, M., Andre, J. C. & Basdevant, C. 1975 Evolution of high Reynolds number two-dimensional turbulence. J. Fluid Mech. 77.Google Scholar
Ristorcelli, J. R. 2006 Passive scalar mixing: analytic study of time scale ratio, variance, and mix rate. Phys. Fluids 18.CrossRefGoogle Scholar
Ristorcelli, J. R. & Livescu, D. 2004 Decay of isotropic turbulence: fixed points and solutions for $g\sim R_{{\it\lambda}}$ palinstrophy. Phys. Fluids 16, 3487.CrossRefGoogle Scholar
Rust, J. H. & Sesonske, A. 1966 Turbulent temperature fluctuations in mercury and ethylene glycol in pipe flow. Intl J. Heat Mass Transfer 9, 215–227.CrossRefGoogle Scholar
Saffman, P. G. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 551–593.CrossRefGoogle Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Sirivat, A. & Warhaft, Z. 1983 The effect of a passive cross-stream temperature gradient on the evolution of temperature variance and heat flux in grid turbulence. J. Fluid Mech. 128, 323–346.CrossRefGoogle Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the Obukhov–Corrsin constant. Phys. Fluids 8 (1), 189–196.CrossRefGoogle Scholar
Sreenivasan, K. R., Tavoularis, S., Henry, R. & Corrsin, S. 1980 Temperature fluctuations and scales in grid generated turbulence. J. Fluid Mech. 100, 597–621.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.CrossRefGoogle Scholar
Warhaft, Z. & Lumley, J. L. 1978 An experimental study of the decay of temperature fluctuations in grid generated turbulence. J. Fluid Mech. 88, 659–684.CrossRefGoogle Scholar
Yeung, P. K., Xu, S. & Sreenivasan, K. R. 2002 Schmidt number effects on turbulent transport with uniform mean scalar gradient. Physics of Fluids 14 (12), 4178–4191.CrossRefGoogle Scholar
Yeung, P. K., Xu, S., Donzis, D. A. & Sreenivasan, K. R. 2004 Simulations of three-dimensional turbulent mixing for Schmidt numbers of the order 1000. Flow Turbul. Combust. 72, 333–347.CrossRefGoogle Scholar
Zhou, T., Antonia, R. A. & Chua, L. P. 2002 Performance of a probe for measuring turbulent energy and temperature dissipation rates. Exp. Fluids 33, 334–345.CrossRefGoogle Scholar
Zhou, T., Antonia, R. A., Danaila, L. & Anselmet, F. 2000 Transport equations for the mean energy and temperature dissipation rates grid turbulence. Exp. Fluids 28, 143–151.CrossRefGoogle Scholar