Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T18:02:55.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Propagation of a viscous thin film over an elastic membrane

Published online by Cambridge University Press:  06 November 2015

Zhong Zheng ,
Ian M. Griffiths  and
Howard A. Stone
Zhong Zheng*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Ian M. Griffiths
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK
Howard A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: zzheng@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the buoyancy-driven spreading of a thin viscous film over a thin elastic membrane. Neglecting the effects of membrane bending and the membrane weight, we study the case of constant fluid injection and obtain a system of coupled partial differential equations to describe the shape of the air–liquid interface, and the deformation and radial tension of the stretched membrane. We obtain self-similar solutions to describe the dynamics. In particular, in the early-time period, the dynamics is dominated by buoyancy-driven spreading of the liquid film, and membrane stretching is a response to the buoyancy-controlled distribution of liquid weight; the location of the liquid front obeys the power-law form 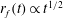$r_{f}(t)\propto t^{1/2}$. However, in the late-time period, the system is quasi-steady, the air–liquid interface is flat, and membrane stretching, due to the liquid weight, causes the spreading of the liquid front; the location of the front obeys a different power-law form 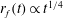$r_{f}(t)\propto t^{1/4}$ before the edge effects of the membrane become significant. In addition, we report laboratory experiments for constant fluid injection using different viscous liquids and thin elastic membranes. Very good agreement is obtained between the theoretical predictions and experimental observations.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 443 - 464
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J., Cawthorn, C. J. & Craster, R. V. 2010 Contact in a viscous fluid. Part 2. A compressible fluid and an elastic solid. J. Fluid Mech. 646, 339–361.Google Scholar
Barenblatt, G. I. 1979 Similarity, Self-Similarity, and Intermediate Asymptotics. Consultants Bureau.CrossRefGoogle Scholar
Bico, J., Roman, B., Moulin, L. & Boudaoud, A. 2004 Adhesion: elastocapillary coalescence in wet hair. Nature 432, 690.Google Scholar
Boys, C. V. 1959 Soap Bubbles, Their Colours and the Forces Which Mold Them. Courier Corporation.Google Scholar
Bunger, A. P. & Cruden, A. R. 2011 Modeling the growth of laccoliths and large mafic sills: role of magma body forces. J. Geophys. Res. 116, B2.Google Scholar
Chopin, J., Vella, D. & Boudaoud, A. 2008 The liquid blister test. Proc. R. Soc. Lond. A 464, 2887–2906.Google Scholar
Didden, N. & Maxworthy, T. 1982 The viscous spreading of plane and axisymmetric gravity currents. J. Fluid Mech. 121, 27–42.Google Scholar
Duprat, C., Protiere, S., Beebe, A. Y. & Stone, H. A. 2012 Wetting of flexible fibre arrays. Nature 482, 510–513.Google Scholar
Gohar, R. 2001 Elastohydrodynamics. World Scientific.Google Scholar
Grotberg, J. B. 2011 Respiratory fluid mechanics. Phys. Fluids 23, 021301.CrossRefGoogle ScholarPubMed
Halpern, D. & Grotberg, J. B. 1992 Fluid–elastic instabilities of liquid-lined flexible tubes. J. Fluid Mech. 244, 615–632.CrossRefGoogle Scholar
Halpern, D. & Grotberg, J. B. 1993 Surfactant effects on fluid–elastic instabilities of liquid-lined flexible tubes: a model of airway closure. Trans. ASME J. Biomech. Engng 115, 271–277.Google Scholar
Hewitt, I. J., Balmforth, N. J. & De Bruyn, J. R. 2015 Elastic-plated gravity currents. Eur. J. Appl. Maths 26, 1–31.CrossRefGoogle Scholar
Howell, P. D., Robinson, J. & Stone, H. A. 2013 Gravity-driven thin-film flow on a flexible substrate. J. Fluid Mech. 732, 190–213.CrossRefGoogle Scholar
Huang, J., Juszkiewicz, M., de Jeu, W. H., Cerda, E., Emrick, T., Menon, N. & Russell, T. P. 2007 Capillary wrinkling of floating thin polymer films. Science 317, 650–653.Google Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.Google Scholar
Jensen, H. M. 1991 The blister test for interface toughness measurement. Eng. Fract. Mech. 40, 475–486.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Theory of Elasticity. Pergamon.Google Scholar
Lister, J. R., Peng, G. G. & Neufeld, J. A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111, 154501.Google Scholar
Macklem, P. T., Proctor, D. F. & Hogg, J. C. 1970 The stability of peripheral airways. Respir. Physiol. 8, 191–203.Google Scholar
Mastrangelo, C. H. & Hsu, C. H. 1993a Mechanical stability and adhesion of microstructures under capillary forces. I. Basic theory. J. Microelectromech. Syst. 2, 33–43.Google Scholar
Mastrangelo, C. H. & Hsu, C. H. 1993b Mechanical stability and adhesion of microstructures under capillary forces. II. Experiments. J. Microelectromech. Syst. 2, 44–55.Google Scholar
Matar, O. K., Craster, R. V. & Kumar, S. 2007 Falling films on flexible inclines. Phys. Rev. E 76, 056301.Google Scholar
Matar, O. K. & Kumar, S. 2004 Rupture of a surfactant-covered thin liquid film on a flexible wall. SIAM J. Appl. Maths 64, 2144–2166.Google Scholar
Matar, O. K. & Kumar, S. 2007 Dynamics and stability of flow down a flexible incline. J. Engng Maths 57, 145–158.CrossRefGoogle Scholar
Michaut, C. 2011 Dynamics of magmatic intrusions in the upper crust: Theory and applications to laccoliths on Earth and the Moon. J. Geophys. Res. 116, B5.Google Scholar
Pihler-Puzović, D., Illien, P., Heil, M. & Juel, A. 2012 Suppression of complex fingerlike patterns at the interface between air and a viscous fluid by elastic membranes. Phys. Rev. Lett. 108, 074502.Google Scholar
Pihler-Puzović, D., Périllat, R., Russell, M., Juel, A. & Heil, M. 2013 Modelling the suppression of viscous fingering in elastic-walled Hele-Shaw cells. J. Fluid Mech. 731, 162–183.Google Scholar
Rogers, J. A, Someya, T. & Huang, Y. 2010 Materials and mechanics for stretchable electronics. Science 327, 1603–1607.Google Scholar
Smith, S. H. 1969 On initial value problems for the flow in a thin sheet of viscous liquid. Z. Angew. Math. Phys. 20, 556–560.Google Scholar
Tanaka, T., Morigami, M. & Atoda, N. 1993 Mechanism of resist pattern collapse during development process. Japan. J. Appl. Phys. 32, 6059–6064.Google Scholar
Unger, M. A., Chou, H., Thorsen, T., Scherer, A. & Quake, S. R. 2000 Monolithic microfabricated valves and pumps by multilayer soft lithography. Science 288, 113–116.Google Scholar
Vella, D., Adda-Bedia, M. & Cerda, E. 2010 Capillary wrinkling of elastic membranes. Soft Matt. 6, 5778–5782.Google Scholar
Yin, X. & Kumar, S. 2005 Lubrication flow between a cavity and a flexible wall. Phys. Fluids 17, 063101.Google Scholar
Yin, X. & Kumar, S. 2006 Two-dimensional simulations of flow near a cavity and a flexible solid boundary. Phys. Fluids 18, 063103.Google Scholar
Zheng, Z., Rongy, L. & Stone, H. A. 2015 Viscous fluid injection into a confined channel. Phys. Fluids 27, 062105.Google Scholar