Article contents
Quantification of turbulent mixing in colliding gravity currents
Published online by Cambridge University Press: 19 July 2018
Abstract
Collision between two identical counterflowing gravity currents was studied in the laboratory with the goal of understanding the fundamental turbulent mixing physics of flow collisions in nature, for example katabatic flows and thunderstorm outflows. The ensuing turbulent mixing is a subgrid process in mesoscale forecasting models, and needs to be parameterized using eddy diffusivity. Laboratory gravity currents were generated by simultaneously removing two identical locks, located at both ends of a long rectangular tank, which separated dense and lighter water columns with free surfaces of the same depth 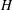 $H$. The frontal velocity
$H$. The frontal velocity 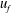 $u_{f}$ and the velocity and density fields of the gravity currents were monitored using time-resolved particle image velocimetry and planar laser-induced fluorescence imaging. Ensemble averaging of identical experimental realizations was used to compute turbulence statistics, after removing inherent jitter via phase alignment of successive data realizations by iteratively maximizing the cross-correlation of each realization with the ensemble average. Four stages of flow evolution were identified: initial (independent) propagation of gravity currents, their approach while influencing one another, collision and resulting updraughts, and postcollision slumping of collided fluid. The collision stage, in turn, involved three phases, and produced the strongest turbulent mixing as quantified by the rate of change of density. Phase I spanned
$u_{f}$ and the velocity and density fields of the gravity currents were monitored using time-resolved particle image velocimetry and planar laser-induced fluorescence imaging. Ensemble averaging of identical experimental realizations was used to compute turbulence statistics, after removing inherent jitter via phase alignment of successive data realizations by iteratively maximizing the cross-correlation of each realization with the ensemble average. Four stages of flow evolution were identified: initial (independent) propagation of gravity currents, their approach while influencing one another, collision and resulting updraughts, and postcollision slumping of collided fluid. The collision stage, in turn, involved three phases, and produced the strongest turbulent mixing as quantified by the rate of change of density. Phase I spanned 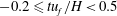 $-0.2\leqslant tu_{f}/H<0.5$, where collision produced a rising density front (interface) with strong shear and intense turbulent kinetic energy production (
$-0.2\leqslant tu_{f}/H<0.5$, where collision produced a rising density front (interface) with strong shear and intense turbulent kinetic energy production ( $t$ is a suitably defined time coordinate such that gravity currents make the initial contact at
$t$ is a suitably defined time coordinate such that gravity currents make the initial contact at 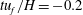 $tu_{f}/H=-0.2$). In Phase II (
$tu_{f}/H=-0.2$). In Phase II (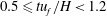 $0.5\leqslant tu_{f}/H<1.2$), the interface was flat and calm with negligible vertical velocity. Phase III (
$0.5\leqslant tu_{f}/H<1.2$), the interface was flat and calm with negligible vertical velocity. Phase III (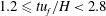 $1.2\leqslant tu_{f}/H<2.8$) was characterized by slumping which led to hydraulic bores propagating away from the collision area. The measurements included root mean square turbulent velocities and their decay rates, interfacial velocity, rate of change of fluid-parcel density, and eddy diffusivity. These measures depended on the Reynolds number
$1.2\leqslant tu_{f}/H<2.8$) was characterized by slumping which led to hydraulic bores propagating away from the collision area. The measurements included root mean square turbulent velocities and their decay rates, interfacial velocity, rate of change of fluid-parcel density, and eddy diffusivity. These measures depended on the Reynolds number 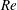 $Re$, but appeared to achieve Reynolds number similarity for
$Re$, but appeared to achieve Reynolds number similarity for 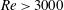 $Re>3000$. The eddy diffusivity
$Re>3000$. The eddy diffusivity 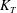 $K_{T}$, space–time averaged over the spatial extent (
$K_{T}$, space–time averaged over the spatial extent (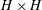 $H\times H$) and the lifetime (
$H\times H$) and the lifetime (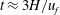 $t\approx 3H/u_{f}$) of collision, was
$t\approx 3H/u_{f}$) of collision, was 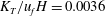 $K_{T}/u_{f}H=0.0036$ for
$K_{T}/u_{f}H=0.0036$ for 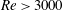 $Re>3000$, with the area
$Re>3000$, with the area  $A$ of active mixing being
$A$ of active mixing being 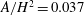 $A/H^{2}=0.037$.
$A/H^{2}=0.037$.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 20
- Cited by



