Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T07:33:28.260Z Has data issue: false hasContentIssue false
  • English
  • Français

Revisiting inclination of large-scale motions in unstably stratified channel flow

Published online by Cambridge University Press:  17 December 2019

Scott T. Salesky Open the ORCID record for Scott T. Salesky [Opens in a new window]  and
W. Anderson Open the ORCID record for W. Anderson [Opens in a new window]
Scott T. Salesky*
Affiliation:
School of Meteorology, The University of Oklahoma, Norman, OK73072, USA
W. Anderson
Affiliation:
Mechanical Engineering Department, The University of Texas at Dallas, Richardson, TX75080, USA
*
†Email address for correspondence: salesky@ou.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

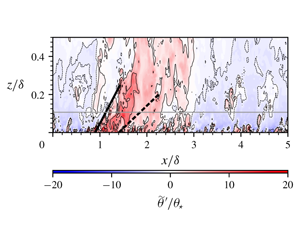
Observational and computational studies of inertia-dominated wall turbulence with unstable thermal stratification have demonstrated that the inclination angle of large-scale motions (LSMs) increases with increasing buoyancy (as characterized by the Monin–Obukhov stability variable $\unicode[STIX]{x1D701}_{z}$). The physical implications of this structural steepening have received relatively less attention. Some authors have proposed that LSMs thicken – yet remain attached to the wall – with increasing buoyancy (Salesky & Anderson, J. Fluid Mech., vol. 856, 2018, pp. 135–168), while others have presented evidence that the upstream edge of an LSM remains anchored to the wall while its downstream edge lifts away from the wall (Hommema & Adrian, Boundary-Layer Meteorol., vol. 106, 2003, pp. 147–170). Using a suite of large-eddy simulations (LES) of unstably stratified turbulent channel flow, we demonstrate that buoyancy acts to lift LSMs away from the wall, leaving a wedge of fluid beneath with differing momentum. We develop a prognostic model for LSM inclination angle that accounts for this observed structure, where the LSM inclination angle $\unicode[STIX]{x1D6FE}$ is the sum of the inclination angle observed in a neutrally stratified wall-bounded turbulent flow, $\unicode[STIX]{x1D6FE}_{0}\approx 12^{\circ }{-}15^{\circ }$, and the stability-dependent inclination angle of the wedge $\unicode[STIX]{x1D6FE}_{w}(\unicode[STIX]{x1D701}_{z})$. Reported values of $\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D701}_{z})$ from the literature, LES results and atmospheric surface layer observations are found to be in good agreement with the new model for $\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D701}_{z})$.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , R5
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. 1981 Conditional sampling in turbulence measurement. Annu. Rev. Fluid Mech. 13, 131–156.CrossRefGoogle Scholar
Carper, M. A. & Porté-Agel, F. 2004 The role of coherent structures in subfilter-scale dissipation of turbulence measured in the atmospheric surface layer. J. Turbul. 5, 32–32.Google Scholar
Chauhan, K., Hutchins, N., Monty, J. & Marusic, I. 2013 Structure inclination angles in the convective atmospheric surface layer. Boundary-Layer Meteorol. 147 (1), 41–50.CrossRefGoogle Scholar
Deshpande, R., Monty, J. P. & Marusic, I. 2019 Streamwise inclination angle of large wall-attached structures in turbulent boundary layers. J. Fluid Mech. 877, R4.CrossRefGoogle Scholar
Fan, D., Xu, J., Yao, M. X. & Hickey, J.-P. 2019 On the detection of internal interfacial layers in turbulent flows. J. Fluid Mech. 872, 198–217.CrossRefGoogle Scholar
Hommema, S. E. & Adrian, R. J. 2003 Packet structure of surface eddies in the atmospheric boundary layer. Boundary-Layer Meteorol. 106 (1), 147–170.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Marusic, I. & Heuer, W. D. C. 2007 Reynolds number invariance of the structure inclination angle in wall turbulence. Phys. Rev. Lett. 99 (11), 114504.CrossRefGoogle ScholarPubMed
Salesky, S. T. & Anderson, W. 2018 Buoyancy effects on large-scale motions in convective atmospheric boundary layers: implications for modulation of near-wall processes. J. Fluid Mech. 856, 135–168.CrossRefGoogle Scholar
Salesky, S. T. & Chamecki, M. 2012 Random errors in turbulence measurements in the atmospheric surface layer: implications for Monin–Obukhov similarity theory. J. Atmos. Sci. 69 (12), 3700–3714.CrossRefGoogle Scholar
Salesky, S. T., Chamecki, M. & Bou-Zeid, E. 2017 On the nature of the transition between roll and cellular organization in the convective boundary layer. Boundary-Layer Meteorol. 163 (1), 41–68.CrossRefGoogle Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.CrossRefGoogle Scholar