Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Podvin, Bérengère
Pellerin, Stéphanie
Fraigneau, Yann
Evrard, Antoine
and
Cadot, Olivier
2020.
Proper orthogonal decomposition analysis and modelling of the wake deviation behind a squareback Ahmed body.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Urquhart, Magnus
Varney, Max
Sebben, Simone
and
Passmore, Martin
2020.
Aerodynamic drag improvements on a square-back vehicle at yaw using a tapered cavity and asymmetric flaps.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108737.
Haffner, Y.
Borée, J.
Spohn, A.
and
Castelain, T.
2020.
Mechanics of bluff body drag reduction during transient near-wake reversals.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Szodrai, Ferenc
2020.
Quantitative Analysis of Drag Reduction Methods for Blunt Shaped Automobiles.
Applied Sciences,
Vol. 10,
Issue. 12,
p.
4313.
Fan, Yajun
Xia, Chao
Chu, Shijun
Yang, Zhigang
and
Cadot, Olivier
2020.
Experimental and numerical analysis of the bi-stable turbulent wake of a rectangular flat-backed bluff body.
Physics of Fluids,
Vol. 32,
Issue. 10,
Lorite-Díez, M.
Jiménez-González, J. I.
Pastur, L.
Cadot, O.
and
Martínez-Bazán, C.
2020.
Drag reduction of three-dimensional bodies by base blowing with various gas densities.
Physical Review E,
Vol. 102,
Issue. 1,
Aultman, Matthew
Auza-Gutierrez, Rodrigo
Disotell, Kevin
and
Duan, Lian
2021.
Effects of Wheel Rotation on Long-Period Wake Dynamics of the DrivAer Fastback Model.
Fluids,
Vol. 7,
Issue. 1,
p.
19.
He, Kan
Minelli, Guglielmo
Wang, Jiabin
Dong, Tianyun
Gao, Guangjun
and
Krajnović, Siniša
2021.
Numerical investigation of the wake bi-stability behind a notchback Ahmed body.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
He, Kan
Minelli, Guglielmo
Su, Xinchao
Gao, Guangjun
and
Krajnović, Siniša
2021.
Influence of the rounded rear edge on wake bi-stability of a notchback bluff body.
Physics of Fluids,
Vol. 33,
Issue. 11,
Podvin, Bérengère
Pellerin, Stéphanie
Fraigneau, Yann
Bonnavion, Guillaume
and
Cadot, Olivier
2021.
Low-order modelling of the wake dynamics of an Ahmed body.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Butcher, Daniel
and
Spencer, Adrian
2021.
Analysis of Multi-Stream Fuel Injector Flow Using Zonal Proper Orthogonal Decomposition.
Energies,
Vol. 14,
Issue. 6,
p.
1789.
Yu, Zhou
and
Bingfu, Zhang
2021.
Recent Advances in Wake Dynamics and Active Drag Reduction of Simple Automotive Bodies.
Applied Mechanics Reviews,
Vol. 73,
Issue. 6,
Aleyasin, Seyed Sobhan
Tachie, Mark Francis
and
Balachandar, Ram
2021.
Characteristics of flow past elongated bluff bodies with underbody gaps due to varying inflow turbulence.
Physics of Fluids,
Vol. 33,
Issue. 12,
Urquhart, Magnus
Varney, Max
Sebben, Simone
and
Passmore, Martin
2021.
Drag reduction mechanisms on a generic square-back vehicle using an optimised yaw-insensitive base cavity.
Experiments in Fluids,
Vol. 62,
Issue. 12,
He, Kan
Minelli, Guglielmo
Su, Xinchao
Gao, Guangjun
and
Krajnović, Siniša
2021.
Blockage influence on bi-stable flows of a notchback bluff body.
Physics of Fluids,
Vol. 33,
Issue. 12,
Kang, Nam
Essel, Ebenezer E.
Roussinova, Vesselina
and
Balachandar, Ram
2021.
Effects of approach flow conditions on the unsteady three-dimensional wake structure of a square-back Ahmed body.
Physical Review Fluids,
Vol. 6,
Issue. 3,
Fan, Yajun
Parezanović, Vladimir
and
Cadot, Olivier
2022.
Wake transitions and steady -instability of an Ahmed body in varying flow conditions.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
He, Kan
Minelli, Guglielmo
Su, Xinchao
Wang, Jiabin
Gao, Guangjun
and
Krajnović, Siniša
2022.
Floor motion's influence on wake asymmetry of a notchback bluff body.
Physics of Fluids,
Vol. 34,
Issue. 3,
de Boer, Marc
Gaylard, Adrian P.
and
Parmar, Bhavik
2022.
The Aerodynamic Development of the New Range Rover Evoque.
SAE International Journal of Advances and Current Practices in Mobility,
Vol. 5,
Issue. 1,
p.
97.
Booysen, Adriaan
Das, Prashant
and
Ghaemi, Sina
2022.
Large-scale 3D-PTV measurement of Ahmed-body wake in crossflow.
Experimental Thermal and Fluid Science,
Vol. 132,
Issue. ,
p.
110562.
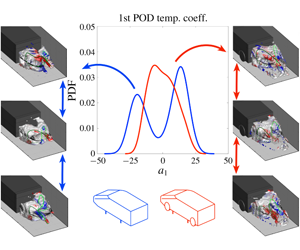
 $Re_{H}=5.78\times 10^{5}$ (based on the model height). In the no-wheel case, the time-averaged wake features a balanced toroidal shape, with a good level of symmetry in both vertical and lateral directions. However, analysis of the wake dynamics shows this widely accepted result to be a poor model of the wake structure. Application of proper orthogonal decomposition to the unsteady data reveals the existence of the widely reported bi-stable behaviour, consisting of random switches between two lateral symmetry-breaking states. For the first time, the three-dimensional topology of each state is fully characterised and the changes in wake topology during the switches between bi-stable states are also described. Each symmetry-breaking state is shown to feature a characteristic ‘hairpin vortex’ structure that is the result of the merging of two horseshoe vortices, aligned with the vertical edges of the model base. The mutual interactions between these vortices are found to be at the origin of the bi-stable mode. The vertical symmetry is lost when wheels are added to the model, resulting in the formation of an upwash-dominated wake. The bi-stable behaviour is removed but considerable mobility in the near wake remains, in the form of a swinging motion of the rear recirculation.
$Re_{H}=5.78\times 10^{5}$ (based on the model height). In the no-wheel case, the time-averaged wake features a balanced toroidal shape, with a good level of symmetry in both vertical and lateral directions. However, analysis of the wake dynamics shows this widely accepted result to be a poor model of the wake structure. Application of proper orthogonal decomposition to the unsteady data reveals the existence of the widely reported bi-stable behaviour, consisting of random switches between two lateral symmetry-breaking states. For the first time, the three-dimensional topology of each state is fully characterised and the changes in wake topology during the switches between bi-stable states are also described. Each symmetry-breaking state is shown to feature a characteristic ‘hairpin vortex’ structure that is the result of the merging of two horseshoe vortices, aligned with the vertical edges of the model base. The mutual interactions between these vortices are found to be at the origin of the bi-stable mode. The vertical symmetry is lost when wheels are added to the model, resulting in the formation of an upwash-dominated wake. The bi-stable behaviour is removed but considerable mobility in the near wake remains, in the form of a swinging motion of the rear recirculation.