Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-14T02:59:49.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Secondary instability analysis of crossflow on a hypersonic yawed straight circular cone

Published online by Cambridge University Press:  28 December 2016

Alexander J. Moyes ,
Pedro Paredes ,
Travis S. Kocian  and
Helen L. Reed
Alexander J. Moyes*
Affiliation:
Texas A&M University, College Station, TX 77843, USA
Pedro Paredes
Affiliation:
Universidad Politécnica de Madrid, Madrid 28040, Spain
Travis S. Kocian
Affiliation:
Texas A&M University, College Station, TX 77843, USA
Helen L. Reed
Affiliation:
Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: amoyes@tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this paper is to provide secondary instability analysis of stationary crossflow vortices on a hypersonic yawed straight circular cone with a 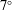$7^{\circ }$ half-angle at 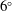$6^{\circ }$ angle of attack, free-stream Mach number 6 and unit Reynolds number 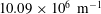$10.09\times 10^{6}~\text{m}^{-1}$. At an angle of attack, a three-dimensional boundary layer is developed between the windward and leeward symmetry planes. Under the action of azimuthal pressure gradients, the flow near the surface is deflected more than the flow near the edge of the boundary layer. This results in an inflectional velocity profile that can sustain the growth of crossflow vortices. The stationary crossflow instability is computed by means of the nonlinear parabolized stability equations, including a methodology to predict the stationary-crossflow marching path and variation of the spanwise number of waves in the marching direction solely from the basic state. Secondary instability analysis is performed using spatial BiGlobal equations based on two-dimensional partial differential equations. The secondary instabilities are calculated at different axial locations along two crossflow vortex trajectories selected to complement experiments conducted in the Mach 6 Quiet Tunnel at Texas A&M University and in the Boeing/AFOSR Mach 6 Quiet Tunnel at Purdue University. The secondary instability analysis captures various instability modes. Similar to observations in the low-speed regime for an infinite swept wing, secondary shear-layer instabilities are amplified as a consequence of the three-dimensional shear layer formed by crossflow vortices. Also, low-frequency travelling crossflow and high-frequency second modes coexist with the shear-layer instabilities. These results are shown to be in good agreement with the two sets of hypersonic yawed cone experiments (one with natural surface roughness and one with artificial discrete roughness) and compare well with experimental measurements of an incompressible swept wing.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer stability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 370 - 397
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balakumar, P. & Owens, L.2010 Stability of hypersonic boundary layers on a cone at angle of attack. AIAA Paper 2010-4718.Google Scholar
Balakumar, P. & Reed, H. 1991 Stability of three-dimensional supersonic boundary layers. Phys. Fluids 3, 617–632.Google Scholar
Bonfigli, G. & Kloker, M. 2007 Secondary instability of crossflow vortices: validation of the stability theory by direct numerical simulation. J. Fluid Mech. 583, 229–272.Google Scholar
Borg, M., Kimmel, R. & Stanfield, S. 2015 Traveling crossflow instability for the HIFiRE-5 elliptic cone. J. Spacecr. Rockets 52, 664–673.Google Scholar
Choudhari, M., Chang, C., Jentink, T., Li, F., Berger, K., Candler, G. & Kimmel, R.2009 Transition analysis for the HIFiRE-5 vehicle. AIAA Paper 2009-4056.Google Scholar
Chynoweth, B., Ward, C., Greenwood, R., Mckiernan, G., Fisher, R. & Schneider, S.2014 Measuring transition and instabilities in a Mach 6 hypersonic quiet wind tunnel. AIAA Paper 2014-2643.Google Scholar
Craig, S. & Saric, W. 2016 Crossflow instability in a hypersonic boundary layer. J. Fluid Mech. 808, 224–244.Google Scholar
Dinzl, D. & Candler, G.2015 Analysis of crossflow instability on HIFiRE-5 using direct numerical simulation. AIAA Paper 2015-0279.Google Scholar
Fischer, T. & Dallmann, U. 1991 Primary and secondary stability analysis of a three-dimensional boundary-layer flow. Phys. Fluids 3, 2378–2391.Google Scholar
Gosse, R., Kimmel, R. & Johnson, H.2010 CFD study of the HIFiRE-5 flight experiment. AIAA Paper 2010-4854.Google Scholar
Herbert, T. 1997 Parabolized stability equations. Annu. Rev. Fluid Mech. 29, 245–283.Google Scholar
Juliano, T. & Schneider, S.2010 Instability and transition on the HIFiRE-5 in a Mach-6 quiet tunnel. AIAA Paper 2010-5004.Google Scholar
Koch, W. 1992 On a degeneracy of temporal secondary instability modes in Blasius boundary-layer flow. J. Fluid Mech. 243, 319–351.Google Scholar
Kuehl, J., Perez, E. & Reed, H.2012 JoKHeR: NPSE simulations of hypersonic crossflow instability. AIAA Paper 2012-0921.Google Scholar
Lekoudis, S. 1980 Stability of the boundary layer on a swept wing with wall cooling. AIAA J. 18, 1029–1035.Google Scholar
Li, F. & Choudhari, M. 2011 Spatially developing secondary instabilities in compressible swept airfoil boundary layers. Theor. Comput. Fluid Dyn. 25, 65–84.Google Scholar
Mack, L. 1980 On the stabilization of three-dimensional boundary layers by suction and cooling. In Laminar–Turbulent Transition, pp. 223–238. Springer.Google Scholar
Mack, L.1984 Boundary layer stability theory: an AGARD special course on stability and transition of laminar flow. AGARD Report 709. pp. 3.1–3.81.Google Scholar
Malik, M., Li, F. & Chang, C. 1994 Crossflow disturbances in three-dimensional boundary layers: nonlinear development, wave interaction, and secondary instability. J. Fluid Mech. 268, 1–36.Google Scholar
Malik, M., Li, F. & Chang, C. 1996 Nonlinear crossflow disturbances and secondary instabilities in swept-wing boundary layer. In IUTAM Symposium on Nonlinear Instability and Transition in Three-Dimensional Boundary Layers, pp. 257–266. Springer.Google Scholar
Malik, M., Li, F., Choudhari, M. & Chang, C. 1999 Secondary instability of crossflow vortices and swept-wing boundary-layer transition. J. Fluid Mech. 399, 85–115.Google Scholar
Meier, G. & Schnerr, G. 1996 Control of flow instabilities and unsteady flows. In CISM Courses and Lectures No. 369, International Centre for Mechanical Sciences, p. 137. Springer.Google Scholar
Munoz, F., Heitmann, D. & Radespiel, R. 2014 Instability modes in boundary layers of an inclined cone at Mach 6. J. Spacecr. Rockets 51, 442–454.Google Scholar
Oliviero, N., Kocian, T., Moyes, A. & Reed, H.2015 EPIC: NPSE analysis of hypersonic crossflow instability on yawed straight circular cone. AIAA Paper 2015-2772.Google Scholar
Paredes, P.2014 Advances in global instability computations: from incompressible to hypersonic flow. PhD dissertation, Universidad Politécnica de Madrid.Google Scholar
Paredes, P., Gosse, R., Theofilis, V. & Kimmel, R. 2016 Linear modal instabilities of hypersonic flow over an elliptic cone. J. Fluid Mech. 804, 442–466.CrossRefGoogle Scholar
Paredes, P., Perez, E., Reed, H. & Theofilis, V.2014 High-frequency instabilities along the windward face of a hypersonic yawed circular cone. AIAA Paper 2014-2774.Google Scholar
Paredes, P. & Theofilis, V. 2014 Centerline instabilities on the hypersonic international flight research experimentation HIFiRE-5 elliptic cone model. J. Fluids Struct. 53, 36–49.Google Scholar
Paredes, P., Theofilis, V., Rodriguez, D. & Tendero, J.2011 The PSE-3-D instability analysis methodology for flows depending strongly on two and weakly on the third spatial dimension. AIAA Paper 2011-3752.Google Scholar
Reed, H., Perez, E., Kuehl, J., Kocian, T. & Oliviero, N. 2015 Verification and validation issues in hypersonic stability and transition prediction. J. Spacecr. Rockets 52, 29–37.Google Scholar
Reed, H. & Saric, W. 1998 Stability of 3-D boundary layers. Annu. Rev. Fluid Mech. 21, 235–284.Google Scholar
Saric, W., Reed, H. & White, E. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 413–442.Google Scholar
Sweeney, C. J., Chynoweth, B. C., Edelman, J. B. & Schneider, S. P.2016 Instability and transition experiments in the Boeing/AFOSR Mach 6 Quiet Tunnel. AIAA Paper 2016-0355.Google Scholar
Sznitko, E. 1993 Linear stability theory of three-dimensional supersonic boundary layer. J. Theor. Appl. Mech. 31, 239–262.Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar
Ward, C., Henderson, R. & Schneider, S.2015 Possible secondary instability of stationary crossflow vortices on an inclined cone at Mach 6. AIAA Paper 2015-2773.Google Scholar
White, E. & Saric, W. 2005 Secondary instability of crossflow vortices. J. Fluid Mech. 525, 275–308.Google Scholar
Wright, M.2009 Data parallel line relaxation (DPLR) code user manual Acadia version 4.01.1. NASA-TM-2009-215388.Google Scholar