Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fox, Rodney O.
2019.
A kinetic-based hyperbolic two-fluid model for binary hard-sphere mixtures.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
282.
Osnes, Andreas Nygård
Vartdal, Magnus
Omang, Marianne Gjestvold
and
Reif, Bjørn Anders Pettersson
2019.
Computational analysis of shock-induced flow through stationary particle clouds.
International Journal of Multiphase Flow,
Vol. 114,
Issue. ,
p.
268.
DeMauro, Edward P.
Wagner, Justin L.
DeChant, Lawrence J.
Beresh, Steven J.
and
Turpin, Aaron M.
2019.
Improved scaling laws for the shock-induced dispersal of a dense particle curtain.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
881.
Gai, G.
Thomine, O.
Kudriakov, S.
and
Hadjadj, A.
2020.
A new formulation of a spray dispersion model for particle/droplet-laden flows subjected to shock waves.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Osnes, Andreas Nygård
Vartdal, Magnus
Omang, Marianne Gjestvold
and
Reif, Bjørn Anders Pettersson
2020.
Particle-resolved simulations of shock-induced flow through particle clouds at different Reynolds numbers.
Physical Review Fluids,
Vol. 5,
Issue. 1,
Shallcross, Gregory S.
Fox, Rodney O.
and
Capecelatro, Jesse
2020.
A volume-filtered description of compressible particle-laden flows.
International Journal of Multiphase Flow,
Vol. 122,
Issue. ,
p.
103138.
Zhang, Duan Z.
2021.
Stress from Long-Range Interactions in Particulate Systems.
Multiscale Modeling & Simulation,
Vol. 19,
Issue. 2,
p.
1066.
Loth, Eric
Tyler Daspit, John
Jeong, Michael
Nagata, Takayuki
and
Nonomura, Taku
2021.
Supersonic and Hypersonic Drag Coefficients for a Sphere.
AIAA Journal,
p.
3261.
Hassan, Kyle
Kunz, Robert
Hanson, David
and
Manahan, Michael
2021.
A Numerical Investigation Into the Heat Transfer Performance and Particle Dynamics of a Compressible, Highly Mass Loaded, High Reynolds Number, Particle Laden Flow.
Journal of Heat Transfer,
Vol. 143,
Issue. 12,
Zhang, Duan Z.
2021.
Ensemble average and nearest particle statistics in disperse multiphase flows.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Ren, Yi
Shen, Yi
Wang, Pei
and
Ding, Hang
2021.
Simulation of interaction between shocks and particle cloud using a second-order conservative sharp interface method.
Journal of Computational Physics,
Vol. 439,
Issue. ,
p.
110410.
Osnes, Andreas Nygård
and
Vartdal, Magnus
2021.
Performance of drag force models for shock-accelerated flow in dense particle suspensions.
International Journal of Multiphase Flow,
Vol. 137,
Issue. ,
p.
103563.
Mehta, Y.
Goetsch, R.J.
Vasilyev, O.V.
and
Regele, J.D.
2022.
A particle resolved simulation approach for studying shock interactions with moving, colliding solid particles.
Computers & Fluids,
Vol. 248,
Issue. ,
p.
105670.
Fontenot, Raymond L.
Talbot, Joseph
Gale, Manuel
Mehta, Ranjan S.
and
Capecelatro, Jesse
2022.
Modeling Enhancements for Eulerian-Eulerian Two-Fluid Methods in Compressible Particle-Laden Flows with Plume-Surface Interaction Applications.
Jiang, Ling-Jie
and
Li, Maojun
2022.
Particle-resolved simulations of shock-induced inviscid flow through particle-curtain at initial stage.
Computers & Fluids,
Vol. 232,
Issue. ,
p.
105196.
Behrendt, Jacob
Balachandar, S.
and
McGrath, T. P.
2022.
Shock interacting with a random array of stationary particles underwater.
Physical Review Fluids,
Vol. 7,
Issue. 2,
St. Clair, J.
McGrath, T.
and
Balachandar, S.
2022.
Fully resolved coupled solid-fluid simulations of shock interaction with a layer of deformable aluminum particles.
Shock Waves,
Vol. 32,
Issue. 2,
p.
161.
Capecelatro, Jesse
2022.
Modeling high-speed gas–particle flows relevant to spacecraft landings.
International Journal of Multiphase Flow,
Vol. 150,
Issue. ,
p.
104008.
Xu, Yong
Zhang, Pikai
Meng, Qingyang
Li, Shangpeng
and
Zhang, Huangwei
2023.
Transmission of hydrogen detonation across a curtain of dilute inert particles.
Combustion and Flame,
Vol. 254,
Issue. ,
p.
112834.
Khalloufi, Mehdi
and
Capecelatro, Jesse
2023.
Drag force of compressible flows past random arrays of spheres.
International Journal of Multiphase Flow,
Vol. 165,
Issue. ,
p.
104496.
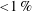 ${<}1\,\%$) the blasts that follow the shocks vary from low subsonic to supersonic, and we report data on curtain expansions and volume fraction distributions. The particle-resolving numerical simulations, run for the supersonic case, yield excellent agreement with all of these experimental data. We find that the essential feature for these good predictions is a flow choking phenomenon that entails a (particle) dispersive character of the flow down a volume fraction gradient (as at the downstream portions of the curtain). A most basic effective-field model is made to capture this gas dynamics by emulating the wake behind each particle, as seen in the particle-resolving direct Euler simulation (DES). On this basis, standard drag laws yield excellent agreement with the dispersive behaviour found in the experiment/DES, thus revealing a physics-based path to eventual well posedness of the mathematical model.
${<}1\,\%$) the blasts that follow the shocks vary from low subsonic to supersonic, and we report data on curtain expansions and volume fraction distributions. The particle-resolving numerical simulations, run for the supersonic case, yield excellent agreement with all of these experimental data. We find that the essential feature for these good predictions is a flow choking phenomenon that entails a (particle) dispersive character of the flow down a volume fraction gradient (as at the downstream portions of the curtain). A most basic effective-field model is made to capture this gas dynamics by emulating the wake behind each particle, as seen in the particle-resolving direct Euler simulation (DES). On this basis, standard drag laws yield excellent agreement with the dispersive behaviour found in the experiment/DES, thus revealing a physics-based path to eventual well posedness of the mathematical model.