Published online by Cambridge University Press: 15 March 2021
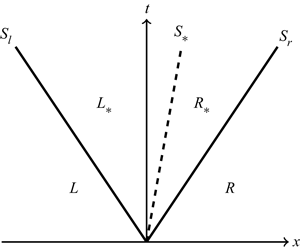
This paper presents an analytical study of the Riemann problem for dilute granular gas using initial conditions that result in a shock–contact–shock wave structure. The Euler equations for molecular gas were perturbed with small granular energy dissipation, resulting in an approximate analytical solution that is valid for early evolution time. This approximate analytical solution shows good agreement with the numerical solution of the full problem obtained using a shock-capturing scheme. It is shown that the wave structure of the Riemann problem for dilute granular gas follows that of molecular gas. However, the variables in regions between the discontinuities are functions of both space and time. Our solution shows that the ‘density overshoot’ – reported by Reddy & Alam (J. Fluid Mech., vol. 779, 2015, R2) – is not part of the shock layer but a signature of the density variation in the star region between the left and right shocks, with the maximum density occurring at the contact discontinuity.