Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T20:32:11.901Z Has data issue: false hasContentIssue false
  • English
  • Français

Single- and double-helix vortex breakdown as two dominant global modes in turbulent swirling jet flow

Published online by Cambridge University Press:  26 November 2019

Maarten Vanierschot Open the ORCID record for Maarten Vanierschot [Opens in a new window] ,
Jens S. Müller Open the ORCID record for Jens S. Müller [Opens in a new window] ,
Moritz Sieber Open the ORCID record for Moritz Sieber [Opens in a new window] ,
Mustafa Percin ,
Bas W. van Oudheusden Open the ORCID record for Bas W. van Oudheusden [Opens in a new window]  and
Kilian Oberleithner
Maarten Vanierschot*
Affiliation:
Mechanical Engineering Technology Cluster TC, Group T Leuven campus, KU Leuven, B-3000Leuven, Belgium
Jens S. Müller
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Institut für Strömungsmechanik und Technische Akustik, Technische Universität Berlin, 10623Berlin, Germany
Moritz Sieber
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Institut für Strömungsmechanik und Technische Akustik, Technische Universität Berlin, 10623Berlin, Germany
Mustafa Percin
Affiliation:
Department of Aerospace Engineering, Middle East Technical University, 06800Ankara, Turkey
Bas W. van Oudheusden
Affiliation:
Department of Aerospace Engineering, TU Delft, 2600 GBDelft, The Netherlands
Kilian Oberleithner
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Institut für Strömungsmechanik und Technische Akustik, Technische Universität Berlin, 10623Berlin, Germany
*
†Email address for correspondence: maarten.vanierschot@kuleuven.be
Get access Rights & Permissions [Opens in a new window]

Abstract

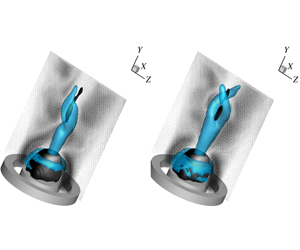
In this paper, we study the shape and dynamics of helical coherent structures found in the flow field of an annular swirling jet undergoing vortex breakdown. The flow field is studied by means of time-resolved tomographic particle image velocimetry measurements. The obtained flow fields are analysed using both classic and spectral proper orthogonal decomposition. Despite the simple geometrical set-up of the annular jet, the flow field is very complex. Two distinct large-scale helical flow structures are identified: a single and a double helix, both co-rotating with the swirl direction, and it is revealed that these structures are not higher harmonics of each other. The structures have a relatively low energy content which makes it hard to separate them from other dynamics of the flow field, notably turbulent motions. Because of this, classic proper orthogonal decomposition fails to identify both structures properly. Spectral proper orthogonal decomposition, on the other hand, allows them to be identified accurately when the filter size is set at around eight times the precession period. The precession frequencies of the single and double helices correspond to Strouhal numbers of 0.273 and $0.536\pm 0.005$, respectively. A global stability analysis of the mean flow field shows that these structures correspond to two separate global modes. The precessing frequencies obtained by the stability analysis and the related spatial structures match very well with the experimental observations. The current work extends our knowledge on turbulent vortex breakdown and on mean field global stability theory in general. It leads to the following conclusions. Firstly, single- and double-helix vortex breakdown are both manifestations of global modes. Previous studies have shown that both $m=1$ and $m=2$ modes can coexist in swirling jets. However, the $m=2$ mode has been identified as a second harmonic of the first mode, while this study identifies both as two independent global modes. Secondly, this work shows that the simultaneous occurrence of multiple helical global modes is possible within a turbulent flow and their shapes and frequencies are very well predicted by mean field stability analysis. The latter finding is of general interest as it applies to a wide class of fluid problems dominated by multiple oscillatory structures.

JFM classification

Vortex Flows: Vortex breakdown
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A31
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atkinson, C. & Soria, J. 2009 An efficient simultaneous reconstruction technique for tomographic particle image velocimetry. Exp. Fluids 47, 553.CrossRefGoogle Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.CrossRefGoogle Scholar
Beér, J. & Chigier, N. 1983 Combustion Aerodynamics. Krieger Pub Co.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14 (4), 593–629.CrossRefGoogle Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.CrossRefGoogle Scholar
Boreé, J. 2003 Extended proper orthogonal decomposition: a tool to analyse correlated events in turbulent flows. Exp. Fluids 35, 188–192.CrossRefGoogle Scholar
Brackston, R. D., García de la Cruz, J. M., Wynn, A., Rigas, G. & Morrison, J. F. 2016 Stochastic modelling and feedback control of bistability in a turbulent bluff body wake. J. Fluid Mech. 802, 726–749.CrossRefGoogle Scholar
Calderon, D. E., Wang, Z. & Gursul, I. 2012 Three-dimensional measurements of vortex breakdown. Exp. Fluids 53, 293–299.CrossRefGoogle Scholar
Canepa, E., Cattanei, A., Lengani, D., Ubaldi, M. & Zunino, P. 2015 Experimental investigation of the vortex breakdown in a lean premixing prevaporizing burner. J. Fluid Mech. 768, R4.CrossRefGoogle Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
Crouch, J. D., Garbaruk, A. & Magidov, D. 2007 Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 224 (2), 924–940.CrossRefGoogle Scholar
Crouch, J. D., Garbaruk, A., Magidov, D. & Travin, A. 2009 Origin of transonic buffet on aerofoils. J. Fluid Mech. 628, 357–369.CrossRefGoogle Scholar
Danlos, A. & Patte-Rouland, B. 2013 Experimental characterization of the initial zone of an annular jet with a very large diameter ratio. Exp. Fluids 54, 1418.CrossRefGoogle Scholar
Dinesh, K. K. J. R., Jenkins, K. W., Kirkpatrick, M. P. & Malalasekera, W. 2012 Effects of swirl on intermittency characteristics in non-premixed flames. Combust. Sci. Technol. 184 (5), 629–659.CrossRefGoogle Scholar
Dinesh, K. K. J. R. & Kirkpatrick, M. P. 2009 Study of jet precession, recirculation and vortex breakdown in turbulent swirling jets using LES. Comput. Fluids 38, 1232–1242.CrossRefGoogle Scholar
Dugué, J. & Weber, R.1992 Design and calibration of a 30 kW natural gas burner for the university of Michigan. Tech. Rep. Doc. No. C74/y/1.Google Scholar
Durao, D. F. G. & Whitelaw, J. H. 1978 Velocity characteristics of the flow in the near wake of a disk. J. Fluid Mech. 85, 369–385.CrossRefGoogle Scholar
Escudier, M. P. & Zehnder, N. 1982 Vortex-flow regimes. J. Fluid Mech. 115, 105–121.CrossRefGoogle Scholar
Falese, M., Gicquel, L. Y. & Poinsot, T. 2014 LES of bifurcation and hysteresis in confined annular swirling flows. Comput. Fluids 89, 167–178.CrossRefGoogle Scholar
Gallaire, F., Rott, S. & Chomaz, J.-M. 2004 Experimental study of a free and forced swirling jet. Phys. Fluids 16, 2907–2917.CrossRefGoogle Scholar
Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.CrossRefGoogle Scholar
Garcia-Villalba, M. & Frohlich, J. 2006 Les of a free annular swirling jet – dependence of coherent structures on a pilot jet and the level of swirl. Intl J. Heat Fluid Flow 27, 911–923.CrossRefGoogle Scholar
Garcia-Villalba, M., Frohlich, J. & Rodi, W. 2006 Identification and analysis of coherent structures in the near field of a turbulent unconfined annular swirling jet using large eddy simulation. Phys. Fluids 18, 055103.CrossRefGoogle Scholar
Gentille, V., van Oudheusden, B. W., Schrijer, F. F. J. & Scarano, F. 2017 The effect of angular misalignment on low-frequency axisymmetric wake instability. J. Fluid Mech. 813, R3.CrossRefGoogle Scholar
Gentille, V., Schrijer, F. F. J., van Oudheusden, B. W. & Scarano, F. 2016 Low-frequency behavior of the turbulent axisymmetric near-wake. Phys. Fluids 28, 065102.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013 Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.CrossRefGoogle Scholar
Gupta, A. & Lilley, G. 1984 Swirl Flows. Abacus, Kent.Google Scholar
Huang, Y., Sung, H. G., Hsieh, S. Y. & Yang, V. 2003 Large-eddy simulation of combustion dynamics of lean-premixed swirl-stabilized combustor. J. Propul. Power 19, 782–794.CrossRefGoogle Scholar
Huang, Y. & Yang, V. 2005 Effect of swirl on combustion dynamics in a lean-premixed swirl-stabilized combustor. Proc. Combust. Inst. 30, 1775–1782.CrossRefGoogle Scholar
Hussain, A. K. M. F. & Reynolds, W. C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41, 241–258.CrossRefGoogle Scholar
Ivanova, E. M., Noll, B. E. & Aigner, M. 2013 A numerical study on the turbulent Schmidt numbers in a jet in crossflow. Trans. ASME J. Engng Gas Turbines Power 135 (1), 011505.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jones, W. P., Lyra, S. & Navarro-Martinex, S. 2012 Large eddy simulation of turbulent confined highly swirling annular flows. Flow Turbul. Combust. 89, 361–384.CrossRefGoogle Scholar
Kaiser, T. L., Poinsot, T. & Oberleithner, K. 2017 Stability and sensitivity analysis of hydrodynamic instabilities in industrial swirled injection systems. In ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition. American Society of Mechanical Engineers.Google Scholar
Ko, N. W. M. & Chan, W. T. 1979 Inner regions of annular jets. J. Fluid Mech. 93, 549–584.CrossRefGoogle Scholar
Lambourne, N. C. & Bryer, D. W.1961 The bursting of leading-edge vortices: some observations and discussion of the phenomenon. Tech. Rep. 3282. Ministry of Aviation, Aeronautical Research Council.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.CrossRefGoogle Scholar
Lucas, J.-M., Cadot, O., Herbert, V., Parpais, S. & Delery, J. 2017 A numerical investigation of the asymmetric wake mode of a squareback Ahmed body – effect of a base cavity. J. Fluid Mech. 831, 675–697.CrossRefGoogle Scholar
Lucca-Negro, O. & O’Doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27, 431–481.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.CrossRefGoogle Scholar
Lumley, J. L. 1970 Stochastic Tools in Turbulence, Applied Mathematics and Mechanics Series: vol. 12. Academic Press.Google Scholar
Mantič-Lugo, V., Arratia, C. & Gallaire, F. 2015 A self-consistent model for the saturation dynamics of the vortex shedding around the mean flow in the unstable cylinder wake. Phys. Fluids 27 (7), 074103.CrossRefGoogle Scholar
Matas, J.-P., Delon, A. & Cartellier, A. 2018 Shear instability of an axisymmetric air–water coaxial jet. J. Fluid Mech. 843, 575–600.CrossRefGoogle Scholar
Meliga, P., Cadot, V. & Serre, E. 2016 Experimental and theoretical sensitivity analysis of turbulent flow past a square cylinder. Flow Turbul. Combust. 97 (4), 987–1015.CrossRefGoogle Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012a A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.CrossRefGoogle Scholar
Meliga, P., Pujals, G. & Serre, E. 2012b Sensitivity of 2-D turbulent flow past a D-shaped cylinder using global stability. Phys. Fluids 24 (6), 061701.CrossRefGoogle Scholar
Mettot, C., Sipp, D. & Bézard, H. 2014 Quasi-laminar stability and sensitivity analyses for turbulent flows: prediction of low-frequency unsteadiness and passive control. Phys. Fluids 26 (4), 045112.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C. O., Seele, R. & Wygnanski, I. 2012 Formation of turbulent vortex breakdown: intermittency, criticality, and global instability. AIAA J. 50 (7), 1437–1452.CrossRefGoogle Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H. C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.CrossRefGoogle Scholar
Oberleithner, K., Stöhr, M., Seong, H. I., Arndt, C. M. & Steinberg, A. M. 2015 Formation and flame-induced supression of the precessing vortex core in a swirl combustor: experiments and linear stability analysis. Combust. Flame 162 (8), 3100–3114.CrossRefGoogle Scholar
O’Connor, J. & Lieuwen, T. 2012 Recirculation zone dynamics of a transversal excited swirl flow and flame. Phys. Fluids 24, 075107.CrossRefGoogle Scholar
Paredes, P.2014 Advances in global instability computations: from incompressible to hypersonic flow. PhD thesis, Technical University of Madrid.Google Scholar
Patte-Rouland, B., Lalizel, G., Moreau, J. & Rouland, E. 2001 Flow analysis of an annular jet by particle image velocimetry and proper orthogonal decomposition. Meas. Sci. Technol. 12, 1404–1412.CrossRefGoogle Scholar
Pavia, G., Passmore, M. & Sardu, C. 2018 Evolution of the bi-stable wake of a square-back automotive shape. Exp. Fluids 59, 20.CrossRefGoogle Scholar
Percin, M., Vanierschot, M. & van Oudheusden, B. W. 2017 Analysis of the pressure fields in a swirling annular jet flow. Exp. Fluids 58, 166.CrossRefGoogle Scholar
Poinsot, T. 2017 Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst. 36, 1–28.CrossRefGoogle Scholar
Qadri, U. A., Mistry, D. & Juniper, M. P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.CrossRefGoogle Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.CrossRefGoogle Scholar
Rigas, G., Morgans, A. S., Brackston, R. D. & Morrison, J. F. 2015 Diffusive dynamics and stochastic models of turbulent axisymmetric wakes. J. Fluid Mech. 778, R2.CrossRefGoogle Scholar
Rigas, G., Oxlade, A. R., Morgans, A. S. & Morrison, J. F. 2014 Low-dimensional dynamics of a turbulent axisymmetric wake. J. Fluid Mech. 755, R5.CrossRefGoogle Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Ruith, M., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
Rukes, L., Paschereit, C. O. & Oberleithner, K. 2016 An assessment of turbulence models for linear hydrodynamic stability analysis of strongly swirling jets. Eur. J. Mech. (B/Fluids) 59, 205–218.CrossRefGoogle Scholar
Rukes, L., Sieber, M., Paschereit, C. O. & Oberleithner, K. 2017 Transient evolution of the global mode in turbulent swirling jets: experiments and modal stability analysis. Eur. J. Mech. (B/Fluids) 65, 98–106.CrossRefGoogle Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45, 545–559.CrossRefGoogle Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Sheen, H., Chen, W. & Jeng, S. 1996 Recirculation zones of unconfined and confined annular swirling jets. AIAA J. 34, 572–579.CrossRefGoogle Scholar
Sieber, M., Paschereit, C. O. & Oberleithner, K. 2016 Spectral proper orthogonal decomposition. J. Fluid Mech. 792, 798–828.CrossRefGoogle Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 030801.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I. Coherent structures. Q. Appl. Maths 45, 561–571.CrossRefGoogle Scholar
Stoehr, M., Boxx, I. & Campbell, C. D. 2012 Experimental study of vortex-flame interaction in a gas turbine model combustor. Combust. Flame 159, 2636–2649.CrossRefGoogle Scholar
Syred, N. 2006 A review of oscillation mechanisms and the role of the precessing vortex core (pvc) in swirl combustion systems. Prog. Energy Combust. Sci. 32 (2), 93–161.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Terhaar, S., Oberleithner, K. & Paschereit, C. O. 2015 Key parameters governing the precessing vortex core in reacting flows: an experimental and analytical study. Proc. Combust. Inst. 35 (3), 3347–3354.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
Theofilis, V., Duck, P. W. & Owen, J. 2004 Viscous linear stability analysis of rectangular duct and cavity flows. J. Fluid Mech. 505, 249–286.CrossRefGoogle Scholar
Turton, S. E., Tuckerman, L. S. & Barkley, D. 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E 91 (4), 043009.Google ScholarPubMed
Vadivukkarasan, M. & Panchagnula, M. V. 2017 Combined Rayleigh–Taylor and Kelvin–Helmholtz instabilities on an annular liquid sheet. J. Fluid Mech. 812, 152–177.CrossRefGoogle Scholar
Vanierschot, M. 2017 On the dynamics of the transition to vortex breakdown in axisymmetric inviscid swirling flows. Eur. J. Mech. (B/Fluids) 65, 65–69.CrossRefGoogle Scholar
Vanierschot, M., Percin, M. & van Oudheusden, B. W. 2018 Double helix vortex breakdown in a turbulent swirling annular jet flow. Phys. Rev. Fluids 3, 034703.CrossRefGoogle Scholar
Vanierschot, M. & Van den Bulck, E. 2008 Influence of swirl on the initial merging zone of a turbulent annular jet. Phys. Fluids 20, 105104.CrossRefGoogle Scholar
Vanierschot, M. & Van den Bulck, E. 2011 Experimental study of low precessing frequencies in the wake of a turbulent annular jet. Exp. Fluids 50, 189–200.CrossRefGoogle Scholar
Vanierschot, M., Van Dyck, K., Sas, P. & Van den Bulck, E. 2014 Symmetry breaking and vortex precession in low-swirling annular jets. Phys. Fluids 26, 105110.CrossRefGoogle Scholar
Wieneke, B. 2008 Volume self-calibration for 3d particle image velocimetry. Exp. Fluids 45, 549–556.CrossRefGoogle Scholar
Williams, M. O., Kevrekidis, I. G. & Rowley, C. W. 2015 A data-driven approximation of the koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25, 1307–1346.CrossRefGoogle Scholar
Zhang, H. D., Han, C., Ye, T. H., Zhang, J. M. & Chen, Y. 2015 Large eddy simulation of unconfined turbulent swirling flow. Sci. China Technol. Sci. 58, 1731–1744.CrossRefGoogle Scholar