Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Machicoane, Nathanaël
Zimmermann, Robert
Fiabane, Lionel
Bourgoin, Mickaël
Pinton, Jean-François
and
Volk, Romain
2014.
Large sphere motion in a nonhomogeneous turbulent flow.
New Journal of Physics,
Vol. 16,
Issue. 1,
p.
013053.
Uhlmann, Markus
and
Doychev, Todor
2014.
Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion.
Journal of Fluid Mechanics,
Vol. 752,
Issue. ,
p.
310.
Tanaka, M.
and
Teramoto, D.
2015.
Modulation of homogeneous shear turbulence laden with finite-size particles.
Journal of Turbulence,
Vol. 16,
Issue. 10,
p.
979.
Cisse, M.
Saw, E.-W.
Gibert, M.
Bodenschatz, E.
and
Bec, J.
2015.
Turbulence attenuation by large neutrally buoyant particles.
Physics of Fluids,
Vol. 27,
Issue. 6,
Homann, H.
Guillot, T.
Bec, J.
Ormel, C. W.
Ida, S.
and
Tanga, P.
2016.
Effect of turbulence on collisions of dust particles with planetesimals in protoplanetary disks.
Astronomy & Astrophysics,
Vol. 589,
Issue. ,
p.
A129.
Zhdanov, S.
Du, C.-R.
Schwabe, M.
Nosenko, V.
Thomas, H. M.
and
Morfill, G. E.
2016.
Wake turbulence observed behind an upstream “extra” particle in a complex (dusty) plasma.
EPL (Europhysics Letters),
Vol. 114,
Issue. 5,
p.
55002.
Brändle de Motta, J.C.
Estivalezes, J.L.
Climent, E.
and
Vincent, S.
2016.
Local dissipation properties and collision dynamics in a sustained homogeneous turbulent suspension composed of finite size particles.
International Journal of Multiphase Flow,
Vol. 85,
Issue. ,
p.
369.
Fornari, Walter
Picano, Francesco
and
Brandt, Luca
2016.
Sedimentation of finite-size spheres in quiescent and turbulent environments.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
640.
Fornari, Walter
Picano, Francesco
Sardina, Gaetano
and
Brandt, Luca
2016.
Reduced particle settling speed in turbulence.
Journal of Fluid Mechanics,
Vol. 808,
Issue. ,
p.
153.
Homann, Holger
2017.
Collective Dynamics of Particles.
Vol. 576,
Issue. ,
p.
39.
Luo, Kun
Wang, Zhuo
Li, Dong
Tan, Junhua
and
Fan, Jianren
2017.
Fully resolved simulations of turbulence modulation by high-inertia particles in an isotropic turbulent flow.
Physics of Fluids,
Vol. 29,
Issue. 11,
p.
113301.
Loisy, Aurore
and
Naso, Aurore
2017.
Interaction between a large buoyant bubble and turbulence.
Physical Review Fluids,
Vol. 2,
Issue. 1,
Lin, Zhaowu
Yu, Zhaosheng
Shao, Xueming
and
Wang, Lian-Ping
2017.
Effects of finite-size neutrally buoyant particles on the turbulent flows in a square duct.
Physics of Fluids,
Vol. 29,
Issue. 10,
Xia, Junjie
Luo, Kun
and
Fan, Jianren
2017.
Fully resolved numerical simulation of interphase heat transfer in gas–solid turbulent flow.
International Journal of Heat and Mass Transfer,
Vol. 112,
Issue. ,
p.
45.
Tanaka, Mitsuru
2017.
Effect of gravity on the development of homogeneous shear turbulence laden with finite-size particles.
Journal of Turbulence,
Vol. 18,
Issue. 12,
p.
1144.
Traugott, Hadar
and
Liberzon, Alex
2017.
Experimental study of forces on freely moving spherical particles during resuspension into turbulent flow.
International Journal of Multiphase Flow,
Vol. 88,
Issue. ,
p.
167.
Yu, Zhaosheng
Lin, Zhaowu
Shao, Xueming
and
Wang, Lian-Ping
2017.
Effects of particle-fluid density ratio on the interactions between the turbulent channel flow and finite-size particles.
Physical Review E,
Vol. 96,
Issue. 3,
Uhlmann, Markus
and
Chouippe, Agathe
2017.
Clustering and preferential concentration of finite-size particles in forced homogeneous-isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
991.
Bounoua, S.
Bouchet, G.
and
Verhille, G.
2018.
Tumbling of Inertial Fibers in Turbulence.
Physical Review Letters,
Vol. 121,
Issue. 12,
Lalescu, Cristian C.
and
Wilczek, Michael
2018.
Acceleration statistics of tracer particles in filtered turbulent fields.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
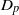 ${D}_{p} $. Finally, asymptotic arguments are used to relate the viscous sublayer quantities to the particle size and the properties of the outer turbulence. It is shown in particular that the skin-friction Reynolds number behaves as
${D}_{p} $. Finally, asymptotic arguments are used to relate the viscous sublayer quantities to the particle size and the properties of the outer turbulence. It is shown in particular that the skin-friction Reynolds number behaves as  $R{e}_{\tau } \propto {({D}_{p} / \eta )}^{4/ 3} $.
$R{e}_{\tau } \propto {({D}_{p} / \eta )}^{4/ 3} $.

