Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T13:12:17.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability transitions and turbulence in horizontal convection

Published online by Cambridge University Press:  25 June 2014

Bishakhdatta Gayen ,
Ross W. Griffiths  and
Graham O. Hughes
Bishakhdatta Gayen*
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 0200, Australia
Ross W. Griffiths
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 0200, Australia
Graham O. Hughes
Affiliation:
Research School of Earth Sciences, The Australian National University, Canberra, ACT 0200, Australia
*
†Email address for correspondence: bishakhdatta.gayen@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent results have shown that convection forced by a temperature gradient along one horizontal boundary of a rectangular domain at a large Rayleigh number can be turbulent in parts of the flow field. However, the conditions for onset of turbulence, the dependence of flow and heat transport on Rayleigh number, and the roles of large and small scales in the flow, have not been established. We use three-dimensional direct numerical simulation (DNS) and large-eddy simulation (LES) over a wide range of Rayleigh numbers, 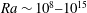$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Ra\sim 10^8\mbox{--}10^{15}$, for Prandtl number 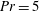$Pr=5$ and a small aspect ratio, and show that a sequence of several stability transitions at 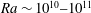$Ra \sim 10^{10}\mbox{--} 10^{11}$ defines a change from laminar to turbulent flow. The Prandtl number dependence too is examined at 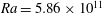$Ra = 5.86 \times 10^{11}$. At the smallest 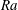$Ra$ considered the thermal boundary layer is characterized by a balance of viscous stress and buoyancy, whereas inertia and buoyancy dominate in the large-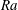$Ra$ regime. The change in the momentum balance is accompanied by turbulent enhancement of the overall heat transfer, although both laminar and turbulent regimes give 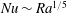$Nu\sim Ra^{1/5}$. The results support both viscous and inviscid theoretical scaling models from previous work. The mechanical energy budget for an intermediate range of Rayleigh numbers above onset of instability (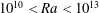$10^{10}<Ra<10^{13}$) reveals that the small scales of motion are produced predominantly by thermal convection, whereas at 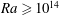$Ra \ge 10^{14}$ shear instability of the large-scale flow begins to play a dominant role in sustaining the small-scale turbulence. Extrapolation to ocean conditions requires knowledge of the inertial regime identified here, but the simulations show that the corresponding asymptotic balance has not been fully realized by 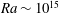$Ra \sim 10^{15}$.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection Geophysical and Geological Flows: Ocean circulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 698 - 724
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1–42.Google Scholar
Barkan, R., Winters, K. B. & Llewellyn Smith, S. 2013 Rotating horizontal convection. J. Fluid Mech. 723, 556–586.Google Scholar
Chiu-Webster, S., Hinch, E. J. & Lister, J. R. 2008 Very viscous horizontal convection. J. Fluid Mech. 611, 395–426.Google Scholar
Gayen, B., Griffiths, R. W., Hughes, G. O. & Saenz, J. A. 2013a Energetics of horizontal convection. J. Fluid Mech. 716, R10.Google Scholar
Gayen, B., Hughes, G. O. & Griffiths, R. W. 2013b Completing the mechanical energy pathways in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 111, 124301.Google Scholar
Gayen, B. & Sarkar, S. 2010 Turbulence during the generation of internal tide on a critical slope. Phys. Rev. Lett. 104, 218502.CrossRefGoogle ScholarPubMed
Gayen, B. & Sarkar, S. 2011 Direct and large eddy simulations of internal tide generation at a near critical slope. J. Fluid Mech. 681, 48–79.Google Scholar
Gayen, B., Sarkar, S. & Taylor, J. R. 2010 Large eddy simulation of a stratified boundary layer under an oscillatory current. J. Fluid Mech. 643, 233–266.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 3 (7), 1760–1765.Google Scholar
Griffiths, R. W., Hughes, G. O. & Gayen, B. 2013 Horizontal convection dynamics: insights from transient adjustment. J. Fluid Mech. 726, 559–595.Google Scholar
Holford, J. M. & Linden, P. F. 1999 Turbulent mixing in a stratified fluid. Dyn. Atmos. Oceans 30, 173–198.Google Scholar
Hughes, G. O., Gayen, B. & Griffiths, R. W. 2013 Available potential energy in Rayleigh–Bénard convection. J. Fluid Mech. 729, 1–10; R3.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2006 A simple convective model of the global overturning circulation, including effects of entrainment into sinking regions. Ocean Model. 12, 46–79.CrossRefGoogle Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.CrossRefGoogle Scholar
Hughes, G. O., Griffiths, R. W., Mullarney, J. C. & Peterson, W. H. 2007 A theoretical model for horizontal convection at high Rayleigh number. J. Fluid Mech. 581, 251–276.CrossRefGoogle Scholar
Hughes, G. O., Hogg, A. McC. & Griffiths, R. W. 2009 Available potential energy and irreversible mixing in the meridional overturning circulation. J. Phys. Oceanogr. 39, 3130–3146.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13, 3–23.CrossRefGoogle Scholar
Lund, T. S.1997 On the use of discrete filters for large eddy simulation. In Annual Research Briefs, pp. 83–95. Centre for Turbulence Research, NASA Ames–Stanford University.Google Scholar
Mullarney, J. C., Griffiths, R. W. & Hughes, G. O. 2004 Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209.Google Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2011 Local energy dissipation rate balances local heat flux in the centre of turbulent thermal convection. Phys. Rev. Lett. 107, 174503.CrossRefGoogle ScholarPubMed
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.Google Scholar
Paparella, F. & Young, W. R. 2002 Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214.CrossRefGoogle Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Prastowo, T., Griffiths, R. W., Hughes, G. O. & Hogg, A. McC. 2008 Mixing efficiency in controlled exchange flows. J. Fluid Mech. 600, 235–244.CrossRefGoogle Scholar
Prastowo, T., Griffiths, R. W., Hughes, G. O. & Hogg, A. M. C. 2009 Effects of topography on the cumulative mixing efficiency in exchange flows. J. Geophys. Res. 114 (C8), C08008.Google Scholar
Rossby, H. T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep-Sea Res. 12, 9–16.Google Scholar
Rossby, H. T. 1998 Numerical experiments with a fluid heated non-uniformly from below. Tellus A 50, 242–257.Google Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really non-turbulent? Geophys. Res. Lett. 38, L21609.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.Google Scholar
Stewart, K. D., Hughes, G. O. & Griffiths, R. W. 2011 When do marginal seas and topographic sills modify the ocean density structure? J. Geophys. Res. 116, C08021.Google Scholar
Stommel, H. 1962 On the smallness of sinking regions in the ocean. Proc. Natl Acad. Sci. USA 48, 766–772.Google Scholar
Tailleux, R. 2009 On the energetics of stratified turbulent mixing, irreversible thermodynamics, Boussinesq models and the ocean heat engine controversy. J. Fluid Mech. 638, 339–382.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Vreman, B., Geurts, B. & Kuerten, H. 1997 Large-eddy simulation of the turbulent mixing layer. J. Fluid Mech. 339, 357–390.Google Scholar
Winters, K. B. & D’Asaro, E. A. 1994 Three-dimensional wave instability near a critical level. J. Fluid Mech. 272, 255–284.CrossRefGoogle Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Winters, K. B. & Young, W. R. 2009 Available potential energy and buoyancy variance in horizontal convection. J. Fluid Mech. 629, 221–230.Google Scholar
Zang, Y., Street, R. L. & Koseff, J. R. 1993 A dynamic mixed subgrid-scale model and its application to turbulent recirculating flows. Phys. Fluids A 5 (12), 3186–3196.CrossRefGoogle Scholar