Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Long-Wei
Pan, Chong
and
Wang, Jin-Jun
2022.
Wall-attached and wall-detached eddies in proper orthogonal decomposition modes of a turbulent channel flow.
Physics of Fluids,
Vol. 34,
Issue. 9,
Wu, Gen
Fang, Le
and
Zhang, Jin
2022.
Numerical investigation and parametric analysis of an attached eddy model applied to inlet condition.
Physics of Fluids,
Vol. 34,
Issue. 11,
2023.
Reduced-order representation of superstructures in a turbulent boundary layer.
Physics of Fluids,
Vol. 35,
Issue. 5,
Hu, Ruifeng
Dong, Siwei
and
Vinuesa, Ricardo
2023.
General attached eddies: Scaling laws and cascade self-similarity.
Physical Review Fluids,
Vol. 8,
Issue. 4,
He, Kang-jian
Zhou, Fu-chang
Zhao, Wei-wen
Wang, Jian-hua
and
Wan, De-cheng
2023.
Numerical analysis of turbulent fluctuations around an axisymmetric body of revolution based on wall-modeled large eddy simulations.
Journal of Hydrodynamics,
Vol. 35,
Issue. 6,
p.
1041.
Feng, Zhixiang
and
Ye, Qingqing
2023.
Turbulent boundary layer over porous media with wall-normal permeability.
Physics of Fluids,
Vol. 35,
Issue. 9,
Liu, Yaoyao
Pan, Chong
and
Liu, Jianhua
2023.
Intermittent behavior of a bypass transition of boundary layers over an axisymmetric body of revolution.
Ocean Engineering,
Vol. 286,
Issue. ,
p.
115689.
Dong, Zhen-xun
Pan, Chong
Tong, Fu-lin
and
Yuan, Xian-xu
2024.
Variation of vortical structures across shock-wave/turbulent boundary-layer interaction region in a compression ramp flow.
Physics of Fluids,
Vol. 36,
Issue. 5,
Freeman, Benjamin R.S.
Martinuzzi, Robert J.
and
Hemmati, Arman
2024.
Momentum analysis of complex time-periodic flows.
Journal of Fluid Mechanics,
Vol. 979,
Issue. ,
Feng, Yuen
Liu, Hongyou
and
Zheng, Xiaojing
2024.
The modulation of coherent structures by the near-wall motions of particles.
Journal of Fluid Mechanics,
Vol. 981,
Issue. ,
Long, Wenxiao
Xiong, Dapeng
Wang, Hongbo
Sun, Mingbo
Chen, Huifeng
Li, Wenming
and
Yang, Yixin
2024.
Generation of inflow turbulence using an improved synthetic eddy method.
Physics of Fluids,
Vol. 36,
Issue. 8,
Li, X. X.
Hu, R. F.
and
Fang, L.
2024.
Scaling laws of velocity gradient moments of attached eddies.
Physical Review Fluids,
Vol. 9,
Issue. 9,
Zhang, Yi
Pan, Chong
Wang, Jinjun
and
Zhang, Miao
2024.
Modulating multi-scale motions in a turbulent boundary layer by micro vortex generators.
Physics of Fluids,
Vol. 36,
Issue. 8,
Massaro, D.
Yao, J.
Rezaeiravesh, S.
Hussain, F.
and
Schlatter, P.
2024.
Karhunen–Loéve decomposition of high Reynolds number turbulent pipe flows: a Voronoi analysis.
Journal of Physics: Conference Series,
Vol. 2753,
Issue. 1,
p.
012018.
Liu, Yaoyao
Pan, Chong
Zhang, Qingfu
and
Liu, Jianhua
2024.
Multi-scale characteristics and inter-scale interaction in a transitional boundary layer over an axisymmetric body of revolution.
Physics of Fluids,
Vol. 36,
Issue. 8,
He, Xibo
Liu, Hongyou
and
Zheng, Xiaojing
2024.
Self-scaling generalized Townsend-Perry constants for high-order moments in turbulent boundary layers.
Physical Review Fluids,
Vol. 9,
Issue. 8,
Wang, Ping
Zhou, Zhiqi
Chen, Zhizong
Sung, Hyung Jin
Liu, Yuan
and
Wu, Jianjun
2024.
Turbulent boundary layer structures downstream of a square cylinder.
Physics of Fluids,
Vol. 36,
Issue. 8,
He, Kangjian
Pan, Zhi
Zhao, Weiwen
Wang, Jianhua
and
Wan, Decheng
2024.
Overview of Research Progress on Numerical Simulation Methods for Turbulent Flows Around Underwater Vehicles.
Journal of Marine Science and Application,
Vol. 23,
Issue. 1,
p.
1.
Chen, Letian
Tang, Zhanqi
Fan, Ziye
and
Jiang, Nan
2024.
Outer-layer self-similarity of the turbulent boundary layer based on the turbulent/non-turbulent interface.
Physical Review Fluids,
Vol. 9,
Issue. 3,
Massaro, D.
Yao, J.
Rezaeiravesh, S.
Hussain, F.
and
Schlatter, P.
2024.
Energy-based characterisation of large-scale coherent structures in turbulent pipe flows.
Journal of Fluid Mechanics,
Vol. 996,
Issue. ,
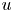 $u$ component wall-attached eddies in proper orthogonal decomposition modes of a turbulent boundary layer
$u$ component wall-attached eddies in proper orthogonal decomposition modes of a turbulent boundary layer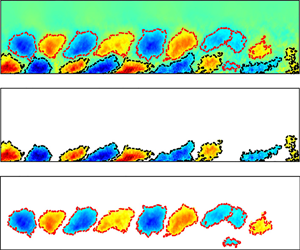
 $u$ component velocity fields in the streamwise–wall-normal plane of three turbulent boundary layers, which cover a frictional Reynolds number (
$u$ component velocity fields in the streamwise–wall-normal plane of three turbulent boundary layers, which cover a frictional Reynolds number ( $Re$) of
$Re$) of  $Re_\tau \approx 1000{\sim} 4000$ and were either measured by large-field-of-view planar particle image velocimetry or calculated by direct numerical simulation. The
$Re_\tau \approx 1000{\sim} 4000$ and were either measured by large-field-of-view planar particle image velocimetry or calculated by direct numerical simulation. The  $u$ component POD modes characterized by streamwise recurring large-scale motions are decomposed into wall-attached and wall-detached parts depending on the wall-attachment condition. The former, i.e. wall-attached POD eddies, are believed to be the prime statistical representations of attached eddies. The reason lies in three aspects. Firstly, wall-attached POD eddies are geometrically self-similar and statistically independent. Secondly, the wall-normal variation of the variance of reduced-order streamwise velocity components
$u$ component POD modes characterized by streamwise recurring large-scale motions are decomposed into wall-attached and wall-detached parts depending on the wall-attachment condition. The former, i.e. wall-attached POD eddies, are believed to be the prime statistical representations of attached eddies. The reason lies in three aspects. Firstly, wall-attached POD eddies are geometrically self-similar and statistically independent. Secondly, the wall-normal variation of the variance of reduced-order streamwise velocity components  $\tilde {u}_{AE}$, which is only contributed by wall-attached POD eddies, presents logarithmic decay in the inertial flow region. Thirdly, analysis on the scaling behaviour of the high-even-order moment, moment generating function, as well as longitudinal two-point structure function, all indicate a quasi-Gaussian behaviour of
$\tilde {u}_{AE}$, which is only contributed by wall-attached POD eddies, presents logarithmic decay in the inertial flow region. Thirdly, analysis on the scaling behaviour of the high-even-order moment, moment generating function, as well as longitudinal two-point structure function, all indicate a quasi-Gaussian behaviour of  $\tilde {u}_{AE}$. None of these AEH-predicted behaviours are evident when the contribution of superstructure-like POD eddies are considered. Furthermore, wall-detached POD eddies are found to also present quasi-Gaussian behaviour. They might be treated as passive fragments of wall-attached ones.
$\tilde {u}_{AE}$. None of these AEH-predicted behaviours are evident when the contribution of superstructure-like POD eddies are considered. Furthermore, wall-detached POD eddies are found to also present quasi-Gaussian behaviour. They might be treated as passive fragments of wall-attached ones.