Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-29T05:38:49.693Z Has data issue: false hasContentIssue false
  • English
  • Français

A stochastic model for the relative motion of high Stokes number particles in isotropic turbulence

Published online by Cambridge University Press:  05 September 2014

Sarma L. Rani ,
Rohit Dhariwal  and
Donald L. Koch
Sarma L. Rani*
Affiliation:
Mechanical and Aerospace Engineering Department, University of Alabama in Huntsville, Huntsville, AL 35899, USA
Rohit Dhariwal
Affiliation:
Mechanical and Aerospace Engineering Department, University of Alabama in Huntsville, Huntsville, AL 35899, USA
Donald L. Koch
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: sarma.rani@uah.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The probability density function (PDF) kinetic equation describing the relative motion of inertial particle pairs in a turbulent flow requires closure of the phase-space diffusion current. A novel analytical closure for the diffusion current is presented that is applicable to high-inertia particle pairs with Stokes numbers 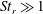$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathit{St}}_r \gg 1$. Here 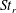${\mathit{St}}_r$ is a Stokes number based on the time scale 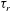$\tau _r$ of eddies whose size scales with pair separation $r$. In the asymptotic limit of 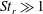${\mathit{St}}_r \gg 1$, the pair PDF kinetic equation reduces to an equation of Fokker–Planck form. The diffusion tensor characterizing the diffusion current in the Fokker–Planck equation is equal to 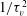$1/\tau _v^2$ multiplied by the time integral of the Lagrangian correlation of fluid relative velocities along particle-pair trajectories. Here, 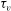$\tau _v$ is the particle viscous relaxation time. Closure of the diffusion tensor is achieved by converting the Lagrangian correlations of fluid relative velocities ‘seen’ by pairs into Eulerian fluid-velocity correlations at pair separations that remain essentially constant during time scales of 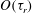$O(\tau _r)$; the pair centre of mass, however, is not stationary and responds to eddies with time scales comparable to or smaller than 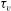$\tau _v$. For isotropic turbulence, Eulerian fluid-velocity correlations may be expressed as Fourier transforms of the velocity spectrum tensor, enabling us to derive a closed-form expression for the diffusion tensor. A salient feature of this closure is that it has a single, unique form for pair separations spanning the entire spectrum of turbulence scales, unlike previous closures that involve velocity structure functions with different forms for the integral, inertial subrange, and Kolmogorov-scale separations. Using this closure, Langevin equations, which are statistically equivalent to the Fokker–Planck equation, were solved to evolve particle-pair relative velocities and separations in stationary isotropic turbulence. The Langevin equation approach enables the simulation of the full PDF of pair relative motion, instead of only the first few moments of the PDF as is the case in a moments-based approach. Accordingly, PDFs 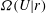$\varOmega (U|r)$ and 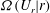$\varOmega (U_r|r)$ are computed and presented for various separations $r$, where the former is the PDF of relative velocity 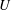$U$ and the latter is the PDF of the radial component of relative velocity 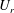$U_r$, both conditioned upon the separation $r$. Consistent with the direct numerical simulation (DNS) study of Sundaram & Collins (J. Fluid Mech., vol. 335, 1997, pp. 75–109), the Langevin simulations capture the transition of 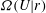$\varOmega (U|r)$ from being Gaussian at integral-scale separations to an exponential PDF at Kolmogorov-scale separations. The radial distribution functions (RDFs) computed from these simulations also show reasonable quantitative agreement with those from the DNS study of Février, Simonin & Legendre (Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, 2001).

JFM classification

Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 870 - 902
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayala, O., Rosa, B. & Wang, L.-P. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 2. Theory and parameterization. New J. Phys. 10, 1–40.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Bixon, M. & Zwanzig, R. 2005 Boltzmann–Langevin equation and hydrodynamic fluctuations. Phys. Rev. 187, 267–272.Google Scholar
Bragg, A., Swailes, D. C. & Skartlien, R. 2012 Drift-free kinetic equations for turbulent dispersion. Phys. Rev. E 86, 056306.CrossRefGoogle ScholarPubMed
Buyevich, Yu. A. 1971 Statistical hydromechanics of disperse systems. Part 1. Physical background and general equations. J. Fluid Mech. 49, 489–507.Google Scholar
Buyevich, Yu. A. 1972a Statistical hydromechanics of disperse systems. Part 2. Solution of the kinetic equation for suspended particles. J. Fluid Mech. 52, 345–355.Google Scholar
Buyevich, Yu. A. 1972b Statistical hydromechanics of disperse systems. Part 3. Pseudo-turbulent structure of homogeneous suspensions. J. Fluid Mech. 56, 313–336.Google Scholar
Chiang, E. & Youdin, A. 2005 Forming planetesimals in solar and extrasolar nebulae. Annu. Rev. Earth Planet. Sci. 38, 493–522.Google Scholar
Chun, J., Koch, D. L., Rani, S. L., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.Google Scholar
Derevich, I. V. 2006 Statistical modeling of particles relative motion in a turbulent gas flow. Intl J. Heat Mass Transfer 49, 4290–4304.CrossRefGoogle Scholar
Druzhinin, O. A. 1995 On the two-way interaction in two-dimensional particle-laden flows: the accumulation of particles and flow modification. J. Fluid Mech. 297, 49–76.Google Scholar
Druzhinin, O. A. & Elghobashi, S. 1999 On the decay rate of isotropic turbulence laden with microparticles. Phys. Fluids 11, 602–610.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Ferry, J. & Balachandar, S. 2001 A fast Eulerian method for disperse two-phase flow. Intl J. Multiphase Flow 27, 1199–1226.Google Scholar
Ferry, J., Rani, S. L. & Balachandar, S. 2003 A locally implicit improvement of the equilibrium Eulerian method. Intl J. Multiphase Flow 29, 869–891.CrossRefGoogle Scholar
Février, P., Simonin, O. & Legendre, D.2001 Particle dispersion and preferential concentration dependence on turbulent Reynolds number from direct and large-eddy simulations of isotropic homogeneous turbulence. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans.Google Scholar
Gardiner, C. W. 1990 Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. Springer.Google Scholar
Goswami, P. S. & Kumaran, V. 2010a Particle dynamics in a turbulent particle-gas suspension at high Stokes number. Part 1. Velocity and acceleration distributions. J. Fluid Mech. 646, 59–90.CrossRefGoogle Scholar
Goswami, P. S. & Kumaran, V. 2010b Particle dynamics in a turbulent particle-gas suspension at high Stokes number. Part 2. The fluctuating-force model. J. Fluid Mech. 646, 91–125.Google Scholar
Gualtieri, P., Casciola, C. M., Benzi, R., Amati, G. & Piva, R. 2002 Scaling laws and intermittency in homogeneous shear flow. Phys. Fluids 14 (2), 583–596.Google Scholar
Huber, G. A. & Kim, S. 1996 Weighted-ensemble Brownian dynamics simulations for protein association reactions. Biophys. J. 70, 97–110.CrossRefGoogle ScholarPubMed
Hyland, K. E., McKee, S. & Reeks, M. W. 1999 Derivation of a pdf kinetic equation for the transport of particles in turbulent flows. J. Phys. A: Math. Gen. 32, 6169–6190.CrossRefGoogle Scholar
Jung, J., Yeo, K. & Lee, C. 2008 Behavior of heavy particles in isotropic turbulence. Phys. Rev. E 77, 016307.Google Scholar
Kelly, G. E. & Lewis, M. B. 1971 Hydrodynamic fluctuations. Phys. Fluids 14 (9), 1925–1931.CrossRefGoogle Scholar
Koch, D. L. 1990 Kinetic theory for a monodisperse gas–solid suspension. Phys. Fluids 2 (10), 1711–1723.CrossRefGoogle Scholar
Kraichnan, R. H. 1961 Dynamics of nonlinear stochastic systems. J. Math. Phys. 2, 124–148.CrossRefGoogle Scholar
Kraichnan, R. H. 1965 Lagrangian-history closure approximation for turbulence. Phys. Fluids 8 (4), 575–598.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Minier, J.-P. & Peirano, E. 2001 The pdf approach to turbulent polydispersed two-phase flows. Phys. Rep. 352, 1–214.Google Scholar
Mori, H. 1973a Kinetic equations for the particle density in $\mu $ space. Prog. Theor. Phys. 49, 357–358.Google Scholar
Mori, H. 1973b Statistical-mechanical theory of kinetic equations. Prog. Theor. Phys. 49, 1516–1545.Google Scholar
Onuki, A. 1978 On fluctuations in $\mu $ space. J. Statist. Phys. 18 (5), 475–499.Google Scholar
Pan, L. & Padaon, P. 2010 Relative velocity of inertial particles in turbulent flows. J. Fluid Mech. 661, 73–107.Google Scholar
Pan, L., Padoan, P., Scalo, J., Kritsuk, A. G. & Norman, M. L. 2011 Turbulent clustering of protoplanetary dust and planetesimal formation. Astrophys. J. 740, 1–21.CrossRefGoogle Scholar
Pandya, R. V. R. & Mashayek, F. 2003 Non-isothermal dispersed phase of particles in turbulent flow. J. Fluid Mech. 475, 205–245.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pozorski, J. & Minier, J.-P. 1999 Probability density function modeling of dispersed two-phase turbulent flows. Phys. Rev. E 59, 855–863.CrossRefGoogle Scholar
Rani, S. L. & Balachandar, S. 2003 Evaluation of the equilibrium Eulerian approach for the evolution of particle concentration in isotropic turbulence. Intl J. Multiphase Flow 29, 1793–1816.Google Scholar
Ray, B. & Collins, L. R. 2011 Preferential concentration and relative velocity statistics of inertial particles in Navier–Stokes turbulence with and without filtering. J. Fluid Mech. 680, 488–510.CrossRefGoogle Scholar
Reade, W. C. & Collins, L. R. 2000 Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12 (10), 2530–2540.Google Scholar
Reeks, M. W. 1980 Eulerian direct interaction applied to the statistical motion of particles in a turbulent flow. J. Fluid Mech. 97, 569–590.CrossRefGoogle Scholar
Reeks, M. W. 1991 On a kinetic equation for the transport of particles in turbulent flows. Phys. Fluids A 3 (3), 446–456.Google Scholar
Reeks, M. W. 1992 On the continuum equations for dispersed particles in nonuniform flows. Phys. Fluids A 4, 1290–1303.Google Scholar
Reeks, M. W. 2005 On probability density function equations for particle dispersion in a uniform shear flow. J. Fluid Mech. 522, 263–302.Google Scholar
Shotorban, B. 2011 Preliminary assessment of two-fluid model for direct numerical simulation of particle-laden flows. AIAA J. 49, 438–443.Google Scholar
Simonin, O., Deutsch, E. & Minier, J.-P. 1993 Eulerian prediction of the fluid/particle correlation motion in turbulent two-phase flows. Appl. Sci. Res. 51, 275–283.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3, 1169–1178.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Swailes, D. C. & Darbyshire, K. F. F. 1997 A generalized Fokker–Planck equation for particle transport in random media. Physica A 242, 38–48.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 2000 Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2003 Pair dispersion and preferential concentration of particles in isotropic turbulence. Phys. Fluids 15, 1776–1787.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2007 Refinement of the probability density function model for preferential concentration of aerosol particles in isotropic turbulence. Phys. Fluids 19, 113308.CrossRefGoogle Scholar
Zaichik, L. I., Simonin, O. & Alipchenkov, V. M. 2003 Two statistical models for predicting collision rates of inertial particles in homogeneous isotropic turbulence. Phys. Fluids 15, 2995–3005.Google Scholar
Zaichik, L. I., Simonin, O. & Alipchenkov, V. M. 2006 Collision rates of bidisperse inertial particles in isotropic turbulence. Phys. Fluids 18, 1–13.Google Scholar