Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T07:40:23.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Streaky dynamo equilibria persisting at infinite Reynolds numbers

Published online by Cambridge University Press:  17 December 2019

Kengo Deguchi Open the ORCID record for Kengo Deguchi [Opens in a new window]
Kengo Deguchi*
Affiliation:
School of Mathematics, Monash University, VIC3800, Australia
*
†Email address for correspondence: kengo.deguchi@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

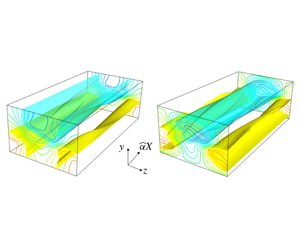
Nonlinear three-dimensional dynamo equilibrium solutions of viscous-resistive magneto-hydrodynamic equations are continued to formally infinite magnetic and hydrodynamic Reynolds numbers. The external driving mechanism of the dynamo is a uniform shear, which constitutes the base laminar flow and cannot support any kinematic dynamo. Nevertheless, an efficient subcritical nonlinear instability mechanism is found to be able to generate large-scale coherent structures known as streaks, for both velocity and magnetic fields. A finite amount of magnetic field generation is identified at the self-consistent asymptotic limit of the nonlinear solutions, thereby confirming the existence of an effective nonlinear dynamo action at astronomically large Reynolds numbers.

JFM classification

Aerodynamics: High-speed flow MHD and Electrohydrodynamics: Dynamo theory Nonlinear Dynamical Systems: Bifurcation
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , R3
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Charbonneau, P. 2014 Solar dynamo theory. Annu. Rev. Astron. Astrophys. 94, 39–48.Google Scholar
Childress, S. & Gilbert, A. D. 1995 Stretch, Twist, Fold: The Fast Dynamo. Springer.Google Scholar
Clever, R. M. & Busse, F. H. 1992 Three-dimensional convection in a horizontal fluid layer subjected to a constant shear. J. Fluid Mech. 234, 511–527.CrossRefGoogle Scholar
Collins, C., Clark, M., Cooper, C. M., Flanagan, K., Khalzov, I. V., Nornberg, M. D., Seidlitz, B., Wallace, J. & Forest, C. B. 2014 Taylor–Couette flow of unmagnetized plasma. Phys. Plasmas 21, 42–117.CrossRefGoogle Scholar
Cowling, T. G. 1934 The magnetic fields of sunspots. Mon. Not. R. Astron. Soc. 94, 39–48.CrossRefGoogle Scholar
Deguchi, K. 2019a High-speed shear-driven dynamos. Part 1. Asymptotic analysis. J. Fluid Mech. 868, 176–211.CrossRefGoogle Scholar
Deguchi, K. 2019b High-speed shear-driven dynamos. Part 2. Numerical analysis. J. Fluid Mech. 876, 830–858.CrossRefGoogle Scholar
Deguchi, K., Hall, P. & Walton, A. G. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.CrossRefGoogle Scholar
Dempsey, L. J., Deguchi, K., Hall, P. & Walton, A. G. 2016 Localized vortex/Tollmien–Schlichting wave interaction states in plane Poiseuille flow. J. Fluid Mech. 791, 97–121.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Fletcher, C. A. J. 1988 Computational Techniques for Fluid Dynamics. Springer.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.CrossRefGoogle Scholar
Guervilly, C. & Cardin, P. 2010 Numerical simulations of dynamos generated in spherical Couette flows. Geophys. Astrophys. Fluid Dyn. 104, 221–248.CrossRefGoogle Scholar
Guseva, A., Hollerbach, R., Willis, A. P. & Avila, M. 2017 Dynamo action in a quasi-Keplerian Taylor–Couette flow. Phys. Rev. Lett. 119, 164501.CrossRefGoogle Scholar
Hall, P. 1988 The nonlinear development of Görtler vortices in growing boundary layers. J. Fluid Mech. 193, 243–266.CrossRefGoogle Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Herault, J., Rincon, F., Cossu, C., Lesur, G., Ogilvie, G. I. & Longaretti, P.-Y. 2011 Periodic magneto rotational dynamo action as a prototype of nonlinear magnetic field generation in shear flows. Phys. Rev. E 84, 036321.Google Scholar
Hof, B., van Doorne, C. W., Westerweel, J., Nieuwstadt, F. T., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.CrossRefGoogle ScholarPubMed
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.CrossRefGoogle Scholar
Kemp, N.1951 The laminar three-dimensional boundary layer and a study of the flow past a side edge. M.Ac.S Thesis, Cornell University, Ithaca, NY.Google Scholar
Larmor, J. 1919 How could a rotating body such as the sun become a magnet. Rep. Brit. Assoc. Adv. Sci. 87, 159–160.Google Scholar
Monchaux, R., Berhanu, M., Bourgoin, M., Moulin, M., Odier, Ph., Pinton, J.-F., Volk, R., Fauve, S., Mordant, N., Pétrélis, F. et al. 2007 Generation of a magnetic field by dynamo action in a turbulent flow of liquid sodium. Phys. Rev. Lett. 98, 044502.CrossRefGoogle Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Nauman, F. & Blackman, E. G. 2017 Sustained turbulence and magnetic energy in nonrotating shear flows. Phys. Rev. E 95, 033202.Google ScholarPubMed
Okamoto, T. J., Antolin, P., De Pontieu, B., Uitenbroek, H., van Doorsselaere, T. & Yokoyama, T. 2015 Resonant absorption of transverse oscillations and associated heating in a solar prominence. Part I. Observational aspects. Astrophys. J. 809 (71), 1–12.CrossRefGoogle Scholar
Ossendrijver, M. 2003 The solar dynamo. Astron. Astrophys. Rev. 11, 287–367.CrossRefGoogle Scholar
Rincon, F. 2019 Dynamo theories. J. Plasma Phys. 85, 205850401.CrossRefGoogle Scholar
Rincon, F., Ogilvie, G. I. & Proctor, M. R. E. 2007 Self-sustaining nonlinear dynamo process in Keplerian shear flows. Phys. Rev. Lett. 98, 254502.CrossRefGoogle ScholarPubMed
Riols, A., Rincon, F., Cossu, C., Lesur, G., Longaretti, P.-Y., Ogilvie, G. I. & Herault, J. 2013 Global bifurcations to subcritical magnetorotational dynamo action in Keplerian shear flow. J. Fluid Mech. 731, 1–45.CrossRefGoogle Scholar
Roberts, P. H. 1964 The stability of hydromagnetic Couette flow. Proc. Camb. Phil. Soc. 60, 635–651.CrossRefGoogle Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Applics 7, 137–146.CrossRefGoogle Scholar
Rubin, S. G. & Tannehill, J. C. 1992 Parabolized/reduced Navier–Stokes computational techniques. Annu. Rev. Fluid Mech. 24, 117–144.CrossRefGoogle Scholar
Squire, H. B. 1933 On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. R. Soc. Lond. A 142 (847), 621–628.CrossRefGoogle Scholar
Tobias, S. M. & Cattaneo, F. 2013 Shear-driven dynamo waves at high magnetic Reynolds number. Nature 497, 463–465.CrossRefGoogle ScholarPubMed
Teed, R. J. & Proctor, M. R. E. 2017 Quasi-cyclic behaviour in non-linear simulations of the shear dynamo. Mon. Not. R. Astron. Soc. 467, 4858–4864.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
Willis, A. P. & Barenghi, C. F. 2002 A Taylor-Couette dynamo. Astron. Astrophys. 393, 339–343.CrossRefGoogle Scholar
Willis, A. P., Cvitanovic, P. & Avila, M. 2013 Revealing the state space of turbulent pipe flow by symmetry reduction. J. Fluid Mech. 721, 514–540.CrossRefGoogle Scholar
Yousef, T. A., Heinemann, T., Schekochihin, A. A., Kleeorin, N., Rogachevskii, I, Iskakov, A. B., Cowley, S. C. & McWilliams, J. C. 2008a Generation of magnetic field by combined action of turbulence and shear. Phys. Rev. Lett. 100, 184501.CrossRefGoogle Scholar
Yousef, T. A., Heinemann, T., Rincon, F., Schekochihin, A. A., Kleeorin, N., Rogachevskii, I, Cowley, S. C. & McWilliams, J. C. 2008b Numerical experiments on dynamo action in sheared and rotating turbulence. Astron. Nachr. 329 (7), 737–749.CrossRefGoogle Scholar
Zel’dovich, Y. B. 1957 The magnetic field in the two-dimensional motion of a conducting turbulent fluid. Sov. Phys. JETP 4, 460–462.Google Scholar