Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T20:30:00.225Z Has data issue: false hasContentIssue false
  • English
  • Français

Supersaturation fluctuations in moist turbulent Rayleigh–Bénard convection: a two-scalar transport problem

Published online by Cambridge University Press:  09 December 2019

Kamal Kant Chandrakar Open the ORCID record for Kamal Kant Chandrakar [Opens in a new window] ,
Will Cantrell ,
Steven Krueger ,
Raymond A. Shaw Open the ORCID record for Raymond A. Shaw [Opens in a new window]  and
Scott Wunsch Open the ORCID record for Scott Wunsch [Opens in a new window]
Kamal Kant Chandrakar*
Affiliation:
Department of Physics, Michigan Technological University, Houghton, MI49931, USA
Will Cantrell
Affiliation:
Department of Physics, Michigan Technological University, Houghton, MI49931, USA
Steven Krueger
Affiliation:
Department of Atmospheric Sciences, University of Utah, Salt Lake City, UT84112, USA
Raymond A. Shaw*
Affiliation:
Department of Physics, Michigan Technological University, Houghton, MI49931, USA
Scott Wunsch
Affiliation:
Applied Physics Laboratory, Johns Hopkins University, Baltimore, MD20723, USA
*
†Email addresses for correspondence: kkchandr@mtu.edu, rashaw@mtu.edu
†Email addresses for correspondence: kkchandr@mtu.edu, rashaw@mtu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Moist Rayleigh–Bénard convection with water saturated boundaries is explored using a One-Dimensional Turbulence model. The system involves both temperature $T$ and water vapour pressure $e_{v}$ as driving scalars. The emphasis of the work is on a supersaturation $s$, a nonlinear combination of $T$ and $e_{v}$ that is crucial to cloud formation. Its mean as well as fluctuation statistics determine cloud droplet growth and therefore precipitation formation and cloud optical properties. To explore the role of relative scalar diffusivities for temperature ($D_{t}$) and water vapour ($D_{v}$), three different regimes are considered: $D_{v}>D_{t}$, $D_{v}\approx D_{t}$ and $D_{v}<D_{t}$. 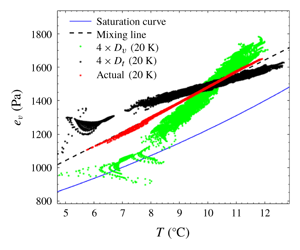Scalar fluxes (Nusselt number, $Nu$ and Sherwood number, $Sh$) and their scalings with moist Rayleigh number $Ra_{moist}$ are consistent with previous studies of one-component convection. Moreover, variances of the scalars in the bulk region increase with their diffusivities and also reasonably follow derived scaling expressions. Eulerian properties plotted in $(T,e_{v})$ coordinates have a different slope compared to an idealized mixing process. Additionally, the scalars are highly correlated, even in the cases of high relative diffusivities (factor of four) $D_{v}$ and $D_{t}$. Based on the above fact and the scaling relation of the scalars, the supersaturation variance is found to vary approximately as $Ra_{moist}^{5/3}$, in agreement with numerical results. Finally, the supersaturation profile in the boundary layer is explored and compares well with scalar boundary layer models. A sharp peak appears in the boundary-layer-supersaturation profile, not only in the variance but also in the mean profile, due to relative diffusivities of the scalars.

JFM classification

Convection: Moist convection Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A19
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109 (11), 114501.CrossRefGoogle ScholarPubMed
Bejan, A. 2013 Convection Heat Transfer. John Wiley & Sons.CrossRefGoogle Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70 (26), 4067–4070.CrossRefGoogle ScholarPubMed
Bogenschutz, P. A. & Krueger, S. K. 2013 A simplified pdf parameterization of subgrid-scale clouds and turbulence for cloud-resolving models. J. Adv. Model. Earth Syst. 5 (2), 195–211.CrossRefGoogle Scholar
Bohren, C. F. & Albrecht, B. A. 1998 Atmospheric Thermodynamics. Oxford University Press.Google Scholar
Bretherton, C. S. 1987 A theory for nonprecipitating moist convection between two parallel plates. Part I. Thermodynamics and linear solutions. J. Atmos. Sci. 44 (14), 1809–1827.2.0.CO;2>CrossRefGoogle Scholar
Bretherton, C. S. 1988 A theory for nonprecipitating convection between two parallel plates. Part II. Nonlinear theory and cloud field organization. J. Atmos. Sci. 45 (17), 2391–2415.2.0.CO;2>CrossRefGoogle Scholar
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69 (2), 026302.CrossRefGoogle ScholarPubMed
Brown, R. A. 1980 Longitudinal instabilities and secondary flows in the planetary boundary layer: a review. Rev. Geophys. 18 (3), 683–697.CrossRefGoogle Scholar
Burns, P. & Meiburg, E. 2012 Sediment-laden fresh water above salt water: linear stability analysis. J. Fluid Mech. 691, 279–314.CrossRefGoogle Scholar
Burrows, A., Marley, M., Hubbard, W. B., Lunine, J. I., Guillot, T., Saumon, D., Freedman, R., Sudarsky, D. & Sharp, C. 1997 A nongray theory of extrasolar giant planets and brown dwarfs. Astrophys. J. 491 (2), 856–875.CrossRefGoogle Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Chandrakar, K. K., Cantrell, W., Chang, K., Ciochetto, D., Niedermeier, D., Ovchinnikov, M., Shaw, R. A. & Yang, F. 2016 Aerosol indirect effect from turbulence-induced broadening of cloud-droplet size distributions. Proc. Natl Acad. Sci. USA 113 (50), 14243–14248.CrossRefGoogle ScholarPubMed
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 58.Google ScholarPubMed
Deardorff, J. W. 1970 Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J. Atmos. Sci. 27 (8), 1211–1213.2.0.CO;2>CrossRefGoogle Scholar
Du Puits, R., Resagk, C., Tilgner, A., Busse, F. H. & Thess, A. 2007 Structure of thermal boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 572, 231–254.CrossRefGoogle Scholar
Echekki, T., Kerstein, A. R., Dreeben, T. D. & Chen, J.-Y. 2001 One-dimensional turbulence simulation of turbulent jet diffusion flames: model formulation and illustrative applications. Combust. Flame 125 (3), 1083–1105.CrossRefGoogle Scholar
Emanuel, K. A. 1994 Atmospheric Convection. Oxford University Press on Demand.Google Scholar
Fleischer, A. S. & Goldstein, R. J. 2002 High-Rayleigh-number convection of pressurized gases in a horizontal enclosure. J. Fluid Mech. 469, 1–12.CrossRefGoogle Scholar
Golaz, J.-C., Larson, V. E. & Cotton, W. R. 2002a A PDF-based model for boundary layer clouds. Part I. Method and model description. J. Atmos. Sci. 59 (24), 3540–3551.2.0.CO;2>CrossRefGoogle Scholar
Golaz, J.-C., Larson, V. E. & Cotton, W. R. 2002b A PDF-based model for boundary layer clouds. Part II. Model results. J. Atmos. Sci. 59 (24), 3552–3571.2.0.CO;2>CrossRefGoogle Scholar
Gonzalez-Juez, E., Kerstein, A. R. & Lignell, D. O. 2011 Fluxes across double-diffusive interfaces: a one-dimensional-turbulence study. J. Fluid Mech. 677, 218–254.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16 (12), 4462–4472.CrossRefGoogle Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17 (3), 405–432.CrossRefGoogle Scholar
Howard, L. N. 1966 Convection at high Rayleigh number. In Applied Mechanics, pp. 1109–1115. Springer.CrossRefGoogle Scholar
Huppert, H. E. & Turner, J. S. 1981 Double-diffusive convection. J. Fluid Mech. 106, 299–329.CrossRefGoogle Scholar
Kelley, D. E., Fernando, H. J. S., Gargett, A. E., Tanny, J. & Özsoy, E. 2003 The diffusive regime of double-diffusive convection. Prog. Oceanogr. 56 (3–4), 461–481.CrossRefGoogle Scholar
Kerstein, A. R. 1999 One-dimensional turbulence: model formulation and application to homogeneous turbulence, shear flows, and buoyant stratified flows. J. Fluid Mech. 392, 277–334.CrossRefGoogle Scholar
Kreidberg, L., Bean, J. L., Désert, J.-M., Benneke, B., Deming, D., Stevenson, K. B., Seager, S., Berta-Thompson, Z., Seifahrt, A. & Homeier, D. 2014 Clouds in the atmosphere of the super-earth exoplanet GJ 1214b. Nature 505 (7481), 69–72.CrossRefGoogle ScholarPubMed
Krueger, S. K. 1993 Linear eddy modeling of entrainment and mixing in stratus clouds. J. Atmos. Sci. 50 (18), 3078–3090.2.0.CO;2>CrossRefGoogle Scholar
Krueger, S. K., Su, C.-W. & McMurtry, P. A. 1997 Modeling entrainment and finescale mixing in cumulus clouds. J. Atmos. Sci. 54 (23), 2697–2712.2.0.CO;2>CrossRefGoogle Scholar
Kulmala, M., Rannik, Ü., Zapadinsky, E. L. & Clement, C. F. 1997 The effect of saturation fluctuations on droplet growth. J. Aero. Sci. 28 (8), 1395–1409.CrossRefGoogle Scholar
Lamb, D. & Shaw, R. A. 2016 Visualizing vapor pressure: a mechanical demonstration of liquid–vapor phase equilibrium. Bull. Am. Meteorol. Soc. 97 (8), 1355–1362.CrossRefGoogle Scholar
Lilly, D. K. 1968 Models of cloud-topped mixed layers under a strong inversion. Q. J. R. Meteorol. Soc. 94 (401), 292–309.CrossRefGoogle Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225 (1161), 196–212.Google Scholar
Marley, M. S., Ackerman, A. S., Cuzzi, J. N. & Kitzmann, D. 2013 Clouds and hazes in exoplanet atmospheres. Compar. Climatol. Terr. Planets 1, 367–391.Google Scholar
Mellado, J. P. 2017 Cloud-top entrainment in stratocumulus clouds. Annu. Rev. Fluid Mech. 49, 145–169.CrossRefGoogle Scholar
Mellado, J. P., Puche, M. & van Heerwaarden, C. C. 2017 Moisture statistics in free convective boundary layers growing into linearly stratified atmospheres. Q. J. R. Meteorol. Soc. 143 (707), 2403–2419.CrossRefGoogle Scholar
Mellor, G. L. 1977 The Gaussian cloud model relations. J. Atmos. Sci. 34 (2), 356–358.2.0.CO;2>CrossRefGoogle Scholar
Moeng, C.-H. & Rotunno, R. 1990 Vertical-velocity skewness in the buoyancy-driven boundary layer. J. Atmos. Sci. 47 (9), 1149–1162.2.0.CO;2>CrossRefGoogle Scholar
Niedermeier, D., Chang, K., Cantrell, W., Chandrakar, K. K., Ciochetto, D. & Shaw, R. A. 2018 Observation of a link between energy dissipation rate and oscillation frequency of the large-scale circulation in dry and moist Rayleigh–Bénard turbulence. Phys. Rev. Fluids 3 (8), 083501.CrossRefGoogle Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404 (6780), 837.CrossRefGoogle ScholarPubMed
Niemela, J. J. & Sreenivasan, K. R. 2006 Turbulent convection at high Rayleigh numbers and aspect ratio 4. J. Fluid Mech. 557, 411–422.CrossRefGoogle Scholar
Pauluis, O. & Schumacher, J. 2011 Self-aggregation of clouds in conditionally unstable moist convection. Proc. Natl Acad. Sci. USA 108 (31), 12623–12628.CrossRefGoogle ScholarPubMed
Pauluis, O. & Schumacher, J. 2010 Idealized moist Rayleigh–Bénard convection with piecewise linear equation of state. Commun. Math. Sci. 8 (1), 295–319.CrossRefGoogle Scholar
Politovich, M. K. & Cooper, W. A. 1988 Variability of the supersaturation in cumulus clouds. J. Atmos. Sci. 45 (11), 1651–1664.2.0.CO;2>CrossRefGoogle Scholar
Randall, D. A. 1987 Turbulent fluxes of liquid water and buoyancy in partly cloudy layers. J. Atmos. Sci. 44 (5), 850–858.2.0.CO;2>CrossRefGoogle Scholar
Schlichting, H., Gersten, K., Krause, E., Oertel, H. & Mayes, K. 1955 Boundary-Layer Theory, vol. 7. Springer.Google Scholar
Schmitt, R. W. 1994 Double diffusion in oceanography. Annu. Rev. Fluid Mech. 26 (1), 255–285.CrossRefGoogle Scholar
Siebert, H. & Shaw, R. A. 2017 Supersaturation fluctuations during the early stage of cumulus formation. J. Atmos. Sci. 74 (4), 975–988.CrossRefGoogle Scholar
Sommeria, G. & Deardorff, J. W. 1977 Subgrid-scale condensation in models of nonprecipitating clouds. J. Atmos. Sci. 34 (2), 344–355.2.0.CO;2>CrossRefGoogle Scholar
Sorbjan, Z. 1989 Structure of the Atmospheric Boundary Layer. Prentice Hall.Google Scholar
Stechmann, S. N. 2014 Multiscale eddy simulation for moist atmospheric convection: preliminary investigation. J. Comput. Phys. 271, 99–117.CrossRefGoogle Scholar
Stevens, B. 2005 Atmospheric moist convection. Annu. Rev. Earth Planet. Sci. 33, 605–643.CrossRefGoogle Scholar
Stratmann, F., Kiselev, A., Wurzler, S., Wendisch, M., Heintzenberg, J., Charlson, R. J., Diehl, K., Wex, H. & Schmidt, S. 2004 Laboratory studies and numerical simulations of cloud droplet formation under realistic supersaturation conditions. J. Atmos. Ocean. Technol. 21 (6), 876–887.2.0.CO;2>CrossRefGoogle Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47 (4), R2253.CrossRefGoogle ScholarPubMed
Townsend, A. A. 1959 Temperature fluctuations over a heated horizontal surface. J. Fluid Mech. 5 (2), 209–241.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.CrossRefGoogle Scholar
Wunsch, S. & Kerstein, A. 2001 A model for layer formation in stably stratified turbulence. Phys. Fluids 13 (3), 702–712.CrossRefGoogle Scholar
Wunsch, S. & Kerstein, A. R. 2005 A stochastic model for high-Rayleigh-number convection. J. Fluid Mech. 528, 173–205.CrossRefGoogle Scholar
Wyngaard, J. C., Pennell, W. T., Lenschow, D. H. & LeMone, M. A. 1978 The temperature-humidity covariance budget in the convective boundary layer. J. Atmos. Sci. 35 (1), 47–58.2.0.CO;2>CrossRefGoogle Scholar
Wyngaard, J. C. 1992 Atmospheric turbulence. Annu. Rev. Fluid Mech. 24 (1), 205–234.CrossRefGoogle Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88 (6), 064501.CrossRefGoogle ScholarPubMed
Zaussinger, F. & Spruit, H. C. 2013 Semiconvection: numerical simulations. Astron. Astrophys. 554, A119.CrossRefGoogle Scholar
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104 (10), 104301.CrossRefGoogle ScholarPubMed