Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T22:09:42.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Tandem cavity collapse in a high-speed droplet impinging on a 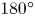$180^{\circ }$ constrained wall

Published online by Cambridge University Press:  15 December 2021

Wangxia Wu Open the ORCID record for Wangxia Wu [Opens in a new window] ,
Bing Wang Open the ORCID record for Bing Wang [Opens in a new window]  and
Qingquan Liu Open the ORCID record for Qingquan Liu [Opens in a new window]
Wangxia Wu
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, PR China
Bing Wang
Affiliation:
School of Aerospace Engineering, Tsinghua University, Beijing 100084, PR China
Qingquan Liu*
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, PR China
*
†Email address for correspondence: liuqq@bit.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A focusing shock wave can be generated during the high-speed impact of a droplet on a $180^\circ$ constrained wall, which can be used to realise energy convergence on a small scale. In this study, to realise high energy convergence and peak pressure amplification, a configuration of droplets embedded with cavities is proposed for high-speed impingement on a $180^\circ$ constrained wall. A multicomponent two-phase compressible flow model considering the phase transition is used to simulate the high-speed droplet impingement process. The properties of the embedded cavities can influence the collapse pressure peak. The collapse of an embedded single air cavity or vapour cavity, as well as the cavities in a tandem array, is simulated in this study. The physical evolution mechanisms of the impinging droplet and the embedded cavities are investigated qualitatively and quantitatively by characterising the focusing shock wave generated inside the droplet and its interaction with different cavity configurations. The interaction dynamics between the cavities is analysed and a theoretical prediction model for the intensity of each cavity collapse in the tandem array is established. With the help of this theoretical model, the influencing factors for the collapse intensities of the tandem cavities are identified. The results reveal that the properties of the initial shock wave and the interval between the cavities are two predominant factors for the amplification of the collapse intensity. This study enhances the understanding of the physical process of shock-induced tandem-cavity collapse.

JFM classification

Compressible Flows: Shock waves Drops and Bubbles: Drops Drops and Bubbles: Bubble dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 932 , 10 February 2022 , A52
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Allaire, G., Clerc, S. & Kokh, S. 2002 A five-equation model for the simulation of interfaces between compressible fluids. J. Comput. Phys. 181 (2), 577–616.CrossRefGoogle Scholar
Apazidis, N. 2016 Numerical investigation of shock induced bubble collapse in water. Phys. Fluids 28 (4), 225–240.CrossRefGoogle Scholar
Apazidis, N. & Lesser, M.B. 1996 On generation and convergence of polygonal-shaped shock waves. J. Fluid Mech. 309 (-1), 301–319.CrossRefGoogle Scholar
Bagabir, A. & Drikakis, D. 2001 Mach number effects on shock-bubble interaction. Shock Waves 11 (3), 209–218.CrossRefGoogle Scholar
Ball, G.J., Howell, B.P., Leighton, T.G. & Schofield, M.J. 2000 Shock-induced collapse of a cylindrical air cavity in water: a free-Lagrange simulation. Shock Waves 10 (4), 265–276.CrossRefGoogle Scholar
Bempedelis, N. & Ventikos, Y. 2020 Energy focusing in shock-collapsed bubble arrays. J. Fluid Mech. 900, A44.CrossRefGoogle Scholar
Betney, M.R., Tully, B., Hawker, N.A. & Ventikos, Y. 2015 Computational modelling of the interaction of shock waves with multiple gas-filled bubbles in a liquid. Phys. Fluids 27 (3), 94–98.CrossRefGoogle Scholar
Bourne, N.K. & Field, J.E. 1992 Shock-induced collapse of single cavities in liquids. J. Fluid Mech. 244 (1), 225–240.CrossRefGoogle Scholar
Bourne, N.K. & Field, J.E. 1999 Shock-induced collapse and luminescence by cavities. Phil. Trans. R. Soc. Lond. A 357, 295–311.CrossRefGoogle Scholar
Bremond, N., Arora, M., Ohl, C.D. & Lohse, D. 2006 Controlled multibubble surface cavitation. Phys. Rev. Lett. 96 (22), 224501–224501.CrossRefGoogle ScholarPubMed
Brennen, C.E. 1995 Cavitation and Bubble Dynamics. Oxford University Press.Google Scholar
Brujan, E.A., Ikeda, T. & Matsumoto, Y. 2012 Shock wave emission from a cloud of bubbles. Soft Matt. 8 (21), 5777–5783.CrossRefGoogle Scholar
Bui, T.T., Ong, E.T., Khoo, B.C., Klaseboer, E. & Hung, K.C. 2006 A fast algorithm for modeling multiple bubbles dynamics. J. Comput. Phys. 216 (2), 430–453.CrossRefGoogle Scholar
Chahine, G.L. & Duraiswami, R. 1992 Dynamical interactions in a multi-bubble cloud. Trans. ASME J. Fluids Engng 114 (4), 680–686.CrossRefGoogle Scholar
Cui, P., Zhang, A.M., Wang, S.P. & Liu, Y.L. 2020 Experimental study on interaction, shock wave emission and ice breaking of two collapsing bubbles. J. Fluid Mech. 897, A25.CrossRefGoogle Scholar
Dear, J.P. & Field, J.E. 1988 A study of the collapse of arrays of cavities. J. Fluid Mech. 190, 409–425.CrossRefGoogle Scholar
Dear, J.P., Field, J.E. & Walton, A.J. 1988 Gas compression and jet formation in cavities collapsed by a shock wave. Nature 332 (6164), 505–508.CrossRefGoogle Scholar
Ding, Z. & Gracewski, S.M. 1996 The behaviour of a gas cavity impacted by a weak or strong shock wave. J. Fluid Mech. 309, 183–209.CrossRefGoogle Scholar
Felix, D., Stefan, H. & Nikolaus, A.A. 2016 Shock mach number influence on reaction wave types and mixing in reactive shock-bubble interaction. Combust. Flame 174, 85–99.Google Scholar
Field, J.E., Dear, J.P. & Ogren, J.E. 1989 The effects of target compliance on liquid drop impact. J. Appl. Phys. 65 (2), 533–540.CrossRefGoogle Scholar
Field, J.E., Lesser, M.B. & Dear, J.P. 1985 Studies of two-dimensional liquid-wedge impact and their relevance to liquid-drop impact problems. Proc. R. Soc. Lond. A 401, 225–249.Google Scholar
Fuster, D. 2019 A review of models for bubble clusters in cavitating flows. Flow Turbul. Combust. 102, 497–536.CrossRefGoogle Scholar
Fuster, D., Conoir, J.M. & Colonius, T. 2014 Effect of direct bubble-bubble interactions on linear-wave propagation in bubbly liquids. Phys. Rev. E 90, 063010.CrossRefGoogle ScholarPubMed
Gottlieb, S. & Shu, C.W. 1998 Total variation diminishing Runge–Kutta schemes. Math. Comput. 67 (221), 73–85.CrossRefGoogle Scholar
Han, E., Hantke, M. & Müller, S. 2017 Efficient and robust relaxation procedures for multi-component mixtures including phase transition. J. Comput. Phys. 338, 217–239.CrossRefGoogle Scholar
Hansson, I., Kedrinskii, V. & Morch, K.A. 1982 On the dynamics of cavity clusters. J. Phys. D: Appl. Phys. 15 (9), 1725–1734.CrossRefGoogle Scholar
Hawker, N.A. & Ventikos, Y. 2012 Interaction of a strong shockwave with a gas bubble in a liquid medium: a numerical study. J. Fluid Mech. 701, 59–97.CrossRefGoogle Scholar
Heymann, F.J. 1969 High-speed impact between a liquid drop and a solid surface. J. Appl. Phys. 40 (13), 5113–5122.CrossRefGoogle Scholar
Hilgenfeldt, S., Brenner, M.P., Grossmann, S. & Lohse, D. 1998 Analysis of Rayleigh–Plesset dynamics for sonoluminescing bubbles. J. Fluid Mech. 365 (365), 171–204.CrossRefGoogle Scholar
Huang, Y.C. 1973 Note on shock-wave velocity in high-speed liquid-solid impact. J. Appl. Phys. 44 (4), 1868.CrossRefGoogle Scholar
Hung, C.F. & Hwangfu, J.J. 2010 Experimental study of the behaviour of mini-charge underwater explosion bubbles near different boundaries. J. Fluid Mech. 651, 55–80.CrossRefGoogle Scholar
Jeong, S.H., Greif, R. & Russo, R.E. 1998 Propagation of the shock wave generated from excimer laser heating of aluminum targets in comparison with ideal blast wave theory. Appl. Surf. Sci. 127–129, 1029–1034.CrossRefGoogle Scholar
Johnsen, E. & Colonius, T. 2006 Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 219 (2), 715–732.CrossRefGoogle Scholar
Johnsen, E. & Colonius, T. 2009 Numerical simulations of non-spherical bubble collapse. J. Fluid Mech. 629 (629), 231–262.CrossRefGoogle ScholarPubMed
Jones, J.G. 1963 Shock-expansion theory and simple wave perturbation. J. Fluid Mech. 17 (4), 506–512.CrossRefGoogle Scholar
Keller, J.B. 1954 Geometrical acoustics. I. The theory of weak shock waves. J. Appl. Phys. 25 (8), 938–947.CrossRefGoogle Scholar
Kiyama, A., Endo, N., Kawamoto, S., Katsuta, C., Oida, K., Tanaka, A. & Tagawa, Y. 2019 Visualization of penetration of a high-speed focused microjet into gel and animal skin. J. Vis. (Visualization) 22 (3), 449–457.CrossRefGoogle Scholar
Klaseboer, E., Fong, S.W., Turangan, C.K., Khoo, B.C., Szeri, A.J., Calvisi, M.L., Sankin, G.N. & Zhong, P. 2007 Interaction of lithotripter shockwaves with single inertial cavitation bubbles. J. Fluid Mech. 593, 33–56.CrossRefGoogle ScholarPubMed
Klaseboer, E., Turangan, C., Fong, S.W., Liu, T.G., Hung, K.C. & Khoo, B.C. 2006 Simulations of pressure pulse-bubble interaction using boundary element method. Comput. Meth. Appl. Mech. Engng 195 (33–36), 4287–4302.CrossRefGoogle Scholar
Kumar, P. & Saini, R.P. 2010 Study of cavitation in hydro turbines—a review. Renew. Sust. Energ. Rev. 14 (1), 374–383.CrossRefGoogle Scholar
Lapworth, K.C. 1959 An experimental investigation of the stability of plane shock waves. J. Fluid Mech. 6 (3), 469–480.CrossRefGoogle Scholar
Lauer, E., Hu, X.Y., Hickel, S. & Adams, N.A. 2012 Numerical investigation of collapsing cavity arrays. Phys. Fluids 24 (5), 94–12.CrossRefGoogle Scholar
Le Martelot, S., Saurel, R. & Nkonga, B. 2014 Towards the direct numerical simulation of nucleate boiling flows. Intl J. Multiphase Flow 66, 62–78.CrossRefGoogle Scholar
Leppinen, D.M., Wang, Q.X. & Blake, J.R. 2013 Pulsating Bubbles Near Boundaries, pp. 33–65. Springer.Google Scholar
Lesser, M.B. 1981 Analytic solutions of liquid-drop impact problems. Proc. R. Soc. Lond. A 377, 289–308.Google Scholar
Lindl, J. 1998 Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 2 (11), 3933–4024.CrossRefGoogle Scholar
Lokhandwalla, M. & Sturtevant, B. 2001 Mechanical haemolysis in shock wave lithotripsy (SWL): II. In vitro cell lysis due to shear. Phys. Med. Biol. 46 (2), 1245–1264.CrossRefGoogle Scholar
Luo, J. & Niu, Z. 2019 Jet and shock wave from collapse of two cavitation bubbles. Sci. Rep. 9, 1352.CrossRefGoogle ScholarPubMed
Maeda, K. & Colonius, T. 2019 Bubble cloud dynamics in an ultrasound field. J. Fluid Mech. 862, 1105–1134.CrossRefGoogle Scholar
Maxwell, A.D., Wang, T.Y., Cain, C.A., Fowlkes, J.B., Sapozhnikov, O.A., Bailey, M.R. & Xu, Z. 2011 Cavitation clouds created by shock scattering from bubbles during histotripsy. J. Acoust. Soc. Am. 130 (4), 1888–1898.CrossRefGoogle ScholarPubMed
Menikoff, R. & Plohr, B.J. 1989 The Riemann problem for fluid flow of real materials. Rev. Mod. Phys. 61 (1), 75.CrossRefGoogle Scholar
Michael, L. & Nikiforakis, N. 2019 The evolution of the temperature field during cavity collapse in liquid nitromethane. Part I: inert case. Shock Waves 29, 153–172.CrossRefGoogle Scholar
Mitragotri, S. 2005 Healing sound: the use of ultrasound in drug delivery and other therapeutic applications. Nat. Rev. Drug Discov. 4 (3), 255–260.CrossRefGoogle ScholarPubMed
Mittal, R. & Iaccarino, G. 2004 Immersed boundary methods. Annu. Rev. Fluid Mech. 14 (37), 239–261.Google Scholar
Needham, C.E. 2010 Blast Waves. Springer.CrossRefGoogle Scholar
Niederhaus, J.H.J., Greenough, J.A., Oakley, J.G., Ranjan, D., Anderson, M.H. & Bonazza, R. 2008 A computational parameter study for the three-dimensional shock-bubble interaction. J. Fluid Mech. 594, 85–124.CrossRefGoogle Scholar
Ohl, S., Klaseboer, E. & Khoo, B.C. 2015 Bubbles with shock waves and ultrasound: a review. Interface Focus 5, 20150019.CrossRefGoogle ScholarPubMed
Ohl, S.W. & Ohl, C.D. 2013 Shock Wave Interaction with Single Bubbles and Bubble Clouds, pp. 3–31. Springer.Google Scholar
Rasthofer, U., Wermelinger, F., Karnakov, P., Šukys, J. & Koumoutsakos, P. 2019 Computational study of the collapse of a cloud with 12 500 gas bubbles in a liquid. Phys. Rev. Fluids 4 (6), 063602.CrossRefGoogle Scholar
Reisman, G.E., Wang, Y.C. & Brennen, C.E. 1998 Observations of shock waves in cloud cavitation. J. Fluid Mech. 355, 255–283.CrossRefGoogle Scholar
Sankin, G.N., Simmons, W.N., Zhu, S.L. & Zhong, P. 2006 Shock wave interaction with laser-generated single bubbles. Phys. Rev. Lett. 95 (3), 034501.CrossRefGoogle Scholar
Saurel, R., Gavrilyuk, S. & Renaud, F. 2003 A multiphase model with internal degrees of freedom: application to shock–bubble interaction. J. Fluid Mech. 495, 283–321.CrossRefGoogle Scholar
Saurel, R., Petitpas, F. & Abgrall, R. 2008 Modelling phase transition in metastable liquids: application to cavitating and flashing flows. J. Fluid Mech. 607, 313–350.CrossRefGoogle Scholar
Sommerfeld, M. & Müller, H.M. 1988 Experimental and numerical studies of shock wave focusing in water. Exp. Fluids 6 (3), 209–216.CrossRefGoogle Scholar
Sturtevant, B. & Kulkarny, V.A. 1976 The focusing of weak shock waves. J. Fluid Mech. 73 (4), 651–671.CrossRefGoogle Scholar
Swantek, A.B. & Austin, J.M. 2010 Collapse of void arrays under stress wave loading. J. Fluid Mech. 649 (649), 399–427.CrossRefGoogle Scholar
Taleyarkhan, R.P., West, C.D., Cho, J.S., Lahey, R.T., Nigmatulin, R.I. & Block, R.C. 2002 Evidence for nuclear emissions during acoustic cavitation. Science 295 (5562), 1868–1873.CrossRefGoogle ScholarPubMed
Thompson, K.W. 1990 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 89 (2), 439–461.CrossRefGoogle Scholar
Tiwari, A. 2014 Detailed Simulations of Bubble-Cluster Dynamics. University of Illinois at Urbana-Champaign.Google Scholar
Tiwari, A., Freund, J.B. & Pantano, C. 2013 A diffuse interface model with immiscibility preservation. J. Comput. Phys. 252, 290–309.CrossRefGoogle ScholarPubMed
Tiwari, A., Pantano, C. & Freund, J.B. 2015 Growth-and-collapse dynamics of small bubble clusters near a wall. J. Fluid Mech. 775, 1–23.CrossRefGoogle Scholar
Tomita, Y., Shima, A. & Ohno, T. 1984 Collapse of multiple gas bubbles by a shock wave and induced impulsive pressure. J. Appl. Phys. 56 (1), 125–131.CrossRefGoogle Scholar
Tomita, Y., Shima, A. & Takahashi, K. 1983 The collapse of a gas bubble attached to a solid wall by a shock wave and the induced impact pressure. Trans. ASME J. Fluids Engng 105 (3), 341–347.CrossRefGoogle Scholar
Toro, E.F. 2013 Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer.Google Scholar
Tully, B., Hawker, N. & Ventikos, Y. 2016 Modeling asymmetric cavity collapse with plasma equations of state. Phys. Rev. E 93 (5), 053105.CrossRefGoogle ScholarPubMed
Ventikos, Y. & Hawker, N. 2017 High velocity droplet impacts. US Patent 9,704,603.Google Scholar
Wang, B., Xiang, G. & Hu, X.Y. 2018 An incremental-stencil WENO reconstruction for simulation of compressible two-phase flows. Intl J. Multiphase Flow 104, 20–31.CrossRefGoogle Scholar
Wermelinger, F., Hejazialhosseini, B., Hadjidoukas, P., Rossinelli, D. & Koumoutsakos, P. 2016 An efficient compressible multicomponent flow solver for heterogeneous CPU/GPU architectures. pp. 1–10. Association for Computing Machinery.CrossRefGoogle Scholar
Whitham, G.B. 1957 A new approach to problems of shock dynamics part I two-dimensional problems. J. Fluid Mech. 2 (2), 145–171.CrossRefGoogle Scholar
Whitham, G.B. 2006 On the propagation of shock waves through regions of non-uniform area or flow. J. Fluid Mech. 4 (4), 337–360.CrossRefGoogle Scholar
Whitham, G.B. & Fowler, R.G. 1975 Linear and nonlinear waves. Phys. Today 28 (6), xvi+636.CrossRefGoogle Scholar
Wu, W., Liu, Q. & Wang, B. 2021 Curved surface effect on high-speed droplet impingement. J. Fluid Mech. 909, A7.CrossRefGoogle Scholar
Wu, W., Wang, B. & Xiang, G. 2019 Impingement of high-speed cylindrical droplets embedded with an air/vapour cavity on a rigid wall: numerical analysis. J. Fluid Mech. 864, 1058–1087.CrossRefGoogle Scholar
Wu, W., Xiang, G. & Wang, B. 2018 On high-speed impingement of cylindrical droplets upon solid wall considering cavitation effects. J. Fluid Mech. 857, 851–877.CrossRefGoogle Scholar
Xiang, G. & Wang, B. 2017 Numerical study of a planar shock interacting with a cylindrical water column embedded with an air cavity. J. Fluid Mech. 825, 825–852.CrossRefGoogle Scholar
Zein, A., Hantke, M. & Warnecke, G. 2010 Modeling phase transition for compressible two-phase flows applied to metastable liquids. J. Comput. Phys. 229 (8), 2964–2998.CrossRefGoogle Scholar
Zein, A., Hantke, M. & Warnecke, G. 2013 On the modeling and simulation of a laser-induced cavitation bubble. Intl J. Numer. Meth. Fluids 73 (2), 172–203.CrossRefGoogle Scholar