Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T18:04:33.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Transport equation for the isotropic turbulent energy dissipation rate in the far-wake of a circular cylinder

Published online by Cambridge University Press:  30 October 2015

S. L. Tang ,
R. A. Antonia ,
L. Djenidi  and
Y. Zhou
S. L. Tang
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, PR China School of Engineering, University of Newcastle, NSW 2308, Australia
R. A. Antonia*
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
L. Djenidi
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
Y. Zhou
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, PR China
*
†Email address for correspondence: robert.antonia@newcastle.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

The transport equation for the isotropic turbulent energy dissipation rate $\overline{{\it\epsilon}}_{iso}$ along the centreline in the far-wake of a circular cylinder is derived by applying the limit at small separations to the two-point energy budget equation. It is found that the imbalance between the production and the destruction of $\overline{{\it\epsilon}}_{iso}$, respectively due to vortex stretching and viscosity, is governed by both the streamwise advection and the lateral turbulent diffusion (the former contributes more to the budget than the latter). This imbalance differs intrinsically from that in other flows, e.g. grid turbulence and the flow along the centreline of a fully developed channel, where either the streamwise advection or the lateral turbulent diffusion of $\overline{{\it\epsilon}}_{iso}$ governs the imbalance. More importantly, the different types of imbalance represent different constraints on the relation between the skewness of the longitudinal velocity derivative $S$ and the destruction coefficient of enstrophy $G$. This results in a non-universal approach of $S$ towards a constant value as the Taylor microscale Reynolds number $R_{{\it\lambda}}$ increases. For the present flow, the magnitude of $S$ decreases initially ($R_{{\it\lambda}}\leqslant 40$) before increasing ($R_{{\it\lambda}}>40$) towards this constant value. The constancy of $S$ at large 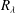$R_{{\it\lambda}}$ violates the modified similarity hypothesis introduced by Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85) but is consistent with the original similarity hypotheses (Kolmogorov, Dokl. Akad. Nauk SSSR, vol. 30, 1941b, pp. 299–303 (see also 1991 Proc. R. Soc. Lond. A, vol. 434, pp. 9–13)) ($K41$), and, more importantly, with the almost completely self-preserving nature of the plane far-wake.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 784 , 10 December 2015 , pp. 109 - 129
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.Google Scholar
Anselmet, F., Gagne, Y., Hopfinger, E. J. & Antonia, R. A. 1984 Higher-order velocity structure functions in turbulent shear flows. J. Fluid Mech. 140, 63–89.CrossRefGoogle Scholar
Antonia, R. A. & Browne, L. W. 1986 Anisotropy of temperature dissipation in a turbulent wake. J. Fluid Mech. 163, 393–403.CrossRefGoogle Scholar
Antonia, R. A., Browne, L. W. B., Bisset, D. K. & Fulachier, L. 1987 A description of the organized motion in the turbulent far wake of a cylinder at low Reynolds number. J. Fluid Mech. 184, 423–444.Google Scholar
Antonia, R. A., Browne, L. W. B. & Shah, D. A. 1988 Characteristics of vorticity fluctuations in a turbulent wake. J. Fluid Mech. 189, 349–365.Google Scholar
Antonia, R. A. & Burattini, P. 2006 Approach to the $4/5$ law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.Google Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipation range on Kolmogorov scales. Phys. Fluids 26, 045105.CrossRefGoogle Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.Google Scholar
Antonia, R. A., Zhou, T., Danaila, L. & Anselmet, F. 2000 Streamwise inhomogeneity of decaying grid turbulence. Phys. Fluids 12, 3086–3089.CrossRefGoogle Scholar
Antonia, R. A., Zhou, T. & Romano, G. P. 2002 Small-scale turbulence characteristics of two-dimensional bluff body wakes. J. Fluid Mech. 459, 67–92.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1947 Decay of vorticity in isotropic turbulence. Proc. R. Soc. Lond. A 190, 534–550.Google Scholar
Belin, F., Maurer, J., Tabeling, P. & Willaime, H. 1997 Velocity gradient distributions in fully developed turbulence: experimental study. Phys. Fluids 9, 3843–3850.Google Scholar
Bisset, D. K., Antonia, R. A. & Britz, D. 1990a Structure of large-scale vorticity in a turbulent far wake. J. Fluid Mech. 218, 463–482.Google Scholar
Bisset, D. K., Antonia, R. A. & Browne, L. W. B. 1990b Spatial organization of large structures in the turbulent far wake of a cylinder. J. Fluid Mech. 218, 439–461.Google Scholar
Brown, G. L. & Roshko, A. 2012 Turbulent shear layers and wakes. J. Turbul. 13, 1–32.CrossRefGoogle Scholar
Browne, L. W., Antonia, R. A. & Shah, D. A. 1987 Turbulent energy dissipation in a wake. J. Fluid Mech. 179, 307–326.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005 Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101.Google Scholar
Camussi, R. & Guj, G. 1995 Experimental analysis of scaling laws in low and moderate $Re$ grid generated turbulence. Exp. Fluids 24, 63–67.Google Scholar
Champagne, F. H. 1978 The fine-scale structure of the turbulent velocity field. J. Fluid Mech. 86, 67–108.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 1999 A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 2001 Turbulent energy scale-budget equations in a fully developed channel flow. J. Fluid Mech. 430, 87–109.Google Scholar
Danaila, L., Antonia, R. A. & Burattini, P. 2004 Progress in studying small-scale turbulence using ‘exact’ two-point equations. New J. Phys. 6, 2–23.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Djenidi, L. & Antonia, R. A. 2012 A spectral chart method for estimating the mean turbulent kinetic energy dissipation rate. Exp. Fluids 53, 1005–1013.Google Scholar
Djenidi, L. & Antonia, R. A. 2014 Transport equation for the mean turbulent energy dissipation rate in low- $R_{{\it\lambda}}$ grid turbulence. J. Fluid Mech. 747, 288–315.CrossRefGoogle Scholar
Frisch, U. 1996 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Frisch, U., Sulem, P. L. & Nelkin, M. 1978 A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87, 719–736.Google Scholar
Fukayama, D., Oyamada, T., Nakano, T., Gotoh, T. & Yamamoto, K. 2000 Longitudinal structure functions in decaying and forced turbulence. J. Phys. Soc. Japan 69, 701–715.CrossRefGoogle Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 1065–1081.Google Scholar
Hao, Z., Zhou, T., Chua, L. P. & Yu, S. C. M. 2008 Approximations to energy and temperature dissipation rates in the far field of a cylinder wake. Exp. Therm. Fluid Sci. 32, 791–799.Google Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Kolmogorov, A. 1941a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19–21 (see also 1991 Proc. R. Soc. Lond. A 434, 15–17).Google Scholar
Kolmogorov, A. N. 1941b Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303 (see also 1991 Proc. R. Soc. Lond. A 434, 9–13).Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Larssen, J. V. & Devenport, W. J. 2011 On the generation of large-scale homogeneous turbulence. Exp. Fluids 50, 1207–1223.Google Scholar
Lee, S. K., Djenidi, L., Antonia, R. A. & Danaila, L. 2013 On the destruction coefficients for slightly heated decaying grid turbulence. Intl J. Heat Fluid Flow 43, 129–136.Google Scholar
Lefeuvre, N., Djenidi, L., Antonia, R. A. & Zhou, T. 2014 Turbulent kinetic energy and temperature variance budgets in the far-wake generated by a circular cylinder. In 19th Australasian Fluid Mechanics Conference, Melbourne, Paper 106.Google Scholar
Mansour, N. N. & Wray, A. A. 1994 Decay of isotropic turbulence at low Reynolds number. Phys. Fluids 6, 808–814.CrossRefGoogle Scholar
Qian, J. 1986 A closure theory of intermittency of turbulence. Phys. Fluids 29, 2165.Google Scholar
Qian, J. 1994 Skewness factor of turbulent velocity derivative. Acta Mechanica Sin. 10, 12–15.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.Google Scholar
Saffman, P. G. 1970 Dependence on Reynolds number of high-order moments of velocity derivatives in isotropic turbulence. Phys. Fluids 13, 2193–2194.Google Scholar
Sreenivasan, K. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Tabeling, P., Zocchi, G., Belin, F., Maurer, J. & Willaime, H. 1996 Probability density functions, skewness, and flatness in large Reynolds number turbulence. Phys. Rev. E 53, 1613–1621.CrossRefGoogle ScholarPubMed
Tang, S. L., Antonia, R. A., Djenidi, L., Abe, H., Zhou, T., Danaila, L. & Zhou, Y. 2015a Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y. 2015b Consequence of self-preservation in a turbulent far-wake. In The 9th Symposium on Turbulence and Shear Flow Phenomena (TSFP-9), June 30th–July 3rd, Melbourne, Australia, Paper 300.Google Scholar
Tavoularis, S., Bennett, J. C. & Corrsin, S. 1978 Velocity-derivative skewness in small Reynolds number, nearly isotropic turbulence. J. Fluid Mech. 88, 63–69.Google Scholar
Tennekes, H. 1968 Simple model for the small-scale structure of turbulence. Phys. Fluids 11, 669–671.Google Scholar
Thiesset, F., Antonia, R. A. & Danaila, L. 2013 Scale-by-scale turbulent energy budget in the intermediate wake of two-dimensional generators. Phys. Fluids 25, 115105.CrossRefGoogle Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.Google Scholar
Van Atta, C. W. & Antonia, R. A. 1980 Reynolds number dependence of skewness and flatness factors of turbulent velocity derivatives. Phys. Fluids 23, 252–257.Google Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.Google Scholar
Zhou, Y., Antonia, R. A. & Tsang, W. K. 1998 The effect of Reynolds number on a turbulent far-wake. Exp. Fluids 25, 118–125.Google Scholar
Zhou, Y., Antonia, R. A. & Tsang, W. K. 1999 The effect of the Reynolds number on the Reynolds stresses and vorticity in a turbulent far-wake. Exp. Therm. Fluid Sci. 18, 291–298.Google Scholar