Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T22:41:12.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Trapped continental shelf waves with a free surface

Published online by Cambridge University Press:  30 September 2020

G. Kaoullas Open the ORCID record for G. Kaoullas [Opens in a new window]  and
E. R. Johnson Open the ORCID record for E. R. Johnson [Opens in a new window]
G. Kaoullas*
Affiliation:
Department of Mathematics and Statistics, University of Cyprus, Nicosia, Cyprus
E. R. Johnson
Affiliation:
Department of Mathematics, University College London, London WC1H 0AY, UK
*
†Email address for correspondence: g.kaoullas@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

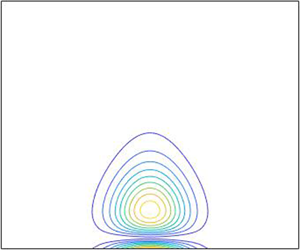
A number of recent results have shown that within the shallow water, rigid-lid approximation, alongshore variations in the bathymetry, i.e. a submerged ridge, can lead to continental shelf waves (CSWs) that are localised geographically at the ridge and then decay both along and away from the coast. Removing the rigid-lid assumption, introduces the superinertial Poincaré waves and a Kelvin wave that is present at all frequencies. This implies that the spectrum of the associated wave operator, which is bounded for the rigid lid case, is continuous and unbounded for the free-surface case. In the rigid-lid case the localisation of modes are isolated eigenvalues lying above the continuous spectrum whereas any localised modes for the free-surface problem must necessarily be embedded in the continuous spectrum. The purpose of this work is to construct trapped CSWs analytically and numerically for a non-rectilinear shelf. A regular asymptotic method is employed by considering a slowly varying, non-rectilinear shelf with an approximate boundary condition at the shelf–ocean boundary. It is shown that even with the free-surface present, trapped CSWs do indeed exist for the submerged ridge topography. Comparison with highly accurate numerical results demonstrates the accuracy of the asymptotic method and also allows the consideration of shelves that abut an open ocean so avoiding the approximate boundary condition at the shelf–ocean boundary.

JFM classification

Geophysical and Geological Flows: Shallow water flows Geophysical and Geological Flows: Topographic effects
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 903 , 25 November 2020 , A36
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, J. K. & Buchwald, V. T. 1969 The generation of continental shelf waves. J. Fluid Mech. 35 (4), 815–826.CrossRefGoogle Scholar
Advanpix 2019 Multiprecision Computing Toolbox for MATLAB. Available at: www.advanpix.com.Google Scholar
Aslanyan, A., Parnovski, L. & Vassiliev, D. 2000 Complex resonances in acoustic waveguides. Q. J. Mech. Appl. Maths 53 (3), 429–447.CrossRefGoogle Scholar
Brink, K. H. 1991 Coastal-trapped waves and wind-driven currents over the continental shelf. Annu. Rev. Fluid Mech. 23 (1), 389–412.CrossRefGoogle Scholar
Buchwald, V. T. & Adams, J. K. 1968 The propagation of continental shelf waves. Proc. R. Soc. Lond. A 305 (1481), 235–250.Google Scholar
Chapman, D. C. 1983 On the influence of stratification and continental shelf and slope topography on the dispersion of subinertial coastally trapped waves. J. Phys. Oceanogr. 13 (9), 1641–1652.2.0.CO;2>CrossRefGoogle Scholar
Davies, E. B. & Parnovski, L. 1998 Trapped modes in acoustic waveguides. Q. J. Mech. Appl. Maths 51 (3), 477–492.CrossRefGoogle Scholar
Dittrich, J. & Kriz, J. 2002 Curved planar quantum wires with Dirichlet and Neumann boundary conditions. J. Phys. A 35 (20), L269–L275.CrossRefGoogle Scholar
Duclos, P. & Exner, P. 1995 Curvature-induced bound states in quantum waveguides in two and three dimensions. Rev. Math. Phys. 7, 73–102.CrossRefGoogle Scholar
Evans, D. V., Levitin, M. & Vassiliev, D. 1994 Existence theorems for trapped modes. J. Fluid Mech. 261, 21–31.CrossRefGoogle Scholar
Exner, P. & Seba, P. 1989 Bound states in curved quantum waveguides. J. Math. Phys. 30 (11), 2574–2580.CrossRefGoogle Scholar
Gridin, D., Craster, R. V. & Adamou, A. T. I. 2005 Trapped modes in curved elastic plates. Proc. R. Soc. Lond. A 461 (2064), 1181–1197.Google Scholar
Grimshaw, R. 1977 The effects of a variable coriolis parameter, coastline curvature and variable bottom topography on continental shelf waves. J. Phys. Oceanogr. 7 (4), 547–554.2.0.CO;2>CrossRefGoogle Scholar
Huthnance, J. M. 1975 On trapped waves over a continental shelf. J. Fluid Mech. 69 (4), 689–704.CrossRefGoogle Scholar
Huthnance, J. M. 1978 Coastal trapped waves - analysis and numerical-calculation by inverse iteration. J. Phys. Oceanogr. 8 (1), 74–92.2.0.CO;2>CrossRefGoogle Scholar
Huthnance, J. M. 1987 Effects of longshore shelf variations on barotropic continental shelf waves, slope currents and ocean modes. Prog. Oceanogr. 19 (2), 177–220.CrossRefGoogle Scholar
Johnson, E. R. 1989 Topographic waves in open domains. Part 1. Boundary conditions and frequency estimates. J. Fluid Mech. 200, 69–76.CrossRefGoogle Scholar
Johnson, E. R. & Kaoullas, G. 2011 Bay-trapped low-frequency oscillations in lakes. Geophys. Astrophys. Fluid Dyn. 105 (1), 48–60.CrossRefGoogle Scholar
Johnson, E. R., Levitin, M. & Parnovski, L. 2006 Existence of eigenvalues of a linear operator pencil in a curved waveguide—localized shelf waves on a curved coast. SIAM J. Math. Anal. 37 (5), 1465–1481.CrossRefGoogle Scholar
Kaoullas, G. & Johnson, E. R. 2010 a Fast accurate computation of shelf waves for arbitrary depth profiles. Cont. Shelf Res. 30 (7), 833–836.CrossRefGoogle Scholar
Kaoullas, G. & Johnson, E. R. 2010 b Geographically localised shelf waves on curved coasts. Cont. Shelf Res. 30 (15), 1753–1760.CrossRefGoogle Scholar
Kaoullas, G. & Johnson, E. R. 2012 Isobath variation and trapping of continental shelf waves. J. Fluid Mech. 700, 283–303.CrossRefGoogle Scholar
Kaplunov, J. D., Rogerson, G. A. & Tovstik, P. E. 2005 Localized vibration in elastic structures with slowly varying thickness. Q. J. Mech. Appl. Maths 58 (4), 645–664.CrossRefGoogle Scholar
Krejčiřík, D. & Kříž, J. 2005 On the spectrum of curved planar waveguides. Publ. Res. Inst. Math. Sci. 41 (3), 757–791.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1991 Quantum Mechanics Non-Relativistic Theory, vol. 3. Butterworth-Heinemann.Google Scholar
LeBlond, P. H. & Mysak, L. A. 1978 Waves in the Ocean. Elsevier.Google Scholar
Linton, C. & McIver, M. 1998 Trapped modes in cylindrical waveguides. Q. J. Mech. Appl. Maths 51, 389–412.CrossRefGoogle Scholar
Linton, C. M. & McIver, P. 2007 Embedded trapped modes in water waves and acoustics. Wave Motion 45 (1), 16–29.CrossRefGoogle Scholar
Mysak, L. A. 1980 Recent advances in shelf wave dynamics. Rev. Geophys. Space Phys. 18 (1), 211–241.CrossRefGoogle Scholar
Postnova, J. & Craster, R. V. 2008 Trapped modes in elastic plates, ocean and quantum waveguides. Wave Motion 45 (4), 565–579.CrossRefGoogle Scholar
Proudman, J. 1929 On a general expansion in the theory of the tides. Proc. Lond. Math. Soc. s2-29 (1), 527–536.CrossRefGoogle Scholar
Rhines, P. 1969 Slow oscillations in an ocean of varying depth. Part 1. Abrupt topography. J. Fluid Mech. 37, 161–189.CrossRefGoogle Scholar
Robinson, A. R. 1964 Continental shelf waves and the response to of sea level to weather systems. J. Geophys. Res. 69 (2), 367–368.CrossRefGoogle Scholar
Rocha, C. B., Bossy, T., Llewellyn Smith, S. G. & Young, W. R. 2020 Improved bounds on horizontal convection. J. Fluid Mech. 883, A41.CrossRefGoogle Scholar
Rodney, J. T. & Johnson, E. R. 2012 Localisation of coastal trapped waves by longshore variations in bottom topography. Cont. Shelf Res. 32, 130–137.CrossRefGoogle Scholar
Rodney, J. T. & Johnson, E. R. 2015 Localised continental shelf waves: geometric effects and resonant forcing. J. Fluid Mech. 785, 54–77.CrossRefGoogle Scholar
Schulz, William J., Mied, Richard P. & Snow, Charlotte M. 2012 Continental shelf wave propagation in the mid-atlantic bight: a general dispersion relation. J. Phys. Oceanogr. 42 (4), 558–568.CrossRefGoogle Scholar
Shen, J. & Wang, L.-L. 2009 Some recent advances on spectral methods for unbounded domains. Commun. Comput. Phys. 5 (2–4), 195–241.Google Scholar
Tang, T. 1993 The Hermite spectral method for Gaussian-type functions. SIAM J. Sci. Comput. 14 (3), 594–606.CrossRefGoogle Scholar
Tisseur, F. 2000 Backward error and condition of polynomial eigenvalue problems. Linear Algebr. Applics. 309 (1), 339–361.CrossRefGoogle Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
Weideman, J. A. C. & Reddy, S. C. 2000 A MATLAB differentiation matrix suite. ACM Trans. Math. Softw. 26 (4), 465–519.CrossRefGoogle Scholar