Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T22:47:34.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Trigger turbulent bands directly at low Reynolds numbers in channel flow using a moving-force technique

Published online by Cambridge University Press:  02 October 2020

Baofang Song Open the ORCID record for Baofang Song [Opens in a new window]  and
Xiangkai Xiao
Baofang Song*
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin300072, PR China
Xiangkai Xiao
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin300072, PR China
*
†Email address for correspondence: baofang_song@tju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

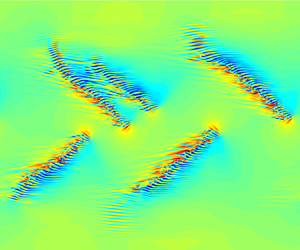
We show a method, for direct numerical simulations, to trigger and maintain turbulent bands directly at low Reynolds numbers in channel flow. The key is to impose a moving localised force which induces a local flow with sufficiently strong inflectional instability. With the method, we can trigger and maintain turbulent bands at Reynolds numbers down to $Re\simeq 500$. More importantly, we can generate any band patterns with desired relative position and orientation. The usual perturbation approach resorts to turbulent fields simulated at higher Reynolds numbers, random noise or localised vortical perturbation, which neither assures a successful generation of bands at low Reynolds numbers nor offers a control on the orientation of the generated bands. A precise control on the position and orientation of turbulent bands is important for the investigation of all possible types of band interaction at low Reynolds numbers and for understanding the subcritical transition in channel flow.

JFM classification

Instability: Transition to turbulence Nonlinear Dynamical Systems: Pattern formation Turbulent Flows: Intermittency
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 903 , 25 November 2020 , A43
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57, 1435–1458.CrossRefGoogle Scholar
Barkley, D. & Tuckerman, L. S. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94, 014502.CrossRefGoogle ScholarPubMed
Chai, C. & Song, B. 2019 Stability of slip channel flow revisited. Phys. Fluids 31, 084105.Google Scholar
Chantry, M., Tuckerman, L. S. & Barkley, D. 2017 Universal continuous transition to turbulence in a planar shear flow. J. Fluid Mech. 824, R1.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 3, 385–425.CrossRefGoogle Scholar
Dauchaot, O. & Daviaud, F. 1995 Finite amplitude perturbation and spots growth mechanism in plane Couette flow. Phys. Fluids 7, 335.CrossRefGoogle Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502.CrossRefGoogle ScholarPubMed
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.CrossRefGoogle Scholar
Henningson, D. S. 1989 Wave growth and spreading of a turbulent spot in plane Poiseuille flow. Phys. Fluids A 1, 1876.CrossRefGoogle Scholar
Henningson, D. S. & Alfredsson, P. H. 1987 The wave structure of turbulent spots in plane Poiseuille flow. J. Fluid Mech. 178, 405–421.CrossRefGoogle Scholar
Henningson, D. S. & Kim, J. 1991 On turbulent spots in plane Poiseuille flow. J. Fluid Mech. 228, 183–205.Google Scholar
Hof, B., De Lozar, A., Avila, M., Tu, X. & Schneider, T. M. 2010 Eliminating turbulence in spatially intermittent flows. Science 327, 1491–1494.CrossRefGoogle ScholarPubMed
Hugues, S. & Randriamampianina, A. 1998 An improved projection scheme applied to pseudospectral methods for the incompressible Navier–Stokes equations. Intl J. Num. Meth. Fluids 28, 501–521.3.0.CO;2-S>CrossRefGoogle Scholar
Kanazawa, T. 2018 Lifetime and growing process of localized turbulence in plane channel flow. PhD thesis, Osaka University.Google Scholar
Paranjape, C. S., Duguet, Y. & Hof, B. 2020 Oblique stripe solutions of channel flow. J. Fluid Mech. 897, A7.CrossRefGoogle Scholar
Prigent, A., Gregoire, G., Chate, H., Dauchot, O. & van Saarloos, W. 2002 Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 89, 014501.CrossRefGoogle ScholarPubMed
Reetz, F., Kreilos, T. & Schneider, T. M. 2019 Exact invariant solution reveals the origin of self-organized oblique turbulent–laminar stripes. Nat. Commun. 10, 2271.CrossRefGoogle ScholarPubMed
Rolland, J. 2015 Formation of spanwise vorticity in oblique turbulent bands of transitional plane Couette flow, part 1: numerical experiments. Eur. J. Mech. (B/ Fluids) 50, 52–59.CrossRefGoogle Scholar
Rolland, J. 2016 Formation of spanwise vorticity in oblique turbulent bands of transitional plane Couette flow, part 2: modelling and stability analysis. Eur. J. Mech. (B/ Fluids) 56, 13–27.CrossRefGoogle Scholar
Sano, M. & Tamai, K. 2016 A universal transition to turbulence in channel flow. Nat. Phys. 12, 249–253.CrossRefGoogle Scholar
Shimizu, M. & Manneville, P. 2019 Bifurcations to turbulence in transitional channel flow. Phys. Rev. Fluids 4, 113903.CrossRefGoogle Scholar
Tao, J. J., Eckhardt, B. & Xiong, X. M. 2018 Extended localized structures and the onset of turbulence in channel flow. Phys. Rev. Fluids 3, 011902.CrossRefGoogle Scholar
Tao, J. & Xiong, X. 2014 The unified transition stages in linearly stable shear flows. In Proceedings of the 14th Asian Congress of Fluid Mechanics-14ACFM, Hanoi and Halong, Vietnam, pp. 55–62.Google Scholar
Tsukahara, T., Iwamoto, K., Kawamura, H. & Takeda, T. 2014 a DNS of heat transfer in a transitional channel flow accompanied by a turbulent puff-like structure. arXiv:1406.0586v2.Google Scholar
Tsukahara, T., Kawaguchi, Y. & Kawamura, H. 2014 b An experimental study on turbulent-stripe structure in transitional channel flow. arXiv:1406.1378.Google Scholar
Tsukahara, T. & Kawamura, H. 2014 Turbulent heat transfer in a channel flow at transitional Reynolds numbers. arXiv:1406.0959v1.Google Scholar
Tsukahara, T., Seki, Y., Kawamura, H. & Tochio, D. 2005 DNS of turbulent channel flow at very low Reynolds numbers. In Proceedings of Fourth International Symposium on Turbulence and Shear Flow Phenomena, Williamsburg, USA, pp. 935–940.Google Scholar
Tuckerman, L. & Barkley, D. 2011 Patterns and dynamics in transitional plane Couette flow. Phys. Fluids 23, 041301.CrossRefGoogle Scholar
Tuckerman, L. S., Chantry, M. & Barkley, D. 2020 Patterns in wall-bounded shear flows. Annu. Rev. Fluid Mech. 52, 343–67.CrossRefGoogle Scholar
Tuckerman, L. S., Kreilos, T., Shrobsdorff, H., Schneider, T. M. & Gibson, J. F. 2014 Turbulent–laminar patterns in plane Poiseuille flow. Phys. Fluids 26, 114103.CrossRefGoogle Scholar
Willis, A. P. 2017 The openpipeflow Navier–Stokes solver. SoftwareX 6, 124–127.CrossRefGoogle Scholar
Xiao, X. & Song, B. 2020 The growth mechanism of turbulent bands in channel flow at low Reynolds numbers. J. Fluid Mech. 883, R1.CrossRefGoogle Scholar
Xiong, X. M., Tao, J., Chen, S. & Brandt, L. 2015 Turbulent bands in plane-Poiseuille flow at moderate Reynolds numbers. Phys. Fluids 27, 041702.CrossRefGoogle Scholar