Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T04:53:17.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Tunable fall velocity of a dense ball in oscillatory cross-sheared concentrated suspensions

Published online by Cambridge University Press:  04 April 2014

Frédéric Blanc ,
Elisabeth Lemaire  and
François Peters
Frédéric Blanc
Affiliation:
CNRS, Université de Nice, LPMC-UMR 7336, 06108 Nice CEDEX 2, France
Elisabeth Lemaire
Affiliation:
CNRS, Université de Nice, LPMC-UMR 7336, 06108 Nice CEDEX 2, France
François Peters*
Affiliation:
CNRS, Université de Nice, LPMC-UMR 7336, 06108 Nice CEDEX 2, France
*
†Email address for correspondence: Francois.Peters@unice.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The fall velocity of a dense large ball in a suspension of neutrally buoyant non-Brownian particles subjected to horizontal oscillatory shear is studied. As the strain amplitude is increased, the velocity increases up to a maximum value before decreasing to the value that it would have in a resting suspension. The higher the frequency is, the stronger the effect is. The falling ball velocity can be largely increased in the presence of the oscillatory cross-shear flow. For instance, for a particle volume fraction of 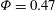$\varPhi =0.47$ it reaches four times the value it has in the unsheared suspension. At small strain amplitudes, it turns out that the velocity of the falling ball is determined by a balance between the steady drag flow, which drives the apparent suspension viscosity toward a high value, and the oscillatory cross-shear, which lessens it. A simple model is proposed to explain the experimental observations at small strain amplitude. The velocity decrease observed at larger amplitude is not completely understood yet.

JFM classification

Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 746 , 10 May 2014 , R4
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barral, Q.2011 Superposition d’écoulements orthogonaux dans des fluides complexes: mise en place de l’expérience, application aux suspensions et aux fluides à seuil. PhD thesis, Université Paris-Est.Google Scholar
Blanc, F., Lemaire, E., Meunier, A. & Peters, F. 2013 Microstructure in sheared non-Brownian concentrated suspensions. J. Rheol. 57 (1), 273–292.CrossRefGoogle Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011a Experimental signature of the pair trajectories of rough spheres in the shear-induced microstructure in noncolloidal suspensions. Phys. Rev. Lett. 107 (20), 208302.CrossRefGoogle ScholarPubMed
Blanc, F., Peters, F. & Lemaire, E. 2011b Local transient rheological behavior of concentrated suspensions. J. Rheol. 55 (4), 835–854.CrossRefGoogle Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011c Particle image velocimetry in concentrated suspensions: application to local rheometry. Appl. Rheol. 21, 23735.Google Scholar
Boyer, F., Guazzelli, É. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.CrossRefGoogle ScholarPubMed
Breedveld, V., van den Ende, D., Jongschaap, R. & Mellema, J. 2001 Shear-induced diffusion and rheology of noncolloidal suspensions: time scales and particle displacements. J. Chem. Phys. 114 (13), 5923–5936.CrossRefGoogle Scholar
Bricker, J. M. & Butler, J. E. 2006 Oscillatory shear of suspensions of noncolloidal particles. J. Rheol. 50 (5), 711–728.CrossRefGoogle Scholar
Bricker, J. M. & Butler, J. E. 2007 Correlation between stresses and microstructure in concentrated suspensions of non-Brownian spheres subject to unsteady shear flows. J. Rheol. 51 (4), 735–759.CrossRefGoogle Scholar
Cheng, X., McCoy, J. H., Israelachvili, J. N. & Cohen, I. 2011 Imaging the microscopic structure of shear thinning and thickening colloidal suspensions. Science 333 (6047), 1276–1279.CrossRefGoogle ScholarPubMed
Corte, L., Chaikin, P. M., Gollub, J. P. & Pine, D. J. 2008 Random organization in periodically driven systems. Nat. Phys. 4 (5), 420–424.CrossRefGoogle Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013 Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.CrossRefGoogle Scholar
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24 (6), 799–814.CrossRefGoogle Scholar
Gao, C., Kulkarni, S. D., Morris, J. F. & Gilchrist, J. F. 2010 Direct investigation of anisotropic suspension structure in pressure-driven flow. Phys. Rev. E 81 (4), 041403.CrossRefGoogle ScholarPubMed
Hanotin, C., de Richter, S. K., Marchal, P., Michot, L. J. & Baravian, C. 2012 Vibration-induced liquefaction of granular suspensions. Phys. Rev. Lett. 108 (19), 198301.CrossRefGoogle ScholarPubMed
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics. Martinus Nijhoff.CrossRefGoogle Scholar
Kolli, V. G., Pollauf, E. J. & Gadala-Maria, F. 2002 Transient normal stress response in a concentrated suspension of spherical particles. J. Rheol. 46 (1), 321–334.CrossRefGoogle Scholar
Lin, Y., Phan-Thien, N. & Khoo, B. C. 2013 Short-term and long-term irreversibility in particle suspensions undergoing small and large amplitude oscillatory stress. J. Rheol. 57 (5), 1325–1346.CrossRefGoogle Scholar
Mondy, L. A., Graham, A. L. & Jensen, J. L. 1986 Continuum approximations and particle interactions in concentrated suspensions. J. Rheol. 30 (5), 1031–1052.CrossRefGoogle Scholar
Morris, J. F. 2009 A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 48 (8), 909–923.CrossRefGoogle Scholar
Narumi, T., See, H., Honma, Y., Hasegawa, T., Takahashi, T. & Phan-Thien, N. 2002 Transient response of concentrated suspensions after shear reversal. J. Rheol. 46 (1), 295–305.CrossRefGoogle Scholar
Ovarlez, G., Bertrand, F., Coussot, P. & Chateau, X. 2012 Shear-induced sedimentation in yield stress fluids. J. Non-Newtonian Fluid Mech. 177, 19–28.CrossRefGoogle Scholar
Padhy, S., Shaqfeh, E. S. G., Iaccarino, G., Morris, J. F. & Tonmukayakul, N. 2013 Simulations of a sphere sedimenting in a viscoelastic fluid with cross-shear flow. J. Non-Newtonian Fluid Mech. 197, 48–60.CrossRefGoogle Scholar
Park, H.-O., Bricker, J. M., Roy, M. J. & Butler, J. E. 2011 Rheology of oscillating suspensions of noncolloidal spheres at small and large accumulated strains. Phys. Fluids 23, 013302.CrossRefGoogle Scholar
Parsi, F. & Gadala-Maria, F. 1987 Fore-and-aft asymmetry in a concentrated suspension of solid spheres. J. Rheol. 31 (8), 725–732.CrossRefGoogle Scholar
Pine, D. J., Gollub, J. P., Brady, J. F.. & Leshansky, A. M. 2005 Chaos and threshold for irreversibility in sheared suspensions. Nature 438 (7070), 997–1000.CrossRefGoogle ScholarPubMed
Rampall, I., Smart, J. R. & Leighton, D. T. 1997 The influence of surface roughness on the particle-pair distribution function of dilute suspensions of non-colloidal spheres in simple shear flow. J. Fluid Mech. 339, 1–24.CrossRefGoogle Scholar
Reardon, P. T., Graham, A. L., Feng, S., Chawla, V., Admuthe, R. S. & Mondy, L. A. 2007 Non-Newtonian end effects in falling ball viscometry of concentrated suspensions. Rheol. Acta 46 (3), 413–424.CrossRefGoogle Scholar
Sierou, A. & Brady, J. F. 2002 Rheology and microstructure in concentrated noncolloidal suspensions. J. Rheol. 46 (5), 1031–1056.CrossRefGoogle Scholar
Stokes, G. G. 1851 On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 9, 8.Google Scholar
Van den Brule, B. H. A. A. & Gheissary, G. 1993 Effects of fluid elasticity on the static and dynamic settling of a spherical particle. J. Non-Newtonian Fluid Mech. 49 (1), 123–132.CrossRefGoogle Scholar
Yeo, K. & Maxey, M. R. 2010 Dynamics of concentrated suspensions of non-colloidal particles in Couette flow. J. Fluid Mech. 649 (1), 205–231.CrossRefGoogle Scholar
Supplementary material: PDF

Blanc supplementary material

Supplementary figure

Download Blanc supplementary material(PDF)
PDF 60.1 KB
Supplementary material: PDF

Blanc supplementary material

Supplementary material

Download Blanc supplementary material(PDF)
PDF 47.5 KB