Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Yan
Dong, Quanlin
and
Wang, Pengfei
2015.
Numerical Investigation on Fluid Flow in a 90-Degree Curved Pipe with Large Curvature Ratio.
Mathematical Problems in Engineering,
Vol. 2015,
Issue. ,
p.
1.
Ault, Jesse T.
Chen, Kevin K.
and
Stone, Howard A.
2015.
Downstream decay of fully developed Dean flow.
Journal of Fluid Mechanics,
Vol. 777,
Issue. ,
p.
219.
Carlsson, C.
Alenius, E.
and
Fuchs, L.
2015.
Swirl switching in turbulent flow through 90° pipe bends.
Physics of Fluids,
Vol. 27,
Issue. 8,
Kalpakli Vester, Athanasia
Örlü, Ramis
and
Alfredsson, P. Henrik
2015.
POD analysis of the turbulent flow downstream a mild and sharp bend.
Experiments in Fluids,
Vol. 56,
Issue. 3,
Grega, Lisa
Kothari, Manthan
Specian, Andrew
and
Voinier, Steven
2015.
Characterization of Flow Within a Fuel Cell Manifold Subject to Asymmetric Inlet Conditions.
Journal of Fuel Cell Science and Technology,
Vol. 12,
Issue. 6,
Vester, Athanasia Kalpakli
Örlü, Ramis
and
Alfredsson, P. Henrik
2015.
Pulsatile Turbulent Flow in Straight and Curved Pipes – Interpretation and Decomposition of Hot-Wire Signals.
Flow, Turbulence and Combustion,
Vol. 94,
Issue. 2,
p.
305.
Chen, X.
Le, T.
Ewing, D.
and
Ching, C. Y.
2016.
Effect of bend separation distance on the mass transfer in back-to-back pipe bends arranged in a 180° configuration.
Heat and Mass Transfer,
Vol. 52,
Issue. 12,
p.
2687.
Ali, SK Zeeshan
and
Dey, Subhasish
2016.
Entry flow in curved pipes: turbulent boundary layer approach.
Journal of Hydraulic Research,
Vol. 54,
Issue. 1,
p.
90.
Noorani, A.
and
Schlatter, P.
2016.
Swirl-switching phenomenon in turbulent flow through toroidal pipes.
International Journal of Heat and Fluid Flow,
Vol. 61,
Issue. ,
p.
108.
Kalpakli Vester, Athanasia
Sattarzadeh, Sohrab S.
and
Örlü, Ramis
2016.
Combined hot-wire and PIV measurements of a swirling turbulent flow at the exit of a 90° pipe bend.
Journal of Visualization,
Vol. 19,
Issue. 2,
p.
261.
Gil-Prieto, Daniel
Zachos, Pavlos
MacManus, David G.
and
Tanguy, Geoffrey
2016.
Convoluted Intake Distortion Measurements Using Stereo Particle Image Velocimetry.
Kalpakli Vester, Athanasia
Örlü, Ramis
and
Alfredsson, P. Henrik
2016.
Turbulent Flows in Curved Pipes: Recent Advances in Experiments and Simulations.
Applied Mechanics Reviews,
Vol. 68,
Issue. 5,
Tunstall, R.
Laurence, D.
Prosser, R.
and
Skillen, A.
2016.
Large eddy simulation of a T-Junction with upstream elbow: The role of Dean vortices in thermal fatigue.
Applied Thermal Engineering,
Vol. 107,
Issue. ,
p.
672.
Talaat, Waleed M.
Hafez, K.A.
and
Banawan, A.A.
2017.
A CFD presentation and visualization for a new model that uses interceptors to harness hydro-energy at the wash of fast boats.
Ocean Engineering,
Vol. 130,
Issue. ,
p.
542.
Canton, Jacopo
Örlü, Ramis
and
Schlatter, Philipp
2017.
Characterisation of the steady, laminar incompressible flow in toroidal pipes covering the entire curvature range.
International Journal of Heat and Fluid Flow,
Vol. 66,
Issue. ,
p.
95.
Wang, Zhixin
Örlü, Ramis
Schlatter, Philipp
and
Chung, Yongmann M.
2018.
Direct numerical simulation of a turbulent 90° bend pipe flow.
International Journal of Heat and Fluid Flow,
Vol. 73,
Issue. ,
p.
199.
OKI, Junichi
KUGA, Yukika
OGATA, Yoichi
NISHIDA, Keiya
YAMAMOTO, Ryo
NAKAMURA, Kazuhiro
YANAGIDA, Haruna
and
YOKOHATA, Hideaki
2018.
Stereo and time-resolved PIV for measuring pulsatile exhaust flow from a motorized engine.
Journal of Fluid Science and Technology,
Vol. 13,
Issue. 1,
p.
JFST0005.
Hufnagel, Lorenz
Canton, Jacopo
Örlü, Ramis
Marin, Oana
Merzari, Elia
and
Schlatter, Philipp
2018.
The three-dimensional structure of swirl-switching in bent pipe flow.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
86.
Esteban, L. B.
Shrimpton, J. S.
and
Ganapathisubramani, B.
2019.
Laboratory experiments on the temporal decay of homogeneous anisotropic turbulence.
Journal of Fluid Mechanics,
Vol. 862,
Issue. ,
p.
99.
Oweis, Ghanem F.
2019.
An in Vitro Flow Model for Cardiovascular Inflammation.
p.
5014.
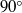 $90{{}^\circ} $ bend
$90{{}^\circ} $ bend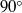 $90{{}^\circ} $ bend at Reynolds numbers between
$90{{}^\circ} $ bend at Reynolds numbers between 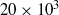 $20\times 1{0}^{3} $ and
$20\times 1{0}^{3} $ and 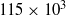 $115\times 1{0}^{3} $. Data were taken at three downstream locations to investigate the evolution of the structures. Snapshot proper orthogonal decomposition (POD) analysis shows that the most energetic structure is not the well-known Dean motion but a bimodal single cell structure with alternating direction of rotation, called the ‘swirl switching’ mode. The strengths of the Dean motion and the swirl-switching structures are similar, indicating that the difference in energy is related to their duration of occurrence, where the Dean motion is associated with a comparatively rapid transition between the two states in the swirl switching mode.
$115\times 1{0}^{3} $. Data were taken at three downstream locations to investigate the evolution of the structures. Snapshot proper orthogonal decomposition (POD) analysis shows that the most energetic structure is not the well-known Dean motion but a bimodal single cell structure with alternating direction of rotation, called the ‘swirl switching’ mode. The strengths of the Dean motion and the swirl-switching structures are similar, indicating that the difference in energy is related to their duration of occurrence, where the Dean motion is associated with a comparatively rapid transition between the two states in the swirl switching mode.

