Article contents
Turbulent vortex pair at equilibrium and its interaction with the ground at 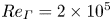 $Re_{\varGamma } = 2 \times 10^5$
$Re_{\varGamma } = 2 \times 10^5$
Published online by Cambridge University Press: 23 May 2024
Abstract
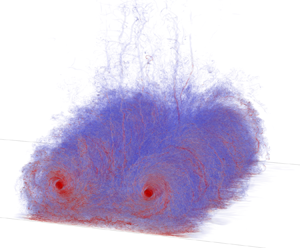
A turbulent two-vortex system (T-2VS) is obtained by inserting analytical model wake vortices into very weak homogeneous isotropic turbulence (HIT) and by evolving them in time using large-eddy simulation until a turbulent state at statistical equilibrium is reached. The T-2VS is characterised as follows: circulation distribution of the vortices; energy of the mean and fluctuating fields; energy dissipation rate. It is also verified that essentially the same T-2VS is obtained when varying the initial model or initial HIT perturbation. A wall-resolved simulation of the T-2VS further interacting with a smooth ground is then performed at  $Re_\varGamma = 2 \times 10^5$; this is
$Re_\varGamma = 2 \times 10^5$; this is  $10 \times$ higher than in previous works, which allows us to better capture the high Reynolds number behaviour. The high release height of the T-2VS also ensures a physically correct approach to the ground. The results are compared with the literature and also to what is obtained for the case of non-turbulent vortices interacting with the same ground at the same Reynolds number. The flow topologies are discussed, and significant differences are highlighted regarding the separation of the boundary layer generated at the ground, and the way this secondary vorticity interacts with the primary vortices and makes them decay. The vortex trajectories are also measured, together with their circulation distribution and global circulation evolution, and the differences are discussed.
$10 \times$ higher than in previous works, which allows us to better capture the high Reynolds number behaviour. The high release height of the T-2VS also ensures a physically correct approach to the ground. The results are compared with the literature and also to what is obtained for the case of non-turbulent vortices interacting with the same ground at the same Reynolds number. The flow topologies are discussed, and significant differences are highlighted regarding the separation of the boundary layer generated at the ground, and the way this secondary vorticity interacts with the primary vortices and makes them decay. The vortex trajectories are also measured, together with their circulation distribution and global circulation evolution, and the differences are discussed.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
Past affiliation: UCLouvain/iMMC.
Past affiliation: UCLouvain/iMMC.
References
- 1
- Cited by


