Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T09:59:11.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Unconfined turbulent entrainment across density interfaces

Published online by Cambridge University Press:  23 September 2014

Ajay B. Shrinivas  and
Gary R. Hunt
Ajay B. Shrinivas
Affiliation:
Department of Civil and Environmental Engineering, Imperial College London, London SW7 2AZ, UK
Gary R. Hunt*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: gary.hunt@eng.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We present theoretical models describing the quasi-steady downward transport of buoyant fluid across a gravitationally stable density interface separating two unbounded quiescent fluid masses. The primary transport mechanism is turbulent entrainment resulting from the localised impingement of a vertically forced high-Reynolds-number axisymmetric jet with steady source conditions. The entrainment across the interface is examined in the large-time asymptotic state, wherein the interfacial gravity current, formed by the fluid entrained from the upper layer and the jet, becomes infinitesimally thin and a two-layer stratification persists. Characterising flows with small interfacial Froude numbers 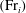$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}({{\mathrm{Fr}}}_i)$ as an axisymmetric semi-ellipsoidal impingement dome, we combine conservation equations with a mechanistic model of entrainment and reveal that, in this regime, the dimensionless entrainment flux 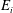$E_i$ across the interface follows the power law 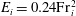$E_i = 0.24{{\mathrm{Fr}}}_i^2$. For large-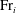${{\mathrm{Fr}}}_i$ impingements, modelled as a fully penetrating turbulent fountain, we show that 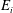$E_i$ no longer scales with 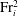${{\mathrm{Fr}}}_i^2$, but linearly on 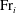${{\mathrm{Fr}}}_i$, following 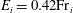$E_i = 0.42{{\mathrm{Fr}}}_i$. We establish the intermediate range of 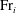${{\mathrm{Fr}}}_i$ over which there is a transition between these quadratic and linear power laws, thus enabling us to classify the dynamics of entrainment across the interface into three distinct regimes. Finally, the close agreement of our solutions with existing experimental results is illustrated.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Convection: Plumes/thermals Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 573 - 598
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ansong, J. K., Kyba, P. K. & Sutherland, B. R. 2008 Fountains impinging on a density interface. J. Fluid Mech. 595, 115–139.Google Scholar
Baines, W. D. 1975 Entrainment by a plume or jet at a density interface. J. Fluid Mech. 68 (2), 309–320.Google Scholar
Baines, W. D., Corriveau, A. F. & Reedman, T. J. 1993 Turbulent fountains in a closed chamber. J. Fluid Mech. 255, 621–646.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bloomfield, L. J. & Kerr, R. C. 2000 A theoretical model of a turbulent fountain. J. Fluid Mech. 424, 197–216.Google Scholar
Cardoso, S. S. S. & Woods, A. W. 1993 Mixing by a turbulent plume in a confined stratified region. J. Fluid Mech. 250, 277–305.Google Scholar
Ching, C. Y., Fernando, H. J. S. & Noh, Y. 1993 Interaction of a negatively buoyant line plume with a density interface. Dyn. Atmos. Oceans 19, 367–388.Google Scholar
Coffey, C. J. & Hunt, G. R. 2010 The unidirectional emptying box. J. Fluid Mech. 660, 456–474.Google Scholar
Cotel, A. J. & Breidenthal, R. E. 1997 A model of stratified entrainment using vortex persistence. Appl. Sci. Res. 57, 349–366.CrossRefGoogle Scholar
Cotel, A. J., Gjestvang, J. A., Ramkhelawan, N. N. & Breidenthal, R. E. 1997 Laboratory experiments of a jet impinging on a stratified interface. Exp. Fluids 23, 155–160.Google Scholar
Cotel, A. J. & Kudo, Y. 2008 Impingement of buoyancy-driven flows at a stratified interface. Exp. Fluids 45, 131–139.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23, 455–493.CrossRefGoogle Scholar
Fernando, H. J. S. & Long, R. R. 1983 The growth of a grid-generated turbulent mixed layer in a two-fluid system. J. Fluid Mech. 133, 377–395.Google Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic Press.Google Scholar
Hunt, G. R. & Coffey, C. J. 2010 Emptying boxes – classifying transient natural ventilation flows. J. Fluid Mech. 646, 137–168.Google Scholar
Kaye, N. B., Flynn, M. R., Cook, M. J. & Ji, Y. 2010 The role of diffusion on the interface thickness in a ventilated filling box. J. Fluid Mech. 652, 195–205.CrossRefGoogle Scholar
Kaye, N. B. & Hunt, G. R. 2006 Weak fountains. J. Fluid Mech. 558, 319–328.CrossRefGoogle Scholar
Kumagai, M. 1984 Turbulent buoyant convection from a source in a confined two-layered region. J. Fluid Mech. 147, 105–131.CrossRefGoogle Scholar
Lin, Y. J. P. & Linden, P. F. 2005 The entrainment due to a turbulent fountain at a density interface. J. Fluid Mech. 542, 25–52.Google Scholar
Linden, P. F. 1973 The interaction of a vortex ring with a sharp density interface: a model for turbulent entrainment. J. Fluid Mech. 60 (3), 467–480.Google Scholar
Linden, P. F. 1975 The deepening of a mixed layer in a stratified fluid. J. Fluid Mech. 71 (2), 385–405.CrossRefGoogle Scholar
McDougall, T. J.1978 Some aspects of geophysical turbulence. PhD thesis, University of Cambridge.Google Scholar
Mizushina, T., Ogino, F., Takeuchi, H. & Ikawa, H. 1982 An experimental study of vertical turbulent jet with negative buoyancy. Wärme-und Stoffübertragung. 16, 15–21.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Rouse, H. & Dodu, J. 1955 Turbulent diffusion across a density discontinuity. La Houille Blanche 10, 522–532.Google Scholar
Shapiro, M. A. 1980 Turbulent mixing within tropopause folds as a mechanism for the exchange of chemical constituents between the stratosphere and troposphere. J. Atmos. Sci. 37, 994–1004.Google Scholar
Shy, S. S. 1995 Mixing dynamics of jet interaction with a sharp density interface. Exp. Therm. Fluid Sci. 10, 355–369.Google Scholar
Turner, J. S. 1966 Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 26 (4), 779–792.Google Scholar
Turner, J. S. 1968 The influence of molecular diffusivity on turbulent entrainment across a density interface. J. Fluid Mech. 33 (4), 639–656.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Williamson, N., Armfield, S. W. & Lin, W. 2011 Forced turbulent fountain flow behaviour. J. Fluid Mech. 671, 535–558.Google Scholar
Zhang, Y., Bellingham, J. G., Godin, M. A. & Ryan, J. P. 2012 Using an autonomous underwater vehicle to track the thermocline based on peak-gradient detection. IEEE J. Ocean. Eng. 37 (3), 544–553.Google Scholar
Zilitinkevich, S. S. 1991 Turbulent Penetrative Convection. Avebury Technical.Google Scholar