Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-11T04:57:17.090Z Has data issue: false hasContentIssue false
  • English
  • Français

A uniform momentum zone–vortical fissure model of the turbulent boundary layer

Published online by Cambridge University Press:  06 November 2018

Juan Carlos Cuevas Bautista ,
Alireza Ebadi ,
Christopher M. White Open the ORCID record for Christopher M. White [Opens in a new window] ,
Gregory P. Chini Open the ORCID record for Gregory P. Chini [Opens in a new window]  and
Joseph C. Klewicki
Juan Carlos Cuevas Bautista
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Alireza Ebadi
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Christopher M. White*
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
Gregory P. Chini
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH 03824, USA
Joseph C. Klewicki
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH 03824, USA Department of Mechanical Engineering, University of Melbourne, Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: chris.white@unh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

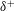Recent studies reveal that at large friction Reynolds number $\unicode[STIX]{x1D6FF}^{+}$ the inertially dominated region of the turbulent boundary layer is composed of large-scale zones of nearly uniform momentum segregated by narrow fissures of concentrated vorticity. Experiments show that, when scaled by the boundary-layer thickness, the fissure thickness is 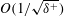$\mathit{O}(1/\sqrt{\unicode[STIX]{x1D6FF}^{+}})$, while the dimensional jump in streamwise velocity across each fissure scales in proportion to the friction velocity 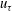$u_{\unicode[STIX]{x1D70F}}$. A simple model that exploits these essential elements of the turbulent boundary-layer structure at large 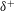$\unicode[STIX]{x1D6FF}^{+}$ is developed. First, a master wall-normal profile of streamwise velocity is constructed by placing a discrete number of fissures across the boundary layer. The number of fissures and their wall-normal locations follow scalings informed by analysis of the mean momentum equation. The fissures are then randomly displaced in the wall-normal direction, exchanging momentum as they move, to create an instantaneous velocity profile. This process is repeated to generate ensembles of streamwise velocity profiles from which statistical moments are computed. The modelled statistical profiles are shown to agree remarkably well with those acquired from direct numerical simulations of turbulent channel flow at large 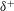$\unicode[STIX]{x1D6FF}^{+}$. In particular, the model robustly reproduces the empirically observed sub-Gaussian behaviour for the skewness and kurtosis profiles over a large range of input parameters.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 609 - 633
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Chauhan, K., Philip, J., deSilva, C. M., Hutchins, N. & Marusic, I. 2014a The turbulent/nonturbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014b Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 298–328.Google Scholar
Chen, C.-H.P. & Blackwelder, R. F. 1978 Large-scale motion in a turbulent boundary layer: a study using temperature contamination. J. Fluid Mech. 89, 1–31.Google Scholar
Chini, G. P., Montemuro, B., White, C. M. & Klewicki, J. C. 2017 A self-sustaining process model of inertial layer dynamics in high Reynolds number turbulent wall flows. Phil. Trans. R. Soc. Lond. A 375, 20160090.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Technical Note 1244.Google Scholar
Eisma, J., Westerweel, J., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27 (5), 55103.Google Scholar
Eyink, G. L. 2008 Turbulent flow in pipes and channels as cross-stream ‘inverse cascades’ of vorticity. Phys. Fluids 20, 125101.Google Scholar
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2003 Thin shear layers in high Reynolds number turbulence – DNS results. Flow Turbul. Combust. 91, 895–929.Google Scholar
Jimenez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–339.Google Scholar
Johansson, A. V. & Alfredsson, P. H. 1991 Evolution and dynamics of shear-layer structures in near-wall turbulence. J. Fluid Mech. 224, 579–599.Google Scholar
Klewicki, J. 2010 Reynolds number dependence, scaling and dynamics of turbulent boundary layers. J. Fluids Engng 132, 094001.Google Scholar
Klewicki, J. C. 2013a On the singular nature of turbulent boundary layers. Procedia IUTAM 9, 69–78.Google Scholar
Klewicki, J. C. & Falco, R. E. 1996 Spanwise vorticity structure in turbulent boundary layers. Intl J. Heat Fluid Flow 17, 363–376.Google Scholar
Klewicki, J. C., Falco, R. E. & Foss, J. F. 1992 Some characteristics of the vortical motions in the outer region of turbulent boundary layers. J. Fluids Engng 114, 530–536.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Klewicki, J., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365 (1852), 823–839.Google Scholar
Klewicki, J. C. & Hirschi, C. R. 2004 Flow field properties local to near-wall shear layers in a low Reynolds number turbulent boundary layer. Phys. Fluids 16, 4163.Google Scholar
Klewicki, J. C., Metzger, M. M., Kelner, E. & Thurlow, E. 1995 Viscous sublayer flow visualizations at R 𝜃 ≃ 1 500 000. Phys. Fluids 7, 857.Google Scholar
Klewicki, J. & Oberlack, M. 2015 Finite Reynolds number properties of a turbulent channel flow similarity solution. Phys. Fluids 27 (9), 095110.Google Scholar
Klewicki, J., Philip, J., Marusic, I., Chauhan, K. & Morrill-Winter, C. 2014 Self-similarity in the inertial region of wall turbulence. Phys. Rev. E 90, 063015.Google Scholar
Klewicki, J. C 2013b A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.Google Scholar
Klewicki, J. C. 2013c Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.Google Scholar
Klewicki, J. C & Hill, R. B. 1998 Spatial structure of negative ∂u/∂y in a low R 𝜃 turbulent boundary layer. J. Fluids Engng 120 (4), 772–777.Google Scholar
Kwon, Y. S., Philip, J., deSilva, C. M., Hutchins, N. & Monty, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9, N31.Google Scholar
Marusic, I. & Adrian, R. J. 2010 The eddies and scales of wall turbulence. In Ten Chapters in Turbulence. Cambridge University Press.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Morrill-Winter, C. & Klewicki, J. 2013 Influences of boundary layer scale separation on the vorticity transport contribution to turbulent inertia. Phys. Fluids 25, 015108.Google Scholar
Morrill-Winter, C. T., Philip, J. & Klewicki, J. C. 2017 An invariant representation of mean inertia: theoretical basis for a log law in turbulent boundary layers. J. Fluid Mech. 813, 594–617.Google Scholar
Morris, S., Stolpa, S., Slaboch, P. & Klewicki, J. 2007 Near-surface particle image velocimetry measurements in a transitionally rough-wall atmospheric boundary layer. J. Fluid Mech. 580, 319–338.Google Scholar
Perlman, E., Burns, R., Li, Y. & Meneveau, C. 2007 Data exploration of turbulence simulations using a database cluster. In Proc. 2007 ACM/IEEE Conf. Supercomputing, p. 23. Association for Computing Machinery.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Priyadarshana, P. J. A., Klewicki, J. C., Treat, S. & Foss, J. F. 2007 Statistical structure of turbulent-boundary-layer velocity-vorticity products at high and low Reynolds numbers. J. Fluid Mech. 570, 307–346.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.Google Scholar
de Silva, C. M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.Google Scholar
Sreenivasan, K. R. & Bershadskii, A. 2006 Finite-Reynolds-number effects in turbulence using logarithmic expansions.. J. Fluid Mech. 554, 477–498.Google Scholar
Taylor, G. I. 1932 The transport of vorticity and heat through fluids in turbulent motion. Proc. R. Soc. Lond. A 135, 685–702.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent–nonturbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar