 $Re_{\tau }=4000$
$Re_{\tau }=4000$Published online by Cambridge University Press: 21 February 2014
The high-Reynolds-number behaviour of the canonical incompressible turbulent channel flow is investigated through large-scale direct numerical simulation (DNS). A Reynolds number is achieved (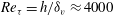 $Re_{\tau } = h/\delta _v \approx 4000$, where
$Re_{\tau } = h/\delta _v \approx 4000$, where 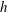 $h$ is the channel half-height, and
$h$ is the channel half-height, and 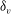 $\delta _v$ is the viscous length scale) at which theory predicts the onset of phenomena typical of the asymptotic Reynolds number regime, namely a sensible layer with logarithmic variation of the mean velocity profile, and Kolmogorov scaling of the velocity spectra. Although higher Reynolds numbers can be achieved in experiments, the main advantage of the present DNS study is access to the full three-dimensional flow field. Consistent with refined overlap arguments (Afzal & Yajnik, J. Fluid Mech. vol. 61, 1973, pp. 23–31; Jiménez & Moser, Phil. Trans. R. Soc. Lond. A, vol. 365, 2007, pp. 715–732), our results suggest that the mean velocity profile never achieves a truly logarithmic profile, and the logarithmic diagnostic function instead exhibits a linear variation in the outer layer whose slope decreases with the Reynolds number. The extrapolated value of the von Kármán constant is
$\delta _v$ is the viscous length scale) at which theory predicts the onset of phenomena typical of the asymptotic Reynolds number regime, namely a sensible layer with logarithmic variation of the mean velocity profile, and Kolmogorov scaling of the velocity spectra. Although higher Reynolds numbers can be achieved in experiments, the main advantage of the present DNS study is access to the full three-dimensional flow field. Consistent with refined overlap arguments (Afzal & Yajnik, J. Fluid Mech. vol. 61, 1973, pp. 23–31; Jiménez & Moser, Phil. Trans. R. Soc. Lond. A, vol. 365, 2007, pp. 715–732), our results suggest that the mean velocity profile never achieves a truly logarithmic profile, and the logarithmic diagnostic function instead exhibits a linear variation in the outer layer whose slope decreases with the Reynolds number. The extrapolated value of the von Kármán constant is 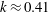 $k \approx 0.41$. A near logarithmic layer is observed in the spanwise velocity variance, as predicted by Townsend’s attached eddy hypothesis, whereas the streamwise variance seems to exhibit a shoulder, perhaps being still affected by low-Reynolds-number effects. Comparison with previous DNS data at lower Reynolds number suggests enhancement of the imprinting effect of outer-layer eddies onto the near-wall region. This mechanisms is associated with excess turbulence kinetic energy production in the outer layer, and it reflects in flow visualizations and in the streamwise velocity spectra, which exhibit sharp peaks in the outer layer. Associated with the outer energy production site, we find evidence of a Kolmogorov-like inertial range, limited to the spanwise spectral density of
$k \approx 0.41$. A near logarithmic layer is observed in the spanwise velocity variance, as predicted by Townsend’s attached eddy hypothesis, whereas the streamwise variance seems to exhibit a shoulder, perhaps being still affected by low-Reynolds-number effects. Comparison with previous DNS data at lower Reynolds number suggests enhancement of the imprinting effect of outer-layer eddies onto the near-wall region. This mechanisms is associated with excess turbulence kinetic energy production in the outer layer, and it reflects in flow visualizations and in the streamwise velocity spectra, which exhibit sharp peaks in the outer layer. Associated with the outer energy production site, we find evidence of a Kolmogorov-like inertial range, limited to the spanwise spectral density of  $u$, whereas power laws with different exponents are found for the other spectra. Finally, arguments are given to explain the ‘odd’ scaling of the streamwise velocity variances, based on the analysis of the kinetic energy production term.
$u$, whereas power laws with different exponents are found for the other spectra. Finally, arguments are given to explain the ‘odd’ scaling of the streamwise velocity variances, based on the analysis of the kinetic energy production term.