Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T05:10:54.552Z Has data issue: false hasContentIssue false
  • English
  • Français

A versatile taxonomy of low-dimensional vortex models for unsteady aerodynamics

Published online by Cambridge University Press:  12 November 2018

Darwin Darakananda  and
Jeff D. Eldredge Open the ORCID record for Jeff D. Eldredge [Opens in a new window]
Darwin Darakananda
Affiliation:
Mechanical and Aerospace Engineering Department, University of California, Los Angeles, CA 90095, USA
Jeff D. Eldredge*
Affiliation:
Mechanical and Aerospace Engineering Department, University of California, Los Angeles, CA 90095, USA
*
†Email address for correspondence: jdeldre@ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Inviscid vortex models have been demonstrated to capture the essential physics of massively separated flows past aerodynamic surfaces, but they become computationally expensive as coherent vortex structures are formed and the wake is developed. In this work, we present a two-dimensional vortex model in which vortex sheets represent shear layers that separate from sharp edges of the body and point vortices represent the rolled-up cores of these shear layers and the other coherent vortices in the wake. We develop a circulation transfer procedure that enables each vortex sheet to feed its circulation into a point vortex instead of rolling up. This procedure reduces the number of computational elements required to capture the dynamics of vortex formation while eliminating the spurious force that manifests when transferring circulation between vortex elements. By tuning the rate at which the vortex sheets are siphoned into the point vortices, we can adjust the balance between the model’s dimensionality and dynamical richness, enabling it to span the entire taxonomy of inviscid vortex models. This hybrid model can capture the development and subsequent shedding of the starting vortices with insignificant wall-clock time and remain sufficiently low-dimensional to simulate long-time-horizon events such as periodic bluff-body shedding. We demonstrate the viability of the method by modelling the impulsive translation of a wing at various fixed angles of attack, pitch-up manoeuvres that linearly increase the angle of attack from 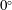$0^{\circ }$ to 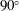$90^{\circ }$, and oscillatory pitching and heaving. We show that the proposed model correctly predicts the dynamics of large-scale vortical structures in the flow by comparing the distributions of vorticity and force responses from results of the proposed model with a model using only vortex sheets and, in some cases, high-fidelity viscous simulation.

JFM classification

Wakes/Jets: Separated flows Vortex Flows: Vortex dynamics Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 917 - 948
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. & Shelley, M. J. 2008 Flapping states of a flag in an inviscid fluid: bistability and the transition to chaos. Phys. Rev. Lett. 100 (7), 074301.Google Scholar
Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Ansari, S. A., Zbikowski, R. & Knowles, K. 2006 Non-linear unsteady aerodynamic model for insect-like flapping wings in the hover. Part 2: Implementation and validation. Proc. Inst. Mech. Engrs 220, 169–186.Google Scholar
Birch, J. M. & Dickinson, M. H. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412 (6848), 729–733.Google Scholar
Brown, C. E. & Michael, W. H. 1954 Effect of leading-edge separation on the lift of a delta wing. J. Aero. Sci. 21 (10), 690–694.Google Scholar
Chorin, A. J. 1990 Hairpin removal in vortex interactions. J. Comput. Phys. 91 (1), 1–21.Google Scholar
Dickinson, M. H. & Götz, K. 1993 Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Exp. Biol. 174, 45–64.Google Scholar
Eldredge, J. D., Wang, C. & Ol, M. V.2009 A computational study of a canonical pitch-up, pitch-down wing maneuver. In 39th AIAA Fluid Dynamics Conference. AIAA Paper 2009-3687.Google Scholar
Fage, A. & Johansen, F. C. 1927 On the flow of air behind an inclined plate of infinite span. Proc. R. Soc. Lond. A 116 (773), 170–197.Google Scholar
Greengard, L. & Rokhlin, V. 1987 A fast algorithm for particle simulations. J. Comput. Phys. 73 (2), 325–348.Google Scholar
Jones, M. A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.Google Scholar
von Kármán, T. & Sears, W. R. 1938 Airfoil theory for non-uniform motion. J. Aero. Sci. 5 (10), 379–390.Google Scholar
Katz, J. 1981 A discrete vortex method for the non-steady separated flow over an airfoil. J. Fluid Mech. 102, 315–328.Google Scholar
Kinsey, T. & Dumas, G. 2008 Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 46 (6), 1318–1330.Google Scholar
Krasny, R. 1986 A study of singularity formation in a vortex sheet by the point-vortex approximation. J. Fluid Mech. 167, 65–93.Google Scholar
Krasny, R. & Nitsche, M. 2002 The onset of chaos in vortex sheet flow. J. Fluid Mech. 454, 47–69.Google Scholar
Li, J. & Wu, Z.-N. 2016 A vortex force study for a flat plate at high angle of attack. J. Fluid Mech. 801, 222–249.Google Scholar
Michelin, S. & Llewellyn Smith, S. G. 2009 An unsteady point vortex method for coupled fluid–solid problems. Theor. Comput. Fluid Dyn. 23, 127–153.Google Scholar
Moore, D. 1979 The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc. R. Soc. Lond. A 365 (1720), 105–119.Google Scholar
Muskhelishvili, N. 2013 Singular Integral Equations, Boundary Problems of Function Theory and Their Application to Mathematical Physics. Dover Publications; corrected reprint of the Noordhoff translation (1953) of the Russian original of 1946.Google Scholar
Nitsche, M., Taylor, M. A. & Krasny, R. 2003 Comparison of regularizations of vortex sheet motion. In Computational Fluid and Solid Mechanics, pp. 1062–1065. Elsevier.Google Scholar
Pullin, D. I. 1978 The large-scale structure of unsteady self-similar rolled-up vortex sheets. J. Fluid Mech. 88 (03), 401–430.Google Scholar
Ramesh, K., Gopalarathnam, A., Edwards, J. R., Ol, M. V. & Granlund, K. 2013 An unsteady airfoil theory applied to pitching motions validated against experiment and computation. Theor. Comput. Fluid Dyn. 27 (6), 843–864.Google Scholar
Ramesh, K., Gopalarathnam, A., Granlund, K., Ol, M. V. & Edwards, J. R. 2014 Discrete-vortex method with novel shedding criterion for unsteady aerofoil flows with intermittent leading-edge vortex shedding. J. Fluid Mech. 751, 500–548.Google Scholar
Rossi, L. F. 1997 Merging computational elements in vortex simulations. SIAM J. Sci. Comput. 18 (4), 1014–1027.Google Scholar
Sarpkaya, T. 1975 An inviscid model of two-dimensional vortex shedding for transient and asymptotically steady separated flow over an inclined plate. J. Fluid Mech. 68, 109–128.Google Scholar
Shukla, R. K. & Eldredge, J. D. 2007 An inviscid model for vortex shedding from a deforming body. Theor. Comput. Fluid Dyn. 21 (5), 343–368.Google Scholar
Taira, K. & Colonius, T. 2007 The immersed boundary method: a projection approach. J. Comput. Phys. 225 (2), 2118–2137.Google Scholar
Taira, K., Dickson, W. B., Colonius, T. & Dickinson, M. H.2007 Unsteadiness in flow over a flat plate at angle-of-attack at low Reynolds numbers. In 45th AIAA Aerosp. Sci. Meet. Exhib. AIAA Paper 2007-0710.Google Scholar
Tchieu, A. & Leonard, A. 2011 A discrete-vortex model for the arbitrary motion of a thin airfoil with fluidic control. J. Fluids Struct. 27 (5–6), 680–693.Google Scholar
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. TR-496.Google Scholar
Wagner, H. 1925 Über die Entstehung des dynamischen Auftriebes von Tragflügeln. Z. Angew. Math. Mech. 5 (1), 17–35.Google Scholar
Wang, C. & Eldredge, J. D. 2013 Low-order phenomenological modeling of leading-edge vortex formation. Theor. Comput. Fluid Dyn. 27 (5), 577–598.Google Scholar
Xia, X. & Mohseni, K. 2013 Lift evaluation of a two-dimensional pitching flat plate. Phys. Fluids 25 (9), 091901.Google Scholar