Published online by Cambridge University Press: 02 November 2021
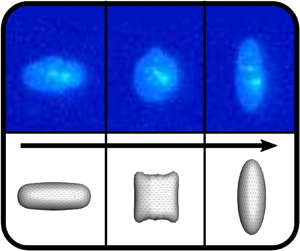
Although the behaviour of fluid-filled vesicles in steady flows has been extensively studied, far less is understood regarding the shape dynamics of vesicles in time-dependent oscillatory flows. Here, we investigate the nonlinear dynamics of vesicles in large amplitude oscillatory extensional (LAOE) flows using both experiments and boundary integral (BI) simulations. Our results characterize the transient membrane deformations, dynamical regimes and stress response of vesicles in LAOE in terms of reduced volume (vesicle asphericity), capillary number ( ${Ca}$, dimensionless flow strength) and Deborah number (
${Ca}$, dimensionless flow strength) and Deborah number ( ${De}$, dimensionless flow frequency). Results from single vesicle experiments are found to be in good agreement with BI simulations across a wide range of parameters. Our results reveal three distinct dynamical regimes based on vesicle deformation: pulsating, reorienting and symmetrical regimes. We construct phase diagrams characterizing the transition of vesicle shapes between pulsating, reorienting and symmetrical regimes within the two-dimensional Pipkin space defined by
${De}$, dimensionless flow frequency). Results from single vesicle experiments are found to be in good agreement with BI simulations across a wide range of parameters. Our results reveal three distinct dynamical regimes based on vesicle deformation: pulsating, reorienting and symmetrical regimes. We construct phase diagrams characterizing the transition of vesicle shapes between pulsating, reorienting and symmetrical regimes within the two-dimensional Pipkin space defined by  ${De}$ and
${De}$ and  ${Ca}$. Contrary to observations on clean Newtonian droplets, vesicles do not reach a maximum length twice per strain rate cycle in the reorienting and pulsating regimes. The distinct dynamics observed in each regime result from a competition between the flow frequency, flow time scale and membrane deformation time scale. By calculating the particle stresslet, we quantify the nonlinear relationship between average vesicle stress and strain rate. Additionally, we present results on tubular vesicles that undergo shape transformation over several strain cycles. Broadly, our work provides new information regarding the transient dynamics of vesicles in time-dependent flows that directly informs bulk suspension rheology.
${Ca}$. Contrary to observations on clean Newtonian droplets, vesicles do not reach a maximum length twice per strain rate cycle in the reorienting and pulsating regimes. The distinct dynamics observed in each regime result from a competition between the flow frequency, flow time scale and membrane deformation time scale. By calculating the particle stresslet, we quantify the nonlinear relationship between average vesicle stress and strain rate. Additionally, we present results on tubular vesicles that undergo shape transformation over several strain cycles. Broadly, our work provides new information regarding the transient dynamics of vesicles in time-dependent flows that directly informs bulk suspension rheology.