Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T06:58:24.043Z Has data issue: false hasContentIssue false
  • English
  • Français

Vibrations of a square cylinder submerged in a wake

Published online by Cambridge University Press:  23 August 2018

Rajesh Bhatt  and
Md. Mahbub Alam Open the ORCID record for Md. Mahbub Alam [Opens in a new window]
Rajesh Bhatt
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Shenzhen Graduate School, Harbin Institute of Technology, 518055 Shenzhen, PR China Digital Engineering Laboratory of Offshore Equipment, Harbin Institute of Technology, 518055 Shenzhen, PR China
Md. Mahbub Alam*
Affiliation:
Institute for Turbulence-Noise-Vibration Interactions and Control, Shenzhen Graduate School, Harbin Institute of Technology, 518055 Shenzhen, PR China Digital Engineering Laboratory of Offshore Equipment, Harbin Institute of Technology, 518055 Shenzhen, PR China
*
†Email addresses for correspondence: alam@hit.edu.cn, alamm28@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

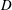A numerical investigation is conducted on the flow around and vibration response of an elastic square cylinder (side width $D$) in the wake of a stationary cylinder at Reynolds numbers of 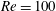$Re=100$ and 200 based on 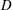$D$ and the free-stream velocity. The downstream cylinder, referred to as the wake cylinder, is allowed to vibrate in the transverse direction only. The reduced velocity 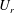$U_{r}$ is varied from 1 to 30. Cylinder centre-to-centre spacing ratios of 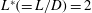$L^{\ast }(=L/D)=2$ and 6 are considered. Simulations are also conducted for a single isolated cylinder, and the results are compared with those for the wake cylinder. The focus is given to vibration response, frequency response, fluctuating lift force, phase relationship between the lift and displacement, work done and the flow structure modification during the cylinder vibration. The results reveal that the dependence of the Strouhal number 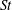$St$ on 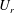$U_{r}$ can distinguish different branches more appropriately than that of the vibration amplitude on $U_{r}$. The vibration response of the single cylinder at 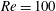$Re=100$ is characterized by the initial, lower and desynchronization branches. On the other hand, that at 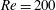$Re=200$ undergoes initial, lower and galloping branches. The galloping involves the characteristics of both the initial and the lower branches or the initial and the desynchronization branches depending on 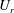$U_{r}$. For the wake cylinder, the gap flow has a significant impact on the vibration response, leading to (i) the absence of galloping at either 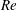$Re$ and 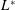$L^{\ast }$, (ii) the presence of an upper branch at 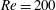$Re=200$, 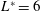$L^{\ast }=6$ and (iii) an initial branch of different characteristics at 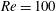$Re=100$, 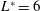$L^{\ast }=6$. The different facets are discussed in terms of wake structures, work done and phase lag between lift and displacement.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 301 - 332
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. M. 2016 Lift forces induced by the phase lag between the vortex sheddings from two tandem bluff bodies. J. Fluids Struct. 65, 217–237.Google Scholar
Alam, M. M. & Kim, S. 2009 Free vibration of two identical circular cylinders in staggered arrangement. Fluid Dyn. Res. 41, 035507.Google Scholar
Alam, M. M. & Meyer, J. P. 2013 Global aerodynamic instability of twin cylinders in cross flow. J. Fluids Struct. 41, 135–145.Google Scholar
Alam, M. M., Moriya, M., Takai, K. & Sakamoto, H. 2002 Suppression of fluid forces acting on two square prisms in a tandem arrangement by passive control of flow. J. Fluids Struct. 16 (8), 1073–1092.Google Scholar
Assi, G. R. S., Bearman, P. W. & Meneghini, J. R. 2010 On the wake-induced vibration of tandem circular cylinders: the vortex interaction excitation mechanism. J. Fluid Mech. 661, 365–401.Google Scholar
Barrero-Gil, A., Sanz-Andres, A. & Roura, M. 2009 Transverse galloping at low Reynolds numbers. J. Fluids Struct. 25, 1236–1242.Google Scholar
Bearman, P. W. & Obasaju, E. D. 1982 An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders. J. Fluid Mech. 119, 297–321.Google Scholar
Blevins, R. D. 1990 Flow Induced Vibration. Van Nostrand Reinhold.Google Scholar
Cui, Z., Zhao, M., Teng, B. & Cheng, L. 2015 Two-dimensional numerical study of vortex-induced vibration and galloping of square and rectangular cylinders in steady flow. Ocean Engng 106, 189–206.Google Scholar
Darekar, R. M. & Sherwin, S. J. 2001 Flow past a square-section cylinder with a wavy stagnation face. J. Fluid Mech. 426, 263–295.Google Scholar
De, A. K. & Dalal, A. 2006 Numerical simulation of unconfined flow past a triangular cylinder. Intl J. Numer. Meth. Fluids 52, 801–821.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
He, T., Zhou, D. & Bao, Y. 2012 Combined interface boundary condition method for fluid–rigid body interaction. Comput. Meth. Appl. Mech. Engng 223–224, 81–102.Google Scholar
Inoue, O., Iwakami, W. & Hatakeyama, N. 2006 Aeolian tones radiated from flow past two square cylinders in a side-by-side arrangement. Phys. Fluids 18, 046104.Google Scholar
Jaiman, R. K., Pillalamarri, N. R. & Guan, M. Z. 2016 A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow. Comput. Meth. Appl. Mech. Engng 301, 187–215.Google Scholar
Joly, A., Etienne, S. & Pelletier, D. 2012 Galloping of square cylinders in cross-flow at low Reynolds numbers. J. Fluids Struct. 28, 232–243.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851.Google Scholar
Kim, S., Alam, M. M., Sakamoto, H. & Zhou, Y. 2009 Flow-induced vibrations of two circular cylinders in tandem arrangement. Part 1. Characteristics of vibration. J. Wind Engng Ind. Aerodyn. 97, 304–311.Google Scholar
Kumar, D., Sing, A. K. & Sen, S. 2018 Identification of response branches for oscillators with curved and straight contours executing VIV. Ocean Engng 164, 616–627.Google Scholar
Ludlam, D. V., Gil, A. B. & Velazquez, A. 2017 Flow-induced vibration of a rotating circular cylinder using position and velocity feedback. J. Fluids Struct. 72, 127–151.Google Scholar
Luo, S. C., Chew, Y. T. & Ng, Y. T. 2003 Characteristics of square cylinder wake transition flows. Phys. Fluids 15 (9), 2549–2559.Google Scholar
Manson, J. R., Pender, G. & Wallis, S. G. 1996 Limitations of traditional finite volume discretizations for unsteady computational fluid dynamics. AIAA J. 34 (5), 1074–1076.Google Scholar
Maruai, N. M., Ali, M. S. M., Ismail, M. H. & Zaki, S. A. 2018 Flow-induced vibration of square cylinder and downstream flat plate associated with micro-scale energy harvester. J. Wind Engng Ind. Aerodyn. 175, 264–282.Google Scholar
Mehmood, A., Abdelkefi, A., Hajj, M. R., Nayfeh, A. H., Akhtar, I. & Uhait, A. O. 2013 Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder. J. Sound Vib. 332, 4656–4667.Google Scholar
Mithun, M. G. & Tiwari, S. 2014 Flow past two tandem square cylinders vibrating transversely in phase. Fluid Dyn. Res. 46, 055509.Google Scholar
More, B. S., Dutta, S., Chauhan, M. K. & Gandhi, B. K. 2015 Experimental investigation of flow behind two tandem square cylinders with oscillating upstream cylinder. Exp. Therm. Fluid Sci. 68, 339–358.Google Scholar
Nakamura, Y. & Hirata, K. 1991 Pressure fluctuations on oscillating rectangular cylinders with the long side normal to the flow. J. Fluids Struct. 5, 165–183.Google Scholar
Nakamura, Y. & Matsukawa, T. 1987 Vortex excitation of rectangular cylinders with a long side normal to the flow. J. Fluid Mech. 180, 171–181.Google Scholar
Nakamura, Y. & Mizota, T. 1975 Unsteady lifts and wakes of oscillating rectangular prisms. ASCE J. Engng Mech. 101, 855–871.Google Scholar
Navrose & Mittal, S. 2017 A new regime of multiple states in free vibration of a cylinder at low Re . J. Fluids Struct. 68, 310–321.Google Scholar
Patankar, S. V. 1980 Numerical Heat Transfer and Fluid Flow. Hemisphere Publishing Corporation, Taylor and Francis Group.Google Scholar
Qin, B., Alam, M. M. & Zhou, Y. 2017 Two tandem cylinders of different diameter in cross-flow: flow-induced vibration. J. Fluid Mech. 829, 621–658.Google Scholar
Robichaux, J., Balachandar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11 (3), 560–578.Google Scholar
Saha, A. K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24, 54–66.Google Scholar
Sahu, A. K., Chhabra, R. P. & Eswaran, V. 2009 Two-dimensional unsteady laminar flow of a power law fluid across a square cylinder. J. Non-Newtonian Fluid Mech. 160, 157–167.Google Scholar
Sakamoto, H., Haniu, H. & Obata, Y. 1987 Fluctuating forces acting on two square prisms in a tandem arrangement. J. Wind Engng Ind. Aerodyn. 26, 85–103.Google Scholar
Sen, S. & Mittal, S. 2011 Free vibration of a square cylinder at low Reynolds numbers. J. Fluids Struct. 27, 875–884.Google Scholar
Sen, S. & Mittal, S. 2015 Effect of mass ratio on free vibrations of a square cylinder at low Reynolds numbers. J. Fluids Struct. 54, 661–678.Google Scholar
Shaaban, M. & Mohany, A. 2018 Flow-induced vibration of three unevenly spaced in-line cylinders in cross-flow. J. Fluids Struct. 76, 367–383.Google Scholar
Sharma, A. & Eswaran, V. 2004 Heat and fluid flow across a square cylinder in the two-dimensional laminar flow regime. Numer. Heat Transf. 45 (3), 247–269.Google Scholar
Singh, A. P., De, A. K., Carpenter, V. K., Eswaran, V. & Muralidhar, K. 2009 Flow past a transversely oscillating square cylinder in free stream at low Reynolds numbers. Intl J. Numer. Meth. Fluids 61, 658–682.Google Scholar
Singh, S. & Biswas, G. 2013 Vortex induced vibrations of a square cylinder at subcritical Reynolds numbers. J. Fluids Struct. 41, 146–155.Google Scholar
Singh, S. P. & Mittal, S. 2005 Vortex-induced oscillations at low Reynolds numbers: hysteresis and vortex-shedding modes. J. Fluids Struct. 20, 1085–1104.Google Scholar
Sohankar, A. 2012 A numerical investigation of the flow over a pair of identical square cylinders in a tandem arrangement. Intl J. Numer. Meth. Fluids 70, 1244–1257.Google Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1997 Numerical simulation of unsteady low-Reynolds number flow around rectangular cylinders at incidence. J. Wind Engng Ind. Aerodyn. 69–71, 189–201.Google Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11 (2), 288–306.Google Scholar
Su, Z., Liu, Y., Zhang, H. & Zhang, D. 2007 Numerical simulation of vortex-induced vibration of a square cylinder. J. Mech. Sci. Tech. 21, 1415–1424.Google Scholar
Zhao, M. 2015 Flow-induced vibrations of square and rectangular cylinders at low Reynolds number. Fluid Dyn. Res. 47, 025502.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2013 Numerical simulation of vortex-induced vibration of a square cylinder at a low Reynolds number. Phys. Fluids 25, 023603.Google Scholar
Zheng, Q. & Alam, M. M. 2017 Intrinsic features of flow past three square prisms in side-by-side arrangement. J. Fluid Mech. 826, 996–1033.Google Scholar
Zheng, Q. & Alam, M. M. 2018 Fluid dynamics around three inline square prisms. J. Fluid Mech. (submitted).Google Scholar