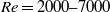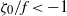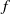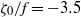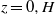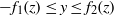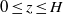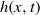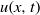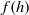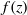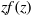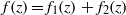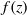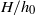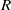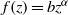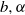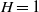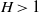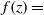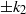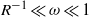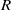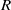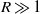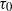We consider the propagation of a high-Reynolds-number gravity current in a horizontal channel along the horizontal coordinate  $x$. The bottom and top of the channel are at
$x$. The bottom and top of the channel are at 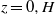 $z= 0, H$, and the cross-section is given by the quite general
$z= 0, H$, and the cross-section is given by the quite general 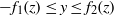 $- {f}_{1} (z)\leq y\leq {f}_{2} (z)$ for
$- {f}_{1} (z)\leq y\leq {f}_{2} (z)$ for 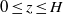 $0\leq z\leq H$. We develop a two-layer shallow-water (SW) formulation, and we implement it for the solution of the dam-break problem. The dependent variables are the position of the interface,
$0\leq z\leq H$. We develop a two-layer shallow-water (SW) formulation, and we implement it for the solution of the dam-break problem. The dependent variables are the position of the interface, 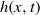 $h(x, t)$, and the velocity (averaged over the area of the current),
$h(x, t)$, and the velocity (averaged over the area of the current), 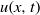 $u(x, t)$. The non-rectangular cross-section geometry enters the formulation via
$u(x, t)$. The non-rectangular cross-section geometry enters the formulation via 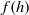 $f(h)$ and integrals of
$f(h)$ and integrals of 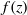 $f(z)$ and
$f(z)$ and 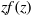 $zf(z)$, where
$zf(z)$, where 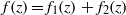 $f(z)= {f}_{1} (z)+ {f}_{2} (z)$ is the width of the channel. For a given geometry
$f(z)= {f}_{1} (z)+ {f}_{2} (z)$ is the width of the channel. For a given geometry 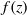 $f(z)$, the free input parameters of the lock-release problem are: (i) the height ratio
$f(z)$, the free input parameters of the lock-release problem are: (i) the height ratio 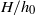 $H/ {h}_{0} $ of ambient to lock; and (ii) the density ratio of ‘light’ to ‘heavy’ fluids,
$H/ {h}_{0} $ of ambient to lock; and (ii) the density ratio of ‘light’ to ‘heavy’ fluids, 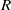 $R$. We show that the dam-break problem is amenable to solution by the method of characteristics, but various complications (internal jumps, critical restrictions) appear when the return flow in the ambient is significant; these features are not captured by a one-layer shallow-water model. The role of the non-standard geometry in the detection and calculation of the internal and reflected jumps, and on the dam-break flow field, is elucidated. The methodology is illustrated for Boussinesq flow in typical geometries: power-law (
$R$. We show that the dam-break problem is amenable to solution by the method of characteristics, but various complications (internal jumps, critical restrictions) appear when the return flow in the ambient is significant; these features are not captured by a one-layer shallow-water model. The role of the non-standard geometry in the detection and calculation of the internal and reflected jumps, and on the dam-break flow field, is elucidated. The methodology is illustrated for Boussinesq flow in typical geometries: power-law (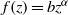 $f(z)= b{z}^{\alpha } $, where
$f(z)= b{z}^{\alpha } $, where 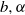 $b, \alpha $ are positive constants), trapezoidal and circle (full or sector); we solved for full-depth (
$b, \alpha $ are positive constants), trapezoidal and circle (full or sector); we solved for full-depth (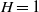 $H= 1$) and part-depth (
$H= 1$) and part-depth (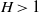 $H\gt 1$) lock-release configurations. The approach seems to work well: in all the tested cases, the solution was obtained with simple mathematical and numerical tools (a Runge–Kutta integrator and a secant-method solver); the insights are compatible with our previous understanding of the problem; and the standard (rectangular) case is recovered in the appropriate limit (i.e. when the side-boundaries of the trapezium cross-section are vertical or far apart). A comparison of the speed of propagation with available experiments is also presented, and the agreement is satisfactory. The present solution is a significant generalization of the classical two-layer gravity–current dam-break problem. The classical formulation for a rectangular (or laterally unbounded) channel is now just a particular case,
$H\gt 1$) lock-release configurations. The approach seems to work well: in all the tested cases, the solution was obtained with simple mathematical and numerical tools (a Runge–Kutta integrator and a secant-method solver); the insights are compatible with our previous understanding of the problem; and the standard (rectangular) case is recovered in the appropriate limit (i.e. when the side-boundaries of the trapezium cross-section are vertical or far apart). A comparison of the speed of propagation with available experiments is also presented, and the agreement is satisfactory. The present solution is a significant generalization of the classical two-layer gravity–current dam-break problem. The classical formulation for a rectangular (or laterally unbounded) channel is now just a particular case, 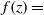 $f(z)= $ const., in the wide domain of cross-sections covered by the new model.
$f(z)= $ const., in the wide domain of cross-sections covered by the new model.