Introduction
Radio-echo sounding (RES) is an active remote-sensing technique that utilizes electromagnetic (EM) waves that penetrate into ice. This technique is used to obtain information about the EM properties of different interfaces that reflect an incident signal back to the acquisition system (Reference Plewes and HubbardPlewes and Hubbard, 2001). RES surveys have been widely employed in Antarctic ice sheet exploration and are considered an indispensable tool for mapping bedrock morphologies and properties. Moreover, the discovery of numerous subglacial lake areas (entrapped in the ice sheet) has attracted scientific interest in the possible existence of water circulation between lakes or beneath the ice (Reference Kapitsa, Ridley, Siegert and ZotikovKapitsa and others, 1996; Reference Testut, Forieri, Bianchi and TabaccoRémy and others, 2003; Reference Tabacco, Cianfarra, Forieri, Salvini and ZirizzottiTabacco and others, 2006; Reference Wingham, Siegert, Shepherd and MuirWingham and others 2006; Reference Bell, Studinger, Shuman, Fahnestock and JoughinBell and others 2007; Reference Carter, Blankenship, Young and HoltCarter and others 2009). While differences in echo strength between rock and lake surfaces can often be clearly differentiated in radargrams (high signal level in a flat shape), this is not true of wet and dry rock surfaces. An increase in signal amplitude from bedrock can be ascribed to several different factors (e.g. a focusing effect, surface roughness, or changes in the EM properties of the ice column). Furthermore, the presence of unconsolidated sediments (water-saturated or not) must be considered as at least probable, which further complicates understanding of the ice/bedrock interface properties.
Observation of the power of radar echoes can help resolve this problem, extending the significance of a RES dataset and enhancing its final interpretation (Reference GogineniOswald and Gogineni, 2008; Reference Paden, Akins, Dunson, Allen and GogineniPaden and others, 2010). In recent years this kind of study has became a powerful tool to investigate and highlight the physical properties of bedrock, with important results that include establishing the presence of different kinds of subglacial lakes, the existence of extensive wet areas, and the possibility of observing hydrological exchange connections under the Antarctic ice sheet (Reference Carter, Blankenship, Peters, Young, Holt and MorseCarter and others, 2007; Reference Zirizzotti, Cafarella and UrbiniZirizzotti and others, 2012). The power of the echoes can be assessed by solving the radar equation that takes into account each term (Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others, 1985), with EM ice absorption, geometrical spreading, medium focusing, and reflectivity being the main contributing factors.
EM ice absorption can be assessed both from ice-core drilling measurements and from RES measurements. Using ice-core drilling data, information can be obtained about ice absorption rate along the ice column. Detailed evaluation can be found in several papers: Reference Carter, Blankenship, Young and HoltCarter and others (2009) analyzed bedrock reflectivity in the Dome C (East Antarctic ice sheet) area using a self-consistent model; Reference Eisen, Wilhelms, Steinhage and SchwanderEisen and others (2006) evaluated RES radargram amplitude with ice-core dielectric profile (DEP)–conductivity measurements from Dronning Maud Land, Antarctica; Reference FujitaFujita and others (2012) studied RES response in East Antarctica; Reference Jacobel, Lapo, Stamp, Youngblood, Welch and BamberJacobel and others (2010) studied radar-attenuated signals in East Antarctica along a traverse route; Reference Matsuoka, Gregor and PattynMatsuoka and others (2012) predicted radar attenuation across the Antarctic ice sheet; Reference MacGregor, Matsuoka, Waddington, Winebrenner and PattynMacGregor and others (2012) examined the spatial variation of radar attenuation in detail for the Vostok (East Antarctica) flowline; and Zirizzotti and others (2010) evaluated ice absorption rate from RES measurements in wet and dry zones in the Dome C area.
This paper aims to integrate and verify ice column absorption (as an important factor in the radar equation) by comparing data from EPICA (European Project for Ice Coring in Antarctica) Dome C ice cores to data obtained from RES echoes recorded over catalogued subglacial lakes (where the EM reflectivity is known) chosen in the area surrounding the ice-core site. The main aim is to investigate how this particular physical property might vary with distance starting from a known calibrated measurement.
Modeling Ice Absorption
In a homogeneous low-loss EM medium with complex relative dielectric permittivity σr = σ′ = − jσ2033;/(σ0ω), the absorption loss rate A (dB m−1) depends on the complex dielectric permittivity according to

where0 and μ 0 are the free-space dielectric permittivity and magnetic permeability respectively, while σ is the electrical conductivity of the media (Reference Ulaby, Moore and FungUlaby and others, 1981). In the case of ice, σ depends on the acidity and temperature while the dielectric permittivity depends on the media temperature and on the frequency of the EM signal.
Different methods have been used to define the absorption loss rate, which has been laboratory-evaluated, by measuring pure ice conductivity at different impurity concentrations and under different pressure and temperature conditions (e.g. Reference Fujita, Matsuoka, Ishida, Matsuoka, Mae and HondohFujita and others, 2000; Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others 2007). Then, using a known temperature profile measured at a drilling site, ice absorption can be evaluated along the ice-core profile.
The absorption loss rate can also be calculated starting from experimental data, using ice-core measurements from drilling projects in both Antarctica and Greenland. In these cases, the availability of a known temperature profile makes it possible to scale the measured calibrated DEP along the ice core. Figure 1 shows an example with the temperature and the corrected DEP profiles from values measured at Dome C, as part of EPICA (EPICA Community Members, 2004; Reference Wolff, Barnes and MulvaneyWolff and others 2004).

Fig. 1. Corrected ice conductivity (red line) and temperature (blue line) at EPICA drilling site.
At the Dome C site the conductivity value was measured at a temperature of –20 ± 2°C, scaled to a standard temperature of 258 K (–15°C; Reference Stauffer and WolffStauffer and others, 2004) using the Arrhenius model (Reference Corr, Moore and NichollsCorr and others, 1993; Reference Paden, Allen, Gogineni, Jezek, Jensen and LarsenPaden and others 2005; Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others 2007). In the same way the ice-core conductivity profile can be corrected for the temperature of the ice along the profile:

where R = 8.314472 J K−1 mol−1 is the gas constant and E = 0.22 eV is the activation energy (Reference KulessaKulessa, 2007). The conductivity profile (σ 258) is known for a temperature of 258 K, r i is the ice thickness, and T(r i) is the ice-core temperature profile. The smoothed value of ice conductivity at Dome C, calculated along an ice core 3165 m long, ranges from 3 to 13 µs m−1 (ignoring the firn layer), making it possible to consider the ice a relatively homogeneous medium.
In the assessment of the ice absorption rate using Eqn (1), dielectric permittivity was calculated using the relation σ′ = 3.1884 + (9.1 × 10–4 T) (temperature T in °C) (Mätzler and Wegmüller, 1987). The influence of temperature on dielectric permittivity and consequently on the EM ice absorption was evaluated in the temperature range as recorded at Dome C and, in any case, was <0.2 dB km−1. Figure 2 (red line) reports the absorption rate using Eqn (1), calculated on the basis of the conductivity and temperature profile from the EPICA ice-core dataset. In the plot, the absorption rate varies abruptly in the first 400 m. In this range the first 100 m are influenced by the presence of firn, while below close-off the remaining part is influenced by the changes in density, dust and grain size as shown in EPICA Community Members (2004). Deeper, two different steps are clearly visible: one at –3.6 dB km−1 ranging from 400 to 1560 m, and a second ranging from 1560 to 2500 m with an absorption rate that increases in magnitude to about –7 dB km−1. Finally, an irregular linear trend is visible at depths below 2500 m. These steps are probably linked to the different ice acidity variation due to volcanic catastrophic events. The average value of the ice absorption rate calculated in the first step (0–1560 m) is 3.4 ± 0.9 dB km−1, between 0 and 2600 m (two steps) it is –5.0 ± 2.4 dB km−1, while on the complete ice column it is –11 ± 3 dB km−1. This last value is affected by rapid variations in conductivity in the bottom portion of the ice-core profile.
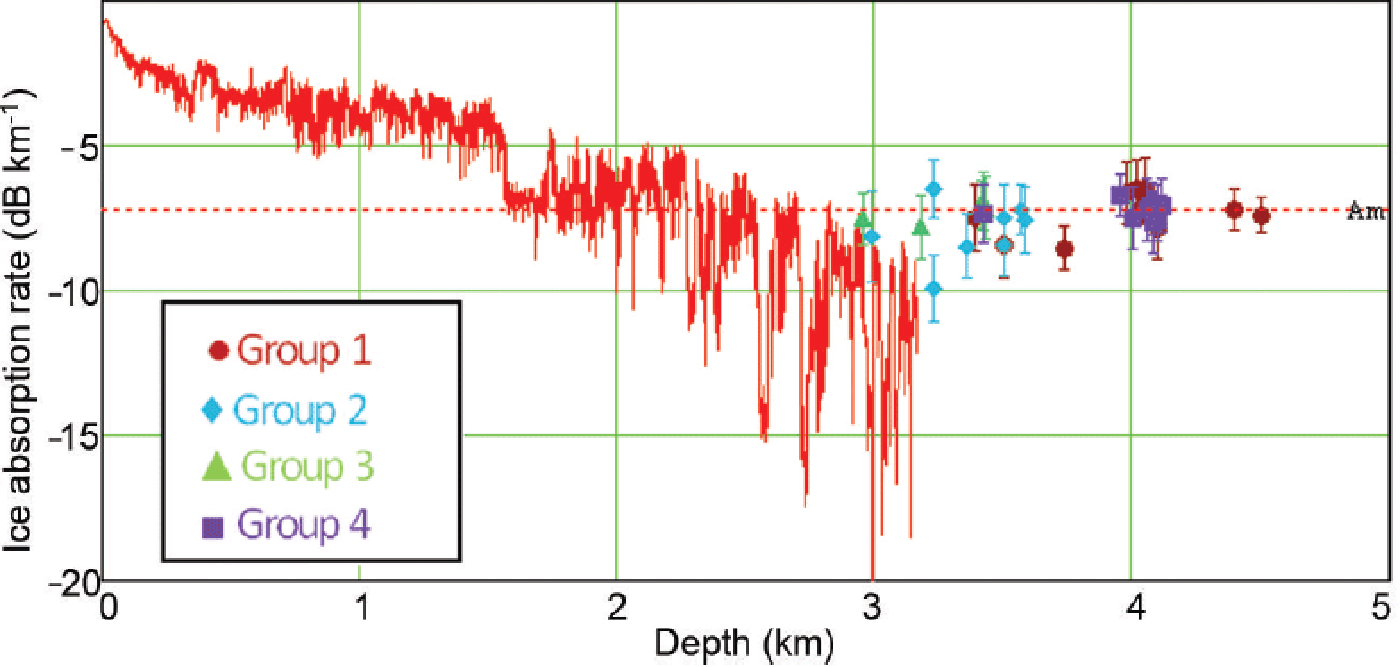
Fig. 2. Ice absorption rate at EPICA drilling site (red line) compared with those calculated by RES measurements over grouped subglacial lakes (Fig. 3).
Interface Between Reflecting Surfaces
To distinguish the different physical properties of reflecting surfaces, reference is made to homogeneous horizontal surfaces.
Table 1 (Reference DanielsDaniels, 1996; Reference Fujita, Matsuoka, Ishida, Matsuoka, Mae and HondohFujita and others, 2000; Reference Bianchi, Forieri and TabaccoBianchi and others, 2004) lists different media with related symbols, real and imaginary parts of the complex dielectric permittivity σr = σ′ − jσ″ (at a frequency of 60 MHz), conductivity and the range of considered values. The Fresnel reflectivity equation has a coefficient ρ at a separation surface between two media 1 and 2 (in the case of vertical incidence):
Table 1. Complex permittivity and conductivity

Power loss due to reflection R is equal to |ρ| 2, while power loss due to transmission is T = 1 – R (Reference Ulaby, Moore and FungUlaby and others, 1981).
Table 2 summarizes the power losses due to the reflection (R) or transmission (T) coefficients at the relative interfaces. The power loss calculated as in Reference Bogorodsky, Bentley and GudmandsenBogorodsky and others (1985) is negative and must be added to the incident power (dBm). The values and their errors are calculated considering the variability ranges reported in Table 1.
Table 2. Transmission and reflection variability ranges for several interfaces

In the case of a coherent flat reflector the radar equation, neglecting noise and scattering due to inhomogeneities and multiple reflections between layers, can be written as

where p t and p r are the transmitted and received power, G a is the antenna gain, λ is the RES signal wavelength, r is the range from transmitting antenna, and l p contains all the loss terms: geometrical spreading, ice absorption, losses due to the transmission and reflection coefficients T and R at the different interfaces (air, ice, ground, water, etc.) (Reference SkolnikSkolnik 1990; Reference Peters, Blankenship and MorsePeters and others 2005). The geometrical spreading l G can easily be evaluated, knowing the time delay of the echoes (distances), as

where r a and r i indicate the range in air (airplane altitude) and in ice (thickness of the ice). The term l G also contains the gain of the refractive effect when the wave propagates into the ice, characterized by the refractive index n = 1.79. The loss terms T and R, which define the reflecting EM properties at the various interfaces along the propagation path, are reported in Table 2.
From Eqn (4) the reflected power from the air/ice interface (ice surface) P ai can be written expressing signal power in dBm (using capital letters) as
where R ai is the power loss due to reflection at the air/ice interface and L Ga is related to the geometrical loss in air (l G at r i = 0).
Following the same procedure, reflected power from the ice/water surface P iw can be written as
where R iw represents the attenuation of the signal power reflected from the ice/water interface that, in this analysis, is the reflection from a subglacial lake at ice depth r i. The EM ice absorption L i includes all the glacial power losses due to variation in density, homogeneity and temperature of the ice. Hereafter the transmission coefficient of the internal layers is ignored and considered approximately zero (Reference MacGregor, Winebrenner, Conway, Matsuoka, Mayewski and ClowMacGregor and others, 2007; Reference Zirizzotti, Cafarella and UrbiniZirizzotti and others, 2012). All the terms P iw, 2L i and L Gr depend on ice depth r i.
Comparing Eqns (7) and (6), the loss term L i can be assessed for generic signals reflected from the ice/water interface (subglacial lake in this case) at depth r i and from the ice surface:
It is worth noting here that the difference between the terms P iw(r i) and P ai for bottom and surface reflection levels is a sort of normalization of the received signals that enables comparison of radar traces from different campaigns with different transmitted signal levels. Moreover, this procedure allows us to evaluate only the difference between L Ga and L Gr(r i) which does not depend on antenna gains, with a simplification in the analysis of the radar data. Furthermore the carrier frequency used does not affect the EM ice absorption for frequencies below 300 MHz (Reference Fujita, Matsuoka, Ishida, Matsuoka, Mae and HondohFujita and others, 2000).
Res Measurements Over Subglacial Lakes
During several Italian Antarctic RES campaigns (INGV, 2014), from 1995 to 2013, a large number of subglacial lakes were identified from analysis of the acquired radargrams (Reference Cafarella, Urbini, Bianchi, Zirizzotti, Tabacco and ForieriCafarella and others, 2006) and added to the international subglacial lakes catalogue. The Dome C area was chosen as an ideal location because of its abundance of subglacial lakes and the presence of the EPICA ice core. For this analysis, 35 subglacial lakes were selected, distributed 360° around the ice-core site and located at different depths in the ice. Figure 3 reports their positions on a bedrock map (Antarctic Polar Stereographic Projection, datum WGS84), while the main characteristics (mission number, latitude and longitude coordinates and ice thickness) are reported in Table 3. Lakes have been grouped in four different zones in the Concordia area to analyze different ice properties in different zones. The analyzed radar measurements were collected during different Antarctic campaigns using several different RES systems, with different transmitted peak powers (2–4 kW), and different pulse lengths (100 ns to 1 µs) at the same carrier frequency of 60 MHz (Reference Zirizzotti, Baskarades, Bianchi, Sciacca, Tabacco and ZuccherettiZirizzotti and others, 2008).

Fig. 3. Position of grouped subglacial lakes chosen for the analysis on a bedrock elevation map. Symbols indicate different ice absorption rate ranges (see legend).
Table 3. Subglacial lake measurements

In Table 3 the lakes are numbered according to mission number, latitude and longitude coordinates and ice thickness. The average ice absorptions were calculated over the lake extension using Eqn (8), with the transmission and reflection attenuation values reported in Table 2.
Absorption can be defined as
where Ā(r i) is the averaged absorption rate (dB km−1) calculated along the lake extensions. Using Eqns (8) and (9), the term A can be evaluated from lake RES profiles and it can be compared to the absorption rate A resulting from the ice-core measurements using Eqn (1). Figure 2 reports the calculated values of the average ice absorption rate Ā(r i) obtained from Eqn (9) using the L i and r i values (Table 3) plotted together with those calculated using the EPICA measurements (colored points and red line respectively). The absorption rate has been evaluated as the ratio between ice absorption and depths. The error in the absorption rate has been evaluated using the error propagation formula introducing the ice absorption errors and measured depth errors (depending on transmitted pulse length used). The absorption error has been evaluated as the sum of errors of Eqn (8) for each lake. The errors ΔR ai = 0.5 dB, ΔT ai = 0.5 dB and ΔR iw = 0.4 dB have been overestimated using 10% of the values, while the term Δ(LG a – LG r(r i)) is calculated with the propagation error formula in dB. The reflected powers P iw, P ai and their relative errors have been evaluated as mean power and standard deviation of the signal amplitude collected over the lake extensions.
The analyzed data profiles are located at different depths ranging from 2958 m (at it17; Fig. 3) to 4502 m (at it7; Fig. 3). Consequently, since the depth of the selected subglacial lakes ranges from 2960 to 4500 m, direct comparison between EPICA and RES ice absorption rate values is not possible.
The RES-based ice absorption rate values calculated from these different depths (over an area of ~16 000 km2 in Fig. 3) show an average value A m = –7.2 ± 1.4 dB km−1. This value agrees (within the errors) with the ice absorption rate obtained from EPICA measurements averaged over the range 0–2600 m, and is close to the value calculated in the interval 1560–2500 m (about –7.0 dB km−1, visible in Fig. 2). This value also agrees with the average absorption rate calculated from bedrock reflectivity over a smaller area (150 km × 50 km) around the EPICA drilling site as reported in Zirizzotti and others (2010, Reference Zirizzotti, Cafarella and Urbini2012). However, here the radar measurements of the ice absorption rate are relatively constant and they are independent of depth and of different zones in the area.
Attenuation of the radar signal across the Antarctic ice sheet using a thermomechanical model has been evaluated by Reference Matsuoka, Gregor and PattynMatsuoka and others (2012). The average value of ~10 ± 2 dB km−1 valid for the Dome C area is confirmed here. Reference Jacobel, Lapo, Stamp, Youngblood, Welch and BamberJacobel and others (2010) also made careful studies of radar attenuation in East Antarctica. Although they did not cover Dome C, they found an absorption rate of 8.6 ± 0.1 dB km−1.
For the first time, the results described in this paper take advantage of radar measurements over lakes where reflectivity (–3.5 dB) could be considered and used as a constraint in the analyzed area. Consequently the averaged value of A m (–7.2 dB km−1) could be used as a reference value for the ice absorption rate in the area over subglacial lakes, also considering that, in general, geothermal flux and accumulation rate can affect the temperature profile and, consequently, the absorption rate over a large area (Reference MatsuokaMatsuoka, 2011).
Conclusions
Over the past few years the discovery of numerous subglacial lakes has attracted scientific interest in the possible existence of water circulation between lakes and beneath the Antarctic ice sheet. For this purpose, analysis of the power of RES echoes has played a fundamental role in the characterization of basal physical conditions. The identification of subglacial lakes and/or dry–wet bedrock conditions is also extremely useful for formulating hypotheses and models of geothermal flux and ice column flow on the Antarctic plateau. While the recognition of subglacial lake surfaces is relatively easy in radargrams, understanding the ice/bedrock interface properties is usually more complicated. Signal amplitude in response to bedrock morphologies could depend on several different factors (e.g. a focusing effect, surface roughness, or changes in the EM properties of the ice column).
We have examined the latter factor and, in particular, the EM ice absorption rate obtained from RES profiles collected over subglacial lakes near Dome C, comparing the values with those obtained from EPICA ice-core drilling. The idea was to measure ice absorption starting from the radar equation with measurements taken over subglacial lakes, where the EM reflectivity value is known. The study included 35 catalogued subglacial lakes located at different depths (2960–4500 m) and arrayed ~360° around the ice-core site, in an aerial extension of ~16 000 km2. It was found that the calculated values fluctuated around an average value of –7.2 ± 1.4 dB km−1, independent of lake depth or location. This ice absorption rate value agrees with that obtained from the EPICA ice core valid in deeper ranges, and with the rate calculated over a smaller area around the drilling site (–7.5 ± 0.7 dB km−1). Moreover the lakes have been grouped in four different zones and no correlation has been found between ice absorption rate value and location. Consequently, this value can be used to estimate bedrock reflectivity when it is fundamental to identify the physical status of the bedrock. It might also help to improve confidence in wet– dry bedrock analysis relatively far from ice-core points, where changes in ice column absorption could mislead the interpretation of the received signal amplitude.
We conclude that ice absorption rate calculation over a district including lakes and using RES data could help to integrate the EM properties of the ice with the instrument responses, widening the significance of point data (i.e. ice cores) or providing a starting value where point data are not available.








