Introduction
The temporary storage and subsequent release of water at glacier margins can cause severe flooding in downstream areas and substantially impact glacier dynamics. Jokulhlaups commonly have peak discharges several orders of magnitude larger than precipitation-induced floods (Reference Clague and EvansClague and Evans, 1994). They alter valley bottoms, channel forms and riparian ecosystems, cause substantial erosion and aggradation (Reference Post and MayoPost and Mayo, 1971), and have caused severe damage to infrastructure up to 1200 km from their source (Reference Mason, Gunn and ToddMason and others, 1930). Consequently, they are the farthest reaching of all glacial hazards. In addition, jokulhlaups and pockets of subglacial water can substantially increase glacier velocity (Reference Fatland and LingleFatland and Lingle, 2002;Reference Anderson, Walder, Anderson, Trabant and FountainAnderson and others, 2005); some glaciers may not return to their pre-flood velocity for several years (Reference Magnusson, BjOrnsson, Rott and PalssonMagnusson and others, 2010).
Researchers have made substantial progress in remotely identifying and characterizing glacier-dammed lakes, including lakes at the base of ice sheets and ice caps (Reference Ridley, Cudlip and LaxonRidley and others, 1993;Reference Popov and MasolovPopov and Masolov, 2007;Reference Scharrer, Malservisi, Mayer, Munzer and SpielerScharrer and others, 2007;Reference Magnusson, BjOrnsson, Rott and PalssonMagnusson and others, 2010), subaerial lakes at the margins of glaciers (Reference Huggel, Kaab, Haeberli, Teysseire and PaulHuggel and others, 2002;Reference Bolch, Buchroithner, Peters, Baessler and BajracharyaBolch and others, 2008), and migrating pockets of subglacial water beneath alpine glaciers (Reference Fatland and LingleFatland and Lingle 2002; Reference Lingle and FatlandLingle and Fatland, 2003). However, alpine subglacial lakes may not be identified until they become subaerially exposed or release a jokulhlaup (Reference Post and MayoPost and Mayo, 1971; Reference Geertsema and ClagueGeertsema and Clague, 2005).
We use the term ‘glacier-dammed lake’ in reference to any lake that is dammed by glacier ice, irrespective of its position relative to the glacier (Reference Blachut, Ballantyne and HamiltonBlachut and Ballantyne, 1976). In contrast, a ‘subglacial lake’ is one that occurs primarily underneath a glacier, whether or not it is at atmospheric pressure (Reference Clague and EvansClague and Evans, 1994;Reference Tweed and RussellTweed and Russell, 1999). This primarily morphological definition contrasts with the usages of Reference SiegertSiegert (2000), who states that subglacial lakes are ‘discrete bodies of water that lie at the base of an ice sheet between ice and substrate’, and Reference HodgsonHodgson and others (2009), who further limit the term to lakes sealed off from, and presumably at higher pressure than, the atmosphere.
The objective of this study is to identify and characterize alpine subglacial lakes dammed by Brady Glacier, Alaska, USA, using interferometric synthetic aperture radar (InSAR). Specifically our goals are to: (1) confirm the existence of suspected subglacial lakes;(2) calculate the vertical displacement of the glacier over the lakes;(3) calculate the volume of water moving into or out of the subglacial lake system; and (4) characterize how these subglacial lakes affect Brady Glacier dynamics. We discuss how the knowledge we have gained can be applied in this and other glacierized areas around the world to minimize hazards posed by alpine subglacial lakes. Early identification and characterization may provide years or decades of warning of future jökulhlaups.
Study Area
Brady Glacier is located in the Fairweather Range of the Saint Elias Mountains in Glacier Bay National Park, 125 km west of Juneau, Alaska (Fig. 1). It is 51 km long and has an area of 590 km2. The glacier has an accumulation area ratio of 0.65, with an equilibrium-line altitude (ELA) of 610 m a.s.l. (Reference ViensViens, 1995). Brady Glacier terminates on its outwash plain approximately 10ma.s.l.;several of its smaller lobes terminate in secondary valleys trending east or west. Peaks up to 3467 m a.s.l. to the northwest supply most of the ice to the glacier. The glacier has deepened the north-northwest trending fault-controlled valley in which it lies far below sea level. Ice-penetrating radar measurements near the main axis of Brady Glacier indicate that the bed is at least 200 m below sea level (Reference Barnes and WattsBarnes and Watts, 1977). This valley is 64 km long and extends from Taylor Bay to the south to near the north end of Glacier Bay. Approximately two-thirds of the ice in this valley flows south-southeast towards Taylor Bay as Brady Glacier and one-third flows north-northwest into Lamplugh and Reid Glaciers (Reference BengtsonBengtson, 1962;Reference DerksenDerksen, 1976). The divide between south- and north-flowing ice lies at approximately 820ma.s.l. based on the 2000 Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM).

Fig. 1. False-colour Landsat image of Brady Glacier, southeast Alaska. Topographic contours derived from 2000 SRTM DEM (50m contour interval). Large lakes dammed by Brady Glacier numbered 1–10. Lakes discussed in text: (1) Divide Lake; (2) Hinge Lake; (3) Saddle Lake. (4) Abyss Lake; and (5) Oscar Lake.
The climate at Brady Glacier is cool and moist, typical of the maritime climate throughout southeast Alaska. The strong Aleutian low-pressure system that typically lies offshore in the Gulf of Alaska dominates the climate. This low-pressure system generates frequent storms that deliver >280 cm w.e. of average annual precipitation. Snow is common at sea level from late October until early April (Reference DerksenDerksen, 1976).
The history of Brady Glacier is broadly similar to that of other glaciers in the region, but there are a few notable differences. Most glaciers in the region reached their Little Ice Age maximum extents in the periods 1540-1710 and 1810-80, and are now retreating (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007; Reference Barclay, Wiles and CalkinBarclay and others, 2009). In contrast, Brady Glacier reached its current extent at about 1880 and its terminus has changed little since then. It was until relatively recently a tidewater glacier, which may explain its anomalous behaviour (Reference KlotzKlotz, 1899;Reference DerksenDerksen, 1976;Reference Molnia, Williams and FerrignoMolnia, 2008). The activity of tidewater glaciers is controlled more by calving dynamics than climate (Reference PostPost, 1975;Reference Motyka and BegetMotyka and Beget, 1996). Although Brady Glacier has maintained most of its length and area since the late 19th century, it has experienced substantial downwasting. Between 1948 and 2000, the glacier down- wasted at an average rate of 2-3 ma-1, which is above the regional average (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others 2007). Areas that downwasted the most are adjacent to glacier-dammed lakes; the lakes probably contributed to mass loss through calving. Field observations of the highest Little Ice Age trimline near North Trick Lake (lake 7, Fig. 1), at the southwest margin of the glacier, indicate that the total lowering of the glacier surface in that area is as much as 135 m, which supports the findings of Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others (2007).
We chose Brady Glacier because it presently dams at least ten large lakes that are in different stages of evolution: incipient, stable and non-draining, periodically draining, and extinct. This allowed us to examine how the lakes have evolved through time. Six of the lakes are subaerial;the other four are primarily subglacial, with >50% of their areas beneath glacier ice. We estimated the sub-ice extents of the four subglacial lakes from their floating ice ramps, the presence of open water around significant areas of flat or low- gradient glacier ice, and distinctive crevasses produced by filling and draining of the lakes. We measured water depths of up to 140 m along the margin of Oscar Lake (lake 5, Fig. 1).
In this paper, we focus on three previously unidentified subglacial lakes in dead-end valleys on the northeast side of Brady Glacier, which we informally name Divide Lake, Hinge Lake and Saddle Lake (Fig. 2). Other researchers have noted that Brady Glacier flows into these dead-end valleys, but did not identify the lakes (Reference BengtsonBengtson, 1962). Only small areas of water are exposed along the glacier margin. Divide Lake at 600m a.s.l. is the northernmost of the three lakes; it is approximately 1.5 km long and 0.5 km wide. It is near the Brady Glacier ice divide below Divide Peak and underlies a northeast-trending distributary lobe that is confluent with a small southwest-flowing tributary glacier (Fig. 2). Hinge Lake at 450ma.s.l. is the middle of the three lakes and is 4.2 km long and 1.3km wide. It has a distinctive hinge-like crevasse that runs along the axis of a northeast-trending distributary lobe. Small areas along the margins of this lobe are open water. Saddle Lake, also at 450ma.s.l., is the southernmost of the three lakes, is ˜2.0 km long and 1.6 km wide and has a saddle-shaped perimeter. The lake underlies a distributary lobe that flows eastward before splaying into embayments to the northeast and southeast. The part of the lake in the southeast embayment underlies the distributary lobe and a small tributary glacier flowing to the north.

Fig. 2. 1997 digital orthophoto of the study area with contours derived from 2000 SRTM DEM (25m contour interval).
Line-of-Sight Displacement
Datasets
Our InSAR measurements are based on four ascending and six descending European Remote-sensing Satellite-1/-2 (ERS- 1/-2) image pairs of Brady Glacier provided by the European Space Agency (Table 1) and the SRTM DEM. The ERS image pairs were acquired in 1995 and 1996 and provide short spatial and temporal baselines. All tandem images were captured 24hours apart and have a spatial resolution of 20 m. We chose this dataset primarily because short temporal baselines are necessary to avoid decorrelation of the images, which is a common problem on temperate glaciers. The SRTM DEM, acquired in 2000, has a spatial resolution of 30 m.
Table 1. ERS images used in this study

Interferogram processing
We created ten interferograms from the 20 SAR images using standard InSAR processing techniques (http://www.gamma-rs.ch/uploads/media/gamma_soft_09.pdf). Two interferograms were unusable because of poor coherence. Precipitation recorded at the Elfin Cove meteorological station 23 km southwest of Brady Glacier (http://www.ndbc.noaa.gov/station_history.php?station=cspa2) leads us to suspect that precipitation in the study area caused the decorrelation. The remaining eight interferograms are of good quality and show recurring ‘bull's-eye patterns' at the location of each of the hypothesized subglacial lakes. Figure 3a shows an example of substantial displacement from 29 to 30 September 1995 over all three subglacial lakes. Figure 3b shows much less displacement from 23 to 24 March 1996 over the three lakes; Hinge Lake experienced negligible displacement during this period.

Fig. 3. Interferograms for (a) 29_30 September 1995 showing substantial displacement over all three subglacial lakes and (b) 23_24 March 1996 showing much less displacement over the same area. For C-band ERS, with a wavelength of 5.6 cm, one fringe corresponds to a difference in LOS ground displacement of 2.8 cm. Thus, in (a) the LOS displacement at the centre of Hinge Lake over the 24 hour period is 10 cm.
In the case of two of the eight usable interferograms, we encountered localized but substantial problems in unwrapping the fringe colour ramp pattern due to areas of low coherence and fringe aliasing (fringes become too dense to identify each one unambiguously). Because all perpendicular baselines are relatively small, only a change in surface scattering at subresolution scale can explain low coherence. This change in scattering was likely due to temporal decorrelation caused by precipitation or melt. Unfortunately, the two problematic interferograms are among the most interesting of the ten. One of them shows the largest observed displacement over the three lakes and the other shows substantial displacement associated with all three lakes. The presence of discontinuous fringes prevented the use of traditional unwrapping routines. To address this problem, we developed a method to improve the unwrapping.
Interactive unwrapping
Although we could not successfully unwrap the fringe colour ramp patterns in all examples with standard techniques, we were able to identify the problematic areas through visual analysis (Fig. 4a) and correct them using an iterative process. Wrapped 32-bit interferogram files were exported to 8-bit bitmap files, and individual pixels were modified manually using a standard raster graphics program so that areas of low coherence or high aliasing were clarified. The clarified 8-bit image was cast back to a 32-bit file, masked to remove problematic zones outside the area of interest, and unwrapped with a standard algorithm (Reference CostantiniCostantini, 1998). This result was then used to demodulate the original image. Figure 4b shows the original image unwrapped using this method. The new unwrapping result has an accuracy of better than one fringe in the corrected areas because we used a conservative approach during the clarification process and masked areas where this level of accuracy was not attainable.

Fig. 4. (a) Unsuccessfully unwrapped displacement map of Hinge Lake derived using standard techniques (note discontinuity in colour pattern) and (b) successfully unwrapped displacement map derived using an iterative unwrapping technique.
Application of this unwrapping technique is limited. It can resolve only localized unwrapping problems, and substantial user input during the clarification process precludes its application to larger regions or areas with very low coherence or high aliasing. However, the technique solved localized unwrapping problems caused by mild aliasing and temporal decorrelation.
Isolating Horizontal and Vertical Displacement
Two-dimensional displacement maps
Displacements in single-track interferograms are line of sight (LOS), so they require additional steps to separate the horizontal and vertical components. Reference Joughin, Kwok and FahnestockJoughin and others (1998) introduced a technique to discriminate horizontal and vertical displacements that utilizes two interferograms, one ascending and one descending. Two conditions must be met to apply this technique successfully: (1) there must be a third constraint on displacement complementing the two interferometric observations;and (2) glacier motion over the entire interferometric observation period must be constant, i.e. the two interferograms must represent the same rate and area of displacement despite being acquired at different times. Constraints have been developed to meet the first condition, such as assuming surface-parallel flow (Reference Joughin, Kwok and FahnestockJoughin and others, 1998), applying mass conservation principles (Reference Reeh, Mohr, Madsen, Oerter and GundestrupReeh and others, 2003) or using an ice-flow direction map (Reference Rabus and FatlandRabus and Lang, 2000;Reference Fatland, Lingle and TrufferFatland and others, 2003).
We produced two-dimensional displacement maps for our study area from pairs of near-concurrent (acquired within <1 day) ascending and descending tandem interferograms and an inferred ice-flow map. Although we were able to meet the first condition by deriving a reliable ice-flow map from ubiquitous flow features in the study area, results with unreasonably large horizontal displacements showed that the second condition was not met: vertical displacement rates over the lakes varied considerably over a single day, precluding use of an averaged 24hour vertical displacement rate.
One-dimensional displacement maps
Fortunately, we were able to calculate one-dimensional (1-D) (vertical) displacement using single interferograms because we can demonstrate that horizontal displacement is negligible. 1-D displacement maps offer definite advantages because they do not require displacement over the observation period to be constant and because we can obtain as many observations of vertical displacement as there are individual interferograms.
Our argument for negligible horizontal displacement over the subglacial lakes is supported by several lines of evidence. Although unconstrained floating margins can move by lateral spreading and gravitationally driven ice flow, each of the three lobes in the study area flows into a dead-end valley bordered by steep rock walls that do not allow the floating margin to spread. Furthermore, the glacier flows into the valleys very slowly because floating ice must ablate or melt and drain before the glacier can replace it. The vertical displacement patterns in the interferograms closely correlate with distinctive crevasses over the lakes (Fig. 5). These patterns are consistent and discernible in aerial photographs from 1948 to the present and over four seasons of fieldwork observations. The crevasses converge towards the areas of maximum vertical displacement and therefore are probably caused by repeated inflation and subsidence, not by horizontal displacement. ERS is more sensitive to vertical than horizontal displacement because of its steep average look angle of 23.5° from vertical (Reference Joughin, Kwok and FahnestockJoughin and others, 1998). Most importantly, regardless of the track angle, subsidence will always create a fringe colour ramp pattern that indicates motion away from the sensor. Depending on the track angle, horizontal displacement will create a pattern that indicates displacement either towards or away from the sensor. The pattern of the lakes in all the interferograms in our study shows that all displacement associated with the lakes is away from the sensor, consistent with subsidence. Therefore, we assume that all displacements associated with the lakes are vertical. We calculated total vertical displacement from the edge of the lake, where displacement is zero, to the area of maximum displacement. Results are shown in Table 2.

Fig. 5. Correlation of (a) crevasses seen in 1997 aerial photograph with (b) LOS displacement in the interferograms.
Table 2. Maximum subsidence (cm) at Divide, Hinge and Saddle Lakes in 24 hours

Error analysis
We estimated the total error, ϕ, by summing the errors associated with the individual components used to calculate the interferometric signal. The interferometric signal is the result of orbit geometry, o, surface topography, t, atmospheric changes, a, sensor noise, n, and vertical (dv) and horizontal (dh) surface displacement:
Errors associated with ERS orbit geometry are small (Reference Mohr and MadsenMohr and Madsen, 2001);we ignored them in this study. Errors associated with surface topography are the result of inaccuracies in the DEM and changes in the surface elevation of the ice between acquisition of the ERS images and the images used to produce the DEM. Spikes and wells (single pixel errors) in the DEM were removed (http://seamless.usgs.gov/faq/srtm_faq.php#three). Sizeable voids remained in high-relief bedrock areas but were not present over the glacier. Relative vertical error for the DEM was <6 m, of which about one-third was systematic and the remainder random (Reference Rabus, Eineder, Roth and BamlerRabus and others, 2003). We were unable to measure elevation changes directly between the time the ERS images were acquired in 1995/96 and the time the images for the DEM were acquired in 2000. Based on thinning rates derived from laser altimetry (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007), we estimated the elevation change to be <8m: <0.08 fringes for a 100 m baseline and <0.16 fringes for a 200m baseline (Reference Rabus and FatlandRabus and Fatland, 2000). Thus, we conservatively estimated a maximum of 15 m total elevation error, yielding an error of 0.15 fringes for a 100 m baseline and 0.3 fringes for a 200m baseline. Under extreme circumstances, atmospheric changes can cause errors of 1 fringe or larger. Most atmospheric distortions, however, occur over large areas (Reference Rabus and FatlandRabus and Fatland, 2000). Because we calibrated displacement over the lakes separately and each lake is relatively small, we assume that this source of error is negligible. Noise due to errors associated with sensor noise and temporal decorrelation is spatially random and cancels when ice volume is integrated spatially. The remaining error is the neglected horizontal surface displacement, d h.
If we assume d h = 0, the total error is
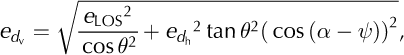
where α, ψ and θ are, respectively, the horizontal flow angle, the satellite track angle and the incidence angle, θ23.5°. Assuming a maximum horizontal ice displacement error over the lakes of 1 cm d-1 and evaluating LOS error, e LOS, for a 200 m baseline and extreme values of α and ψ Equation (2) gives a maximum error of ≤0.3 cm of vertical displacement over the lakes.
Displacement-Volume Calculation
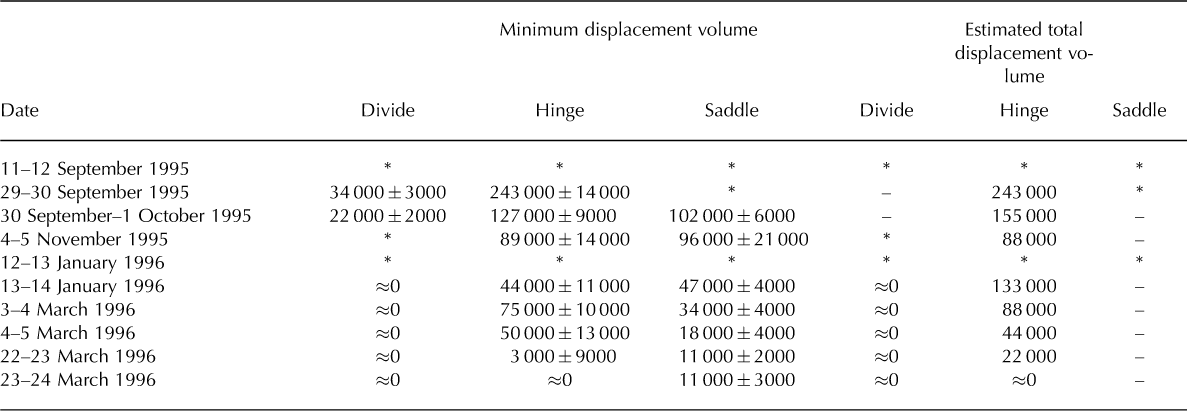
Using GIS, we calculated the maximum vertical displacement of all pixels over the subglacial lakes and, from those values, the volume of water displaced in discrete 24 hour intervals. We were unable to determine vertical displacements for all pixels and therefore accurate displacement volumes in all interferograms because of substantial areas of poor coherence, fringe aliasing and radar layover and shadow. However, we were able to determine the minimum displacement volumes for most of the lakes through the period of data acquisition (Table 3). We calculated the volume error by multiplying the systematic error (≤0.3 cm) by the masked lake area.
Table 3. Minimum and estimated total volume (m3) of water displaced from Divide, Hinge and Saddle lakes in 24 hours
We estimated total displacement volumes for lakes that had to be masked due to poor coherence, fringe aliasing and radar layover and shadow. We compared interferograms, one with nearly complete coverage and those with substantial masked areas, to calculate the estimated total displacement volume using
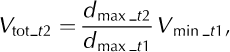
where V tot_t2 is the lake of interest’s estimated total displacement volume, d max_t2 is the lake of interest’s maximum vertical displacement, d max_t1 is the nearly complete lake’s maximum vertical displacement and V min_t1 is the nearly complete lake’s minimum displacement volume. In some cases, especially at Saddle Lake, complex and temporally inconsistent fringe patterns precluded this approach (Table 3).
Discussion
Subglacial hydrology
All coherent interferograms used in this study show bull’s-eye patterns that indicate subsidence of the glacier surface over the lakes. Reference Joughin, Winebrenner, Fahnestock, Kwok and KrabillJoughin and others (1996) also noted bull’s-eye patterns in interferograms of a Greenland outlet glacier, but there the patterns were persistent, occurred as conjugate pairs and resulted from downstream ice flow over subglacial topography. In the case of Brady Glacier, the bull’s-eye patterns are neither conjugate pairs nor persistently recurring. Like Reference Fatland and LingleFatland and Lingle (2002), we interpret this subsidence to result from draining of water at the base of Brady Glacier. Previously, the glacier had separated from its bed when the water reached a sufficient depth to float the ice. Reference Fatland and LingleFatland and Lingle (2002) concluded that the bull’s-eye patterns of Bering Glacier were distorted due to downstream ice flow. The bull’s-eye patterns at Brady Glacier are not located along the axis of flow and are not elongated because of downstream ice flow, but rather because of subglacial bedrock topography. The bull’s-eye patterns associated with Divide and Hinge Lakes are elongated because the basins in which they lie are elongated and therefore limit the areal extent of the subsidence (Fig. 3a). During drainage, the previously level ice surface subsides unevenly onto the glacier bed. Deeper depressions in the northern and southern embayments of Saddle Lake allow for larger amounts of subsidence in those areas (Fig. 3b). The depressions likely were excavated by cirque glaciers in the past;both are still present, but only one remains connected (Fig. 2). As a result, these areas continue to subside after the main floating margin has become grounded, which causes the magnitude and shape of the bull’s-eyes in the interferograms to change over time. Conversely, during lake inflation, the ice cover in the deepest areas of the lake likely begins to rise first. We attempted to determine ice thicknesses and subglacial topography in the lake basins using ice-penetrating radar, but most of the glacier bed was several hundred metres thick and beyond the range of our equipment.
We calculated the volume change per unit area of the three lakes through time. The lakes experienced their highest discharges (Table 2) and greatest volume changes per unit area in late September: 0.033, 0.053 and 0.050 m3 m-2 for Divide, Hinge and Saddle Lakes, respectively. The value for Divide Lake may be lower than those for the other two lakes because Divide Lake is 150 m higher and near the ELA and therefore has less meltwater available for draining.
Glacier-dammed lakes typically fill in the spring and early summer and drain in late summer and early autumn, although some lakes may drain at any time of the year (Reference LiestølLiestøl, 1956;Reference Post and MayoPost and Mayo, 1971). The subglacial lakes in this study exhibit this seasonality, with the largest discharges in early autumn, although discharge continued through the winter at lower rates (Table 2). Generally, the times of highest discharge are also the times of highest meltwater availability. No ERS-1/-2 tandem data are available from late March to early September to determine when the lakes fill to their highest levels, although we assume lake levels are highest when melt is greatest during late spring to late summer. Limited field observations showed that the floating margins over the lakes were at their maximum height in early to mid-August of each year from 2005 to 2007. During fieldwork in early April 2007, we observed the floating margins on all three lakes to be at low levels, with Saddle Lake several tens of metres below its full-pool level based on elevations of icebergs at its margins. These icebergs, which previously were floating at the margins of the subglacial lake, were stranded as the lake drained. Assuming that similar processes were operating in 1995/96 and 2007, we can compare the 2007 field observations with the 1995/96 InSAR results to test whether the measured surface displacements are consistent with the lake level lowerings inferred from the stranded icebergs. If we conservatively assume that the level of Saddle Lake fell by 20cmd-1 in September and October, 10cmd-1 in November and December and 5 cm d-1 in January through March (Table 2), the lake would drop by more than 22 m. However, we know that the lake fell by as much as 30 cm d-1 in November. As a result, we conclude that the processes active in 1995/96 were still active in 2007 and can explain the several tens of metres of difference between the low and high lake levels that we observed in the field. Based on these field observations, we estimate total annual vertical displacements of 25 m for Divide Lake, 30 m for Hinge Lake and 35 m for Saddle Lake.
We estimate the total minimum volume displacement from the three lakes to be approximately 1 000000± 129000m3 for the eight full days of the 177 day period for which we have measurements. We emphasize, however, that this estimate is conservative because we were unable to quantify some areas due to poor coherence, fringe aliasing and radar layover and shadow. If we assume that the eight full days of measurement (1 × 106 m3) are representative of discharge through the longer observation period (177 days), about 22x106 m3 of water discharged from the subglacial lake system. Some of this water is derived from melt and precipitation in the lake basins, but without mass balance or subglacial melt measurements we cannot determine their local contribution to lake level. It is likely that some of the water that accumulates in the lakes is derived from up-glacier positions and is brought to the lakes along the glacier margin or via subglacial conduits (see below). Although the volume of water displaced from these lakes is substantial, it is unclear whether the discharge significantly affects the motion of a glacier as large as Brady Glacier.
We considered the question of whether subglacial lake drainage at Brady Glacier is sudden and catastrophic or continuous and non-catastrophic. We cannot definitively answer this question because coherent radar data are temporally discrete and discontinuous. However, measured drainage from Divide and Hinge Lakes slowed markedly from the end of September to the beginning of October (Table 2), consistent with catastrophic drainage. Many jokulhlaup hydrographs increase exponentially to a peak, then fall very rapidly (Reference Walder and CostaWalder and Costa, 1996). However, the highest measured discharges are in early September and the lakes continued to drain, albeit at lower rates, through the period of the last interferogram in late March. This overall trend supports a hypothesis of slower, more continuous drainage.
The lakes drain through subglacial or englacial conduits or marginal channels. However, determining the type of conduit or channel functioning here is difficult. We did not find any surface expressions of conduits or marginal channels in the interferograms, aerial photographs or field. There are no gauging stations on any of Brady Glacier’s outlet streams. We cannot calculate the most likely drainage path without subglacial topographic data. We suspect, however, that the water drains down-gradient into Abyss Lake (Fig. 1). Analogous behaviour exists down-glacier where Abyss Lake drains subglacially into informally named Oscar Lake (Reference GroverGrover, 2003).
Early identification of glacier-dammed lakes
Early identification of glacier-dammed lakes is critical to minimizing the hazard of jcikulhlaups. Rapid changes in the cryosphere are leading to hazardous situations with few, if any, historical precedents (Reference Frey, Haeberli, Linsbauer, Huggel and PaulFrey and others, 2010). Early identification of future jcikulhlaups requires an understanding of the jokulhlaup cycle. Many glacier-dammed lakes go through a cycle of jokulhlaup activity as their dams weaken due to downwasting and retreat (Reference Clague and EvansClague and Evans, 1994). A critical threshold is reached when the glacier can no longer impound the lake and a cycle of jcikulhlaups begins. With continued downwasting or retreat, the frequency of jcikulhlaups may increase, but the magnitude decreases until eventually the water establishes a permanent outlet and jcikulhlaups cease.
The subglacial lakes described here will likely enlarge and become subaerial as Brady Glacier continues to downwaste and retreat. Portions of all three lakes already have subaerial exposure and these areas are likely to grow in the future. With continued glacier downwasting and retreat, they will likely enter the jokulhlaup cycle and begin to drain catastrophically. Reference Geertsema and ClagueGeertsema and Clague (2005) documented an example of this kind of evolution with Lake No Lake, which is dammed by Tulsequah Glacier in northwest British Columbia, Canada. Lake No Lake is not visible in 1948 aerial photographs, but a glacier ramp drops to a floating margin that covered a subglacial lake. This geometry is very similar to that of the lakes described in this study. By 1974, a sizeable subaerial lake had developed and it is still growing in area. In 1991 the lake began a cycle of jcikulhlaups. The volume of water discharged from Lake No Lake remains large, but, with continued glacier downwasting and retreat, the lake and its floods will decrease in volume (Reference Geertsema and ClagueGeertsema and Clague, 2005).
Brady Glacier’s Abyss Lake (Fig. 1) has undergone a similar transformation. On the International Boundary Commission’s topographic map of the study area, which is based on measurements taken in 1907, the area that is now Abyss Lake appears as a glacier ramp that drops to a floating margin (IBC, 1923). Aerial photographs taken in 1948 show Abyss as a large subaerial lake. Since that time, the subaerial part of Abyss has expanded. The lake has partially emptied most years since 1994, draining subglacially into Oscar Lake and over a bedrock sill into the Oscar Creek drainage, where the floodwaters caused widespread damage to the forests. The 1994 jokulhlaup, which caused the level of Abyss Lake to fall 77 m, released approximately 130×106 m3 of water and was the first discernible flood in that drainage for at least 80years based on dendrochrono- logical evidence (Reference GroverGrover, 2003). We conducted a bathymetry survey of Abyss Lake in 2006 and determined that when full to overflow, it is at least 270 m deep, very steepsided and contains >500 × 106 m3 of water. With continued glacier downwasting, jcikulhlaups from Abyss Lake eventually will drain subglacially to the Brady Glacier terminus, completely emptying the lake. Jcikulhlaups of this magnitude could erode the stabilizing outwash plain and return the glacier to a calving regime, which could have serious implications for the stability of the glacier. The subglacial lakes in this study will likely parallel Abyss Lake’s evolution from subglacial and relatively stable to subaerial with catastrophic outbursts. Abyss Lake and the subglacial lakes in this study illustrate how space can be used as a proxy for time in the evolution of glacier-dammed lakes.
Forecasting the evolution of the subglacial lakes reported in this paper is difficult because of the many complicating factors, such as uncertainties in future climate. However, if Brady Glacier continues to downwaste at a rate similar to that of the past 100years, Saddle and Hinge Lakes will likely begin to release jcikulhlaups within a few decades and Divide Lake will enter the jokulhlaup cycle perhaps a few decades later. We base this estimate on the evolutionary history of Abyss Lake and Lake No Lake, which have similar glacier geometries and hydrologic conditions.
Application of technique to other areas
The technique for identifying and characterizing subglacial lakes that we applied in this study can be used in other glacierized areas. For example, it could be used to verify a large subglacial lake in the Witches Cauldron, a tributary to Baird Glacier in southeast Alaska, which Reference Post and MayoPost and Mayo (1971) suggested could drain catastrophically. Reference Post and MayoPost and Mayo (1971) also identified a subglacial lake beneath Skilak Glacier near Seward, Alaska, based on a distinctive radial crevasse pattern on its surface. Jcikulhlaups from this lake have caused extensive damage to downstream infrastructure. We have identified several other large subglacial lakes in southeast Alaska and western British Columbia that have geometries similar to those found at Brady Glacier. Notable examples include the Dead Branch of Norris Glacier near Juneau, which has a conspicuous crevasse along its centre line, similar to Hinge Lake (Fig. 5), and an unnamed tributary of Patterson Glacier near Petersburg, Alaska. The successful application of this technique to other glacierized alpine areas would allow the identification and quantification of subglacial lakes before they began to release hazardous jokulhlaups. The rapid changes occurring in the cryosphere will likely lead to many new lakes forming beneath down- wasting alpine glaciers around the world (Reference Frey, Haeberli, Linsbauer, Huggel and PaulFrey and others, 2010). The number of such lakes may eventually decrease due to continuing glacier retreat and demise, but in the short term many new lakes will form and evolve in a warming climate. Because 1995/96 ERS-1/-2 tandem mission images are available for most alpine glaciers, our technique could be used to confirm suspected alpine subglacial lakes and to quantify their area and behaviour. Although more recent radar imagery with adequately short temporal baselines is limited, many new InSAR satellites are planned for the future that will extend the usefulness of the technique.
Summary
We developed a technique to isolate vertical displacements over dynamic alpine subglacial lakes using ERS-1/-2 imagery. We assumed, based on several lines of supporting evidence, that horizontal displacement over subglacial lakes in stagnant embayments is negligible. This assumption allowed us to quantify vertical displacement using single interferograms. We were able to determine maximum vertical displacement and displacement volumes for interferograms with good coherence and minimal aliasing. All interferograms in this study indicate that the lake surfaces are subsiding, but at different rates. Discharge rates are highest in late September, slow dramatically during winter and continue at lower rates through March.
Our technique can be applied to other glacierized areas. Imagery acquired during the ERS-1/-2 tandem mission and imagery provided by future InSAR sensors can be used in conjunction with this technique to identify and characterize alpine subglacial lakes in other glacierized areas. This technique allows researchers to locate subglacial lakes that may cause severe flooding in downstream areas and substantially impact glacier dynamics. Subglacial lakes may drain catastrophically years or decades from now, so our technique may allow time to mitigate the risk from this hazard.
Acknowledgements
This research was funded through a Canon National Parks Science Scholarship to D.M. Capps and a Natural Sciences and Engineering Research Council of Canada Discovery Grant to J.J. Clague. The European Space Agency provided ERS-1/-2 data. We thank MacDonald Dettwiler and Associates, specifically H. Zwick for project oversight and P. Ghuman for guidance in processing InSAR data, Glacier Bay National Park for maps, aerial photographs, local information, safety checks and lodging, Marmot Mountain Ltd for providing equipment that kept us safe and warm, G3 Genuine Guide Gear for backcountry ski equipment, D. Olson for flights to and from the glacier under challenging conditions and C. Larsen for data. We thank D. Fatland and N. Ross for their incisive and helpful reviews of drafts of the paper.










