Increasing contribution of grain boundary compliance to polycrystalline ice elasticity as temperature increases

Abstract

Measured elastic stiffnesses of ice polycrystals decrease with increasing temperature due to a decrease in grain boundary stiffness with increasing temperature. In this paper, we represent grain boundaries as imperfectly bonded interfaces, across which traction is continuous, but displacement may be discontinuous. We express the additional compliance due to grain boundaries in terms of a second-rank and a fourth-rank tensor, which quantify the effect on elastic wave velocities of the orientation distribution as well as the normal and shear compliances of the grain boundaries. Measurement of the elastic stiffnesses allows determination of the components of these tensors. Application of the method to resonant ultrasound spectroscopy measurements made on ice polycrystals enables determination of the ratio B_N/B_S of the normal to shear compliance of the grain boundaries, which are found to be more compliant in shear than in compression. The ratio B_N/B_S is small at low temperatures, but increases as temperature increases, implying that the normal compliance increases relative to the shear compliance as temperature increases.

NOTATION

a

radius of a pore represented as an oblate spheroid

A ^(r)

the area of the r-th grain boundary

B

grain boundary compliance tensor with components B _ij

B _N

normal compliance of a grain boundary

B _S

shear compliance of a grain boundary

c

half-thickness of a pore represented as an oblate spheroid

c/a

aspect ratio (thickness divided by lateral extent)

C

fourth-rank elastic stiffness tensor with components C _ijkl

C _ij

components of the fourth-rank elastic stiffness tensor in the two-index notation (Voigt, 1910; Nye, 1985)

k

wavenumber

K

bulk modulus

K ₀

bulk modulus of the sample when the ice crystals are fully bonded as occurs at low temperatures

K _r

permeability of the medium including the contribution of the grain boundaries

n

the unit normal (vector) to a grain boundary

$n_i^{(r)} $

the i-th component of the normal to the r-th grain boundary

S

fourth-rank elastic compliance tensor with components S _ijkl

$S_{ijkl}^0 $

components of the fourth-rank elastic compliance tensor that polycrystalline ice would have if the ice crystals formed a continuous framework

ΔS _ijkl

components of the fourth-rank excess compliance tensor that results from the presence of grain boundaries

t

traction vector

t _i

the i-th component of the traction vector

u

displacement vector

u _i

the i-th component of the displacement vector

[u]

difference in displacement between opposing sides of a grain boundary

[u _N]

component of the difference in displacement between opposing sides that is normal to a grain boundary

[u _S]

component of the difference in displacement between opposing sides that is parallel to a grain boundary

V

volume

V _P

compressional velocity; P-wave velocity

V _S

shear velocity; S-wave velocity

X ₁, X ₂, X ₃

reference set of Cartesian axes with X ₃ normal to a grain boundary

x ₁, x ₂, x ₃

reference set of Cartesian axes fixed in the sample

α _ij

components of the second-rank compliance tensor α representing the mechanical effect of the grain boundaries in polycrystalline ice

β _ijkl

components of the fourth-rank compliance tensor β representing the mechanical effect of the grain boundaries in polycrystalline ice

δ _ij

Kronecker delta with the property that δ _ij = 1 if i = j, and δ _ij = 0 if i ≠ j

η _f

fluid viscosity

κ _f

fluid bulk modulus

μ

shear modulus

μ ₀

shear modulus of the sample when the ice crystals are fully bonded as occurs at low temperatures

ν

Poisson's ratio

ρ

density

ω

angular frequency

INTRODUCTION

Grain boundaries in polycrystalline ice influence various mechanical phenomena such as creep, yield and fracture (Higashi, 1978). Grain boundaries may affect the use of elastic waves to investigate the properties of ice sheets and glaciers such as ultrasonic velocity measurements on cores (Bennett, 1968; Gow and Kohnen, 1979; Kohnen and Gow, 1979; Langway and others, 1988; Anandakrishnan and others, 1994), sonic logs (Bentley, 1972; Gusmeroli and others, 2012; Kluskiewicz and others, 2017) and seismic methods (Bentley, 1972; Bentley and Kohnen, 1976; Blankenship and Bentley, 1987; Horgan and others, 2008; Wittlinger and Farra, 2012; Picotti and others, 2015; Smith and others, 2017). Above −10°C, Duval and others (1983) report a large change in grain boundary mobility, which they suggest may be due to grain boundary melting that involves a zone with liquid-like structure at the grain boundaries. Such liquid-like water may exist at grain boundaries at temperatures as low as −30°C (Hobbs, 1974; Dash and others 1995; Vaughan and others, 2016). This may play a role in the mechanical behavior of ice sheets, since temperatures at the base may exceed the melting point even though near-surface temperatures are typically below −20°C (Iken and others, 1993; Engelhardt, 2004; Joughin and others, 2004; Cuffey and Paterson, 2010; Pattyn, 2010; Vaughan and others, 2016).

The purpose of this paper is to obtain information of the variation in the elastic compliance of grain boundaries in polycrystalline ice as a function of temperature from elastic wave measurements. For this, the measurements of Vaughan and others (2016) are used. These authors employ resonant ultrasound spectroscopy and ultrasonic transmission measurements to determine the temperature dependence of the elastic and anelastic properties of samples of polycrystalline ice with homogeneous texture and grain size <1 cm. Electron backscatter diffraction showed that the samples used had a close to random orientation distribution of ice crystals. Estimates of elastic anisotropy indicated a P-wave anisotropy of order 0.1%, so that the samples may be treated as elastically isotropic (Vaughan and others, 2016).

Resonant ultrasound spectroscopy measurements were performed on polycrystalline ice by Vaughan and others (2016) between −26°C and −5°C. Estimates of the compressional elastic stiffness C ₁₁, corresponding to the P-wave velocity $V_{\rm P} = \sqrt {C_{11}/\rho} $, where ρ is density, and shear stiffness C ₅₅, corresponding to the S-wave velocity $V_{\rm S} = \sqrt {C_{55}/\rho} $, obtained by Vaughan and others (2016) using these measurements, assuming the samples are isotropic, are shown in Figure 1. The elastic stiffnesses are seen to decrease with increasing temperature. However, the elastic stiffness C ₁₁ is more sensitive to temperature than the elastic stiffness coefficient C ₅₅, and Vaughan and others (2016) attribute this to liquid phases on ice grain boundaries associated with pre-melting conditions.

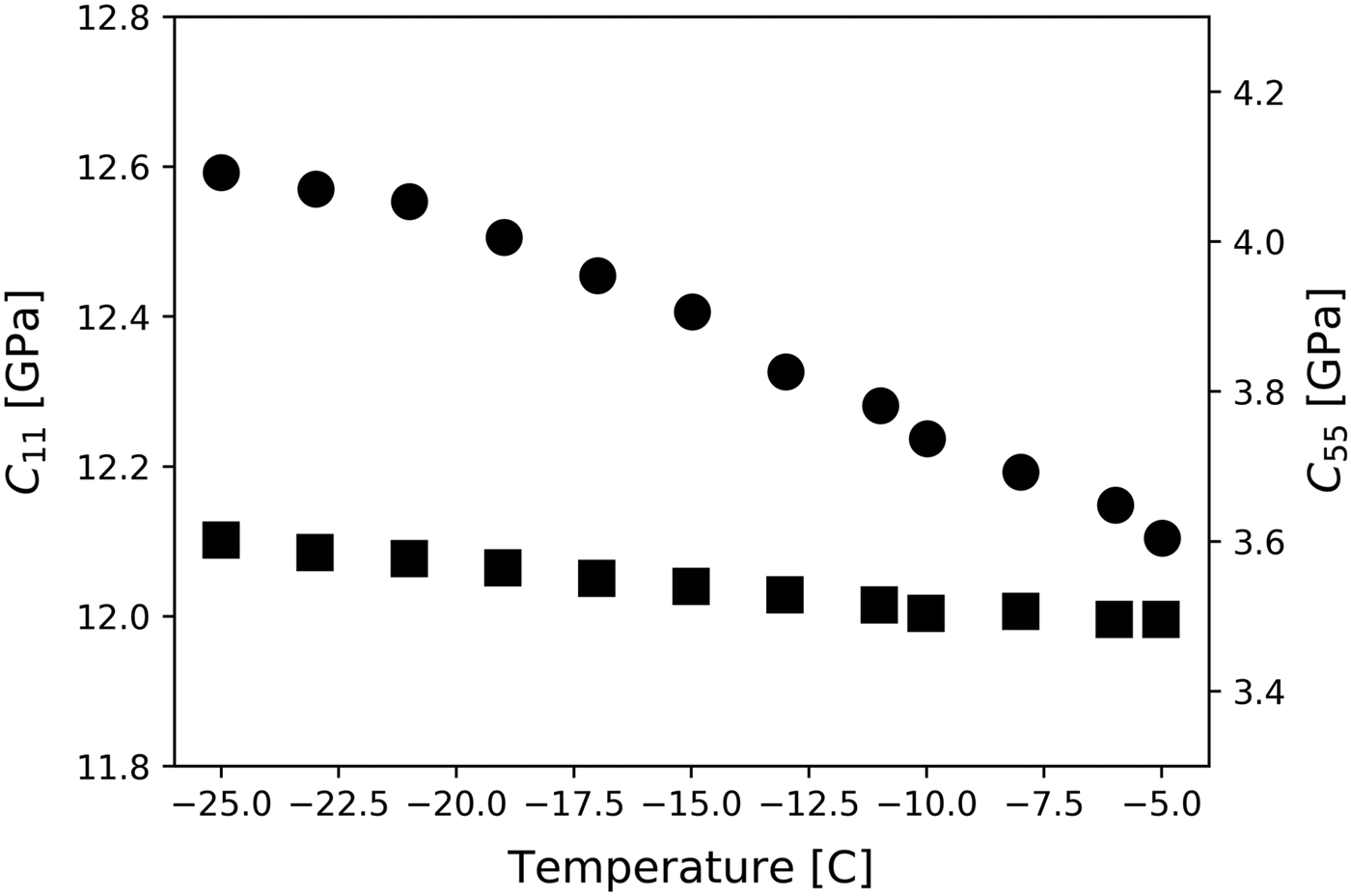
Fig. 1. Elastic stiffness coefficients C ₁₁ (circles and left scale) and C ₅₅ (squares and right scale) as a function of temperature estimated by Vaughan and others (2016) based on resonant ultrasound spectroscopy measurements.

To estimate the mechanical properties of the grain boundaries based on the measured elastic stiffnesses, we use a model in which the grain boundaries are represented as imperfectly bonded interfaces, across which traction is continuous, but displacement may be discontinuous (Schoenberg, 1980; Kachanov, 1992). The elastic anisotropy caused by the presence of the grain boundaries is represented in terms of a second-rank and a fourth-rank tensor (Sayers and Kachanov, 1995) that quantify the dependence of the elastic stiffness coefficients on the normal and shear compliances of the grain boundaries and their orientation distribution. The model allows components of these tensors to be estimated from measurements of the elastic stiffness coefficients of polycrystalline ice as a function of temperature. The next section describes the model used. Following this, results from applying the model to estimate the mechanical properties of the grain boundaries from the elastic stiffness estimates of Vaughan and others (2016) are presented, followed by the conclusions of this work.

MODEL DESCRIPTION

We represent the effects of the grain boundaries on the elastic stiffnesses in the presence of melt, by modeling the grain boundaries as locally flat imperfectly bonded interfaces, across which traction t is continuous as shown schematically in Figure 2. The displacement u may be different on opposing sides of the grain boundary due to the deformation of the boundary (Schoenberg, 1980). It is convenient to introduce a Cartesian reference set of axes x ₁, x ₂, x ₃, fixed in the sample. The difference in displacement of opposing sides of the grain boundary is denoted by [u], with Cartesian components [u _i], i = 1,  2,  3. For small deformations, as occurs in the resonant ultrasound spectroscopy measurements of Vaughan and others (2016), [u] is linear in the traction, and the i-th component may be written as

(1)$$[u_i] = B_{ij}t_j.$$

In this equation, as elsewhere in this paper, the Einstein summation convention, in which a summation is made over repeated indices (i,  j,  k,  l = 1,  2,  3), is used. The quantity t _j is the j-th component of the traction vector, and B _ij are components of the second-rank grain boundary compliance tensor B. Equation (1) describes the mechanical behavior of a grain boundary modeled as an imperfectly bonded interface between grains, and depends on the nature of the contacts between grains, the number of contacts per unit area, the deformability of any open regions between grain contacts, any fluids within the grain boundary, etc. If there is rotational symmetry around the normal to the grain boundary, it follows from Schoenberg (1980) and Kachanov (1992) that B _ij may be represented in terms of a normal compliance B _N and shear compliance B _S as follows:

(2)$$B_{ij} = B_{\rm N}n_in_j + B_{\rm S}(\delta _{ij} - n_in_j),$$

where n _i is the i-th component of the unit normal n to the grain boundary. The Kronecker delta δ _ij has the property that δ _ij = 1 if i = j, and δ _ij = 0 if i ≠ j. The normal and shear grain boundary compliances B _N and B _S will be used below to determine the contribution of grain boundaries to the elastic stiffness coefficients of polycrystalline ice.

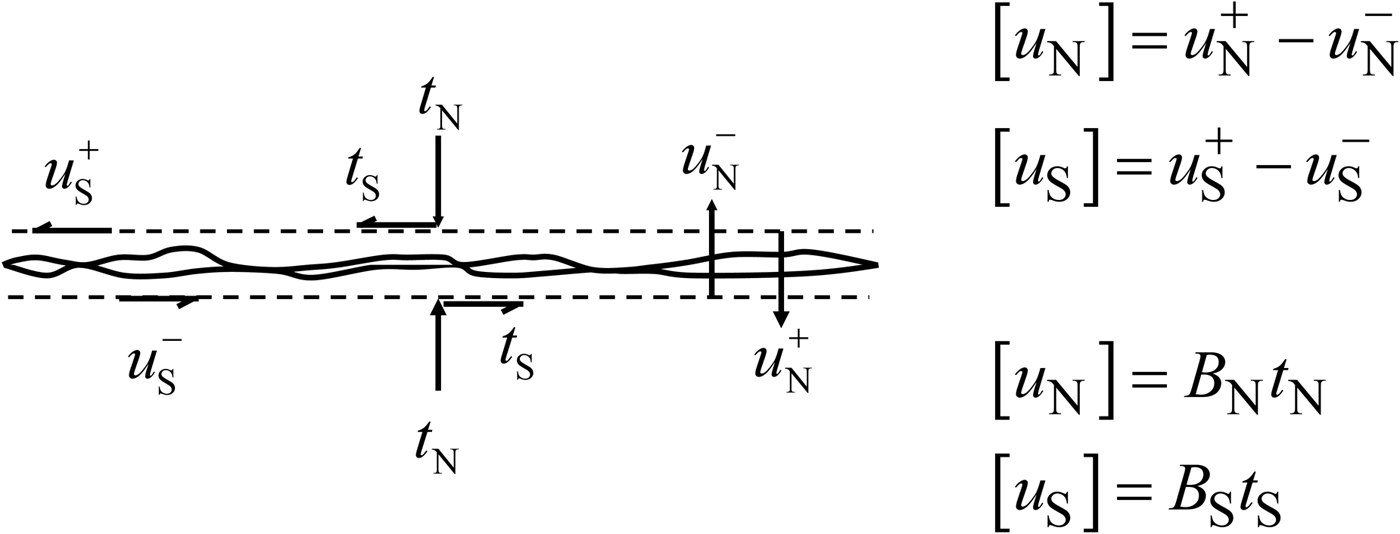
Fig. 2. Schematic representation of part of a grain boundary in ice modeled as a locally flat imperfectly bonded interface. The normal and shear displacements of the upper face of the grain boundary are denoted by $u_{\rm N}^ + $ and $u_{\rm S}^ + $, whereas those of the lower face are denoted by $u_{\rm N}^ - $ and $u_{\rm S}^ - $. The normal and shear components of the difference in displacement between opposing sides of the grain boundary are given by $[u_{\rm N}] = u_{\rm N}^ + - u_{\rm N}^ - $ and $[u_{\rm S}] = u_{\rm S}^ + - u_{\rm S}^ - $, and are related to the normal and shear tractions t _N and t _S by the equations shown in the figure.

We denote the components of the fourth-rank elastic stiffness tensor C of polycrystalline ice by C _ijkl (i, j, k, l = 1, 2, 3), and the components of the fourth-rank elastic compliance tensor S of polycrystalline ice by S _ijkl.

In the presence of grain boundaries having different orientation, the S _ijkl may be written in the form:

(3)$$S_{ijkl} = S_{ijkl}^0 + \Delta S_{ijkl},$$

where $S_{ijkl}^0 $ are the components of the elastic compliance tensor S⁽⁰⁾ for the case in which the effect of grain boundary compliance may be considered negligible, as will be assumed to be the case at the lowest temperature (−26°C) in the experiments of Vaughan and others (2016). For an anisotropic orientation distribution of ice crystals, S⁽⁰⁾ is anisotropic, although estimates of elastic anisotropy in their samples by Vaughan and others (2016) indicated a P-wave anisotropy of order 0.1%, so that the samples may be treated as elastically isotropic. S⁽⁰⁾ includes also the effect of any porosity in the interior of the ice crystals, which is assumed not to vary with temperature. This porosity is estimated by Vaughan and others (2016) to be of order 1%. The components ΔS _ijkl of the excess compliance tensor due to the presence of the grain boundaries can be written in terms of a second-rank tensor α and fourth-rank tensor β (Sayers and Kachanov, 1995) as:

(4)$$\Delta S_{ijkl} = \displaystyle{1 \over 4}(\delta _{ik}\alpha _{\,jl} + \delta _{il}\alpha _{\,jk} + \delta _{\,jk}\alpha _{il} + \delta _{\,jl}\alpha _{ik}) + \beta _{ijkl}.$$

The components α _ij and β _ijkl of α and β are defined by

(5)$$\alpha _{ij} = \displaystyle{1 \over V}\sum\limits_{r = 1}^N {B_{\rm S}^{(r)} n_i^{(r)} n_j^{(r)} A^{(r)}}, $$

(6)$$\beta _{ijkl} = \displaystyle{1 \over V}\sum\limits_{r = 1}^N {\left( {B_{\rm N}^{(r)} - B_{\rm S}^{(r)}} \right)n_i^{(r)} n_j^{(r)} n_k^{(r)} n_l^{(r)} A^{(r)}}. $$

The sum is over the N grain boundaries in volume V. The quantities $B_{\rm N}^{(r)} $ and $B_{\rm S}^{(r)} $ are the normal and shear compliance of the r-th grain boundary in volume V, $n_i^{(r)} $ is the i-th component of the local unit normal to the r-th grain boundary, and A ^(r) is the local area of the grain boundary (Sayers and Kachanov, 1995). Because the components of the unit normal to the grain boundaries appear as products in (5) and (6), it follows that α _ij and β _ijkl are symmetric with respect to all rearrangements of the indices so that β ₁₁₂₂ = β ₁₂₁₂,  β ₁₁₃₃ = β ₁₃₁₃ , etc.

This model allows information on grain boundary compliance to be obtained from measured elastic stiffnesses, as will be illustrated next using the elastic stiffnesses of polycrystalline ice measured by Vaughan and others (2016) as a function of temperature. The samples used by Vaughan and others (2016) were found to be close to isotropic. Assuming an isotropic orientation distribution of grain boundaries, several components α _ij and β _ijkl are zero, and the non-vanishing components can be written in terms of quantities α and β, defined as follows (Sayers and Kachanov, 1995):

(7)$$\alpha _{11} = \alpha _{22} = \alpha _{33} = \alpha, $$

(8)$$\beta _{1111} = \beta _{2222} = \beta _{3333} = \beta $$

and

(9)$$\beta _{1122} = \beta _{1133} = \beta _{2233} = \beta _{1212} = \beta _{1313} = \beta _{2323} = \beta /3.$$

The non-vanishing components ΔS _ijkl follow from (4) as (Sayers, 2002):

(10)$$\Delta S_{1111} = \Delta S_{2222} = \Delta S_{3333} = \alpha + \beta, $$

(11)$$\Delta S_{1122} = \Delta S_{1133} = \Delta S_{2233} = \beta /3,$$

(12)$$\Delta S_{1212} = \Delta S_{1313} = \Delta S_{2323} = \alpha /2 + \beta /3.$$

The elastic stiffness tensor C is obtained as the inverse of the compliance tensor S with components S _ijkl given by (3) with the ΔS _ijkl given by (10)–(12).

The symmetry of the elastic stiffness tensor C and the elastic compliance tensor S enables use of a condensed 6 × 6 two-index notation (Voigt, 1910; Nye, 1985) in which pairs of subscripts ij and kl are abbreviated by single subscripts according to the convention, 11 → 1, 22 → 2, 33 → 3, 23, 32 → 4, 13, 31 → 5 and 12, 21 → 6. For an isotropic medium, the elastic stiffness components C _ij in two-index notation may be written in terms of the isotropic bulk modulus K and shear modulus μ as

(13)$$\left[ {C_{ij}} \right] = \left[ {\matrix{ {K + 4\mu /3} & {K - 2\mu /3} & {K - 2\mu /3} & 0 & 0 & 0 \cr {K - 2\mu /3} & {K + 4\mu /3} & {K - 2\mu /3} & 0 & 0 & 0 \cr {K - 2\mu /3} & {K - 2\mu /3} & {K + 4\mu /3} & 0 & 0 & 0 \cr 0 & 0 & 0 & \mu & 0 & 0 \cr 0 & 0 & 0 & 0 & \mu & 0 \cr 0 & 0 & 0 & 0 & 0 & \mu \cr}} \right].$$

It then follows from (3), (4) and (10)–(12) that the bulk modulus K and shear modulus μ are given in terms of the bulk modulus K ₀ and shear modulus μ ₀ of the sample when the ice crystals are fully bonded, as will be assumed to be the case at the lowest temperature (−26°C) in the experiments of Vaughan and others (2016), by

(14)$$K = \displaystyle{{K_0} \over {1 + 3K_0(\alpha + 5\beta /3)}},$$

(15)$$\mu = \displaystyle{{\mu _0} \over {1 + 2\mu _0(\alpha + 2\beta /3)}}$$

(Sayers and Han, 2002). These equations allow α and β to be determined from measurements of the elastic stiffness coefficients C ₁₁ = K + 4μ/3 and C ₄₄ = μ, and knowledge of K ₀ and μ ₀. For an isotropic orientation distribution of grain boundaries, it follows from (5) and (6) that B _N/B _S = 1 + 5β/3α (Sayers and Han, 2002), where the average normal and shear compliance are denoted by B _N and B _S, and this estimate is valid when the shear compliance of the grain boundaries is non-zero. This allows B _N/B _S to be estimated from the ratio β/α obtained from (14) and (15).

RESULTS

Since α and β have units of compliance, it is more convenient to plot the dimensionless quantities μ ₀α and μ ₀β where μ ₀ is the shear modulus of the sample when the ice crystals are fully bonded. Figure 3 shows the values of μ ₀α and μ ₀β obtained from (14) and (15), where K and μ are calculated from C ₁₁ and C ₄₄ shown in Figure 1 using the isotropic equations K = C ₁₁ − 4C ₄₄/3, μ = C ₄₄. Note that α and β are of opposite sign, and this implies that B _N/B _S < 1, as seen from (5) and (6). The grain boundaries appear, therefore, to be more compliant in shear than under a normal stress.

Fig. 3. Values of normalized grain boundary compliance tensor components μ ₀α (circles) and μ ₀β (squares) estimated from the elastic stiffness coefficients C ₁₁ and C ₅₅ measured by Vaughan and others (2016) based on resonant ultrasound spectroscopy.

The theory used to estimate μ ₀α and μ ₀β from the measured elastic stiffnesses C ₁₁ and C ₅₅ is a general representation of the mechanical behavior of a grain boundary modeled as an imperfectly bonded interface between grains, and includes the mechanical behavior of the contacts between grains, the number of contacts per unit area, the deformability of any open regions between grain contacts, the fluid distribution within the grain boundary, etc. It is interesting, however, to compare the results for B _N/B _S obtained from the measurements of Vaughan and others (2016) with a simple model in which the grain boundaries are considered to be porous, the pores being assumed to be oblate spheroids with radius a and aspect ratio c/a in a homogeneous background medium with shear modulus μ and Poisson's ratio ν. An oblate spheroid is an ellipsoid obtained by rotating an ellipse about its minor axis, with equatorial dimension a greater than the polar dimension c. The additional compliance introduced by the spheroid depends on the properties of the host medium and the fluid within the spheroid. For the case of spheroidal voids with the ability of fluid exchange via small pathways, Hudson and others (1996) show that for a random distribution of coplanar spheroids in an infinite domain, the ratio B _N/B _S is

(16)$$\displaystyle{{B_{\rm N}} \over {B_{\rm S}}} = \displaystyle{{\left( {1 + A} \right)\left( {1 - \nu /2} \right)} \over {1 + B}},$$

where

(17)$$A = \displaystyle{{4a} \over {\pi c}}\left( {\displaystyle{{i\omega \eta _{\rm f}} \over \mu}} \right)\left( {\displaystyle{{1 - \nu} \over {2 - \nu}}} \right),$$

(18)$$B = \left[ {\displaystyle{{2a} \over {\pi c}}\displaystyle{{\kappa _{\rm f}} \over \mu} \left( {1 - \nu} \right)} \right]\left( {1 - \displaystyle{{3i\kappa _{\rm f}k^2K_r} \over {4\pi \nu a^2c\omega \eta _{\rm f}}}} \right)^{ - 1}.$$

In (17) and (18), $i = \sqrt { - 1} $, κ _f and η _f are the bulk modulus and viscosity of the fluid, respectively, ω is the angular frequency, k is the wavenumber and K _r is the permeability of the medium including the contribution of the grain boundaries. Because (16)–(18) are frequency dependent and have a real and imaginary part, this will lead to dispersion and attenuation of the elastic wave. These effects lie outside the scope of the current work, however, whose objective is to examine the dependence of the real part of the elastic stiffness coefficients on the grain boundary compliances.

For low permeability, as would occur if the aspect ratio c/a is small, or if the grain boundaries are poorly connected, the compliance ratio in (16) simplifies to

(19)$$\displaystyle{{B_{\rm N}} \over {B_{\rm S}}} = \displaystyle{{\left( {1 + A} \right)\left( {1 - \nu /2} \right)} \over {\left[ {1 + \displaystyle{{2a} \over {\pi c}}\displaystyle{{\kappa _{\rm f}} \over \mu} \left( {1 - \nu} \right)} \right]}}.$$

A decrease in the aspect ratio c/a and an increase in the bulk modulus of the fluid κ _f both lead to a decrease in compliance ratio.

Figure 4 shows the variation in B _N/B _S as a function of temperature determined from the results shown in Figure 3. It is seen that B _N/B_S < 1 implying that the grain boundaries are more compliant in shear than in compression. The ratio B _N/B _S is seen to be small at low temperatures, but increases as temperature increases, implying that the normal compliance increases relative to the shear compliance with increasing temperature.

Fig. 4. Variation in the ratio B _N/B _S of the normal compliance B _N to shear compliance B _S as a function of temperature determined from the results shown in Figure 3.

CONCLUSION

This paper presents a determination of the normal and shear compliance of grain boundaries in polycrystalline ice from the temperature-dependent elastic stiffness measured by Vaughan and others (2016). The approach is formulated in terms of a second-rank tensor α and fourth-rank tensor β that depend on the orientation distribution as well as the normal and shear compliance of the grain boundaries. This allows one to obtain the normal and shear compliance of the grain boundaries as a function of temperature from measurements of the elastic stiffness coefficients. We applied the method to estimates of elastic stiffness coefficients based on resonant ultrasound spectroscopy measurements on polycrystalline ice between −26°C and −5°C. Notably, α and β were found to have opposite signs. This implies that the ratio of the normal to shear compliance B _N/B _S < 1. Grain boundaries in polycrystalline ice are, therefore, more compliant in shear than in compression. The ratio B _N/B _S is small at low temperatures, but increases as temperature increases implying that the normal compliance increases relative to the shear compliance as temperature increases.

It should be noted that the results presented are obtained for a single sample investigated by Vaughan and others (2016) that has a particular grain size distribution. It would be interesting to repeat these calculations for other samples having a different size distribution of ice crystals, once such measurements become available, since this will allow the grain size dependence of the grain boundary compliance to be investigated. Also, since the number of grain boundaries will increase with decreasing grain size, measurements of ultrasonic attenuation on samples having different grain size distributions may allow the effects of scattering to be separated from attenuation due to viscous damping resulting from the effects of the viscosity of the fluid at the grain boundaries. This appears to be a promising area for future work.