Introduction
Of the methods available for the measurement of the depth of naturally occurring ice masses, radio-echo sounding is the one most frequently used. The technique, which has now been developed to a fairly advanced stage for remote sensing, requires a knowledge of the velocity or, equivalently, the permittivity in ice at radio-frequencies. The value of the relative permittivity ∊’ which has generally been used for the calculation of the depth of ice by this technique is either an approximate value of the limiting high-frequency permittivity ∊«, which in practice is obtainable only from an accurate extrapolation of the permittivity, dielectric loss and frequency data by a suitable method (Reference ColeCole, 1955),, or the value of ∊’ measured at microwave frequencies. Reference Robin.de, Robin.de, Evans and BaileyRobin and others (1969) reviewed the interpretation of radio-echo sounding and, after examining the available data for ∊’, proposed that ∊’ = 3.17 Ʊ0.07, independent of temperature in the frequency range 10 to 105 MHz, would be a useful approximation in these calculations.
Several sets of measurements (Reference Von HippelVon Hippel, 1954; Reference YoshinoYoshino, 1961; Reference GoughGough, 1972; Reference Robin de Robin 1975), have been reported in the MHz frequency range, but a considerable variation in the ∊’ values is found between the various sets. The ∊’ values near 35 MHz, which are particularly useful in the interpretation of radio-echo sounding, are reported only by Yoshino who found the values to be much higher than 3.17. The purpose of this study was to measure accurately the dielectric properties of ice under a variety of conditions at 35 and 60 MHz to help provide the data for possible use in glaciology. This paper reports some results of ∊’ and attenuation for ice Ih as a function of temperature, pressure, crystal orientation, and plastic deformation.
Experimental methods
The measurements of capacitance and equivalent parallel resistance were carried out by means of a RX-Meter Type 2 50-A (manufactured by Boonton Radio Corp., Boon ton, New Jersey). The instrument is completely self-contained and consists of a refined Schering bridge, together with an associated oscillator which generates frequencies in the range 0.5-250 MHz, an amplifier, a null detector and a power supply. The frequency of the oscillator was accurately adjusted using an electronic counter. In its normal operation the RX-Meter can be used to measure a capacitance up to 20 pF by means of a dial graduated in 0.1 pF steps. The capacitance can be readily estimated to within 0.025 pF with the help of a magnifying glass.
A two-terminal coaxial cylindrical capacitor shown in Figure 1 was used as a dielectric cell. It consists of a stainless steel outer cylinder c which had an outside diameter of 22.2 mm, an inside diameter of 12.65 mm, and was 69.1 mm long. This cylinder was threaded to receive the gland nut A at one end and the brass adapter E at the other, B is a mushroom-shaped piston which has a 1.5 mm hole extending to within 3 mm of the bottom of B for the purpose of accepting a thermocouple. The clearance between B and C was kept at about 0.03 mm to prevent the extrusion of ice. C acts as the low electrode maintained at ground potential. The electrode D, which is at high potential, is an interchangeable stainless steel cylinder with an outside diameter of either 9,53 mm or 6.53 mm and a length of 36.65 mm, 7.87 mm of which was cut to an outside diameter of 4.22 mm and threaded to accept the brass adapter-pin H. D is seated on the concentric step cut out of the adapter E, but insulated from E by means of two 1 mm thick “Teflon” (polytetrafluoroethylene) discs F placed on either side of a 1.14 mm thick disc G made from 0.80% carbon steel hardened to 52 Rockwell C. The dimensions of H and E, and their respective positions, are such that together they form a coaxial N-type connector. Thus the complete cell assembly can be screwed on to the plug provided on top of the RX-Meter. The “Teflon” insulator F acts as a pressure seal for the ice and for liquids. The dielectric cell has a nominal geometric capacitance of 6 pF with the 9,53 mm diameter electrode and 4 pF with the 6.53 mm diameter electrode with a stray capacitance in both cell assemblies of 0.3 pF. The capacitance of the empty cell was measured throughout the temperature range +20° C to —60° C and was found to be constant within the detection limit of the instrument. The ∊’ measured with the two assemblies agreed to within ±0.3%.
In order to minimize the effects due to stray capacitance and inductance, the dielectric cell was mounted directly on top of the instrument, thus avoiding the use of connecting cables.
The ∊’ of ice was obtained by the method of substitution as follows. Eight mixtures of varying concentrations of chlorobenzene in benzene were prepared. The dielectric permittivity of each mixture, which was within the range 3.08-3.25, was measured to within ±0.05% at —5° C and +20° C and at 1 kHz, using a parallel-plate dielectric cell and a General Radio 1615 capacitance bridge. The coaxial dielectric cell was filled with each of the chlorobenzenc-benzene mixtures and the capacitance of the cell at — 5° C and +20° C was read on the RX-Meter dial at the desired frequency. Thus a set of calibration curves of thepermittivity of the cell content against the RX-Meter dial reading was obtained at 35 and 60 MHz. The dielectric cell was then filled with ice and the RX-Meter reading for the cell containing ice was converted to ∊’ using the calibration curves. After the measurements on a sample of ice over a range of temperature and frequency were completed, the calibration of the dielectric cell was checked and corrections, if any, were applied to the ∊’ values.
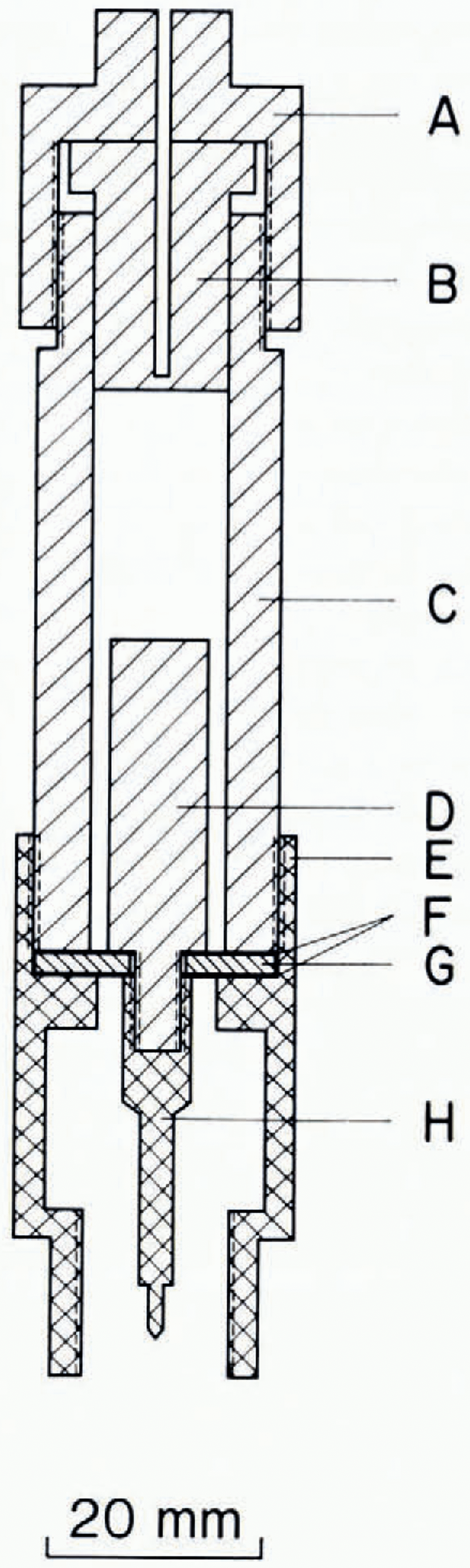
Fig. 1. The coaxial cell for measurement of dielectric properties at radio-frequencies.
The conductance dial on the RX-Meter is graduated on a logarithmic scale and therefore has poor resolution in part of the conductance range. The first 13 samples of polycrystalline ice were measured with the unmodified meter. This gave estimates of conductance with a very large uncertainty but did not influence the ∊’ measurements. For an accurate determination of the resistance (and conductance) of 6 samples of polycrystalline and 5 samples of single-crystal ice in the latter part of the study, a circular vernier dial divided into 250 divisions per turn was mounted on the shaft of the resistance dial of the meter. The vernier dial readings were calibrated using a set of non-inductive resistors of accurately known resistance in the range 104-106 Ω. This calibration was used to obtain the equivalent parallel resistance of ice for which the data are given. Measurements with the cell on liquids and solids of known d.c. conductance showed no surface effect on the conductivity at the frequencies investigated. The correction for the stray capacitance of the high-frequency cell was applied in the calculation of the imaginary part of e and the loss tangent tan δ. The values of ∊’ of ice are accurate to within ±0.3% and those of tan δ to within ±2%. These values are free from systematic errors.
The temperature was measured by means of a calibrated copper-constantan thermocouple which was kept inside the well drilled into the piston of the dielectric cell. The ice contained in the dielectric cell was cooled in a cold chamber and, after the desired temperature had been attained, the cell was insulated by means of 5 cm thick polystyrene foam. After the temperature had reached equilibrium, the insulated cell was taken out, mounted on the RX-Meter and the readings of capacitance and resistance taken. Because of heat conduction from the RX-Meter terminal to the dielectric cell, the temperature of the ice increased by 0.5±0.2° C during the measuring time. A correction for the temperature change was applied. For measurements above —4° C, the dielectric cell was surrounded by a glass jacket through which cold methanol from a thermostatically-controlled bath was circulated. The temperatures reported here are accurate within ±0.2° C.
To investigate if any change in the bridge characteristics, and therefore in the calibration, occurred as a result of cooling the RX-Meter terminals, the bridge terminals were cooled to — 30 ° C. No change in the bridge reading was detected.
A serious problem in the study of the electrical properties of ice is caused by the presence of voids of indeterminate dimensions which result from cracks in the sample, from the much lower solubility of air in ice than in water, or from the shrinking of ice away from the electrode as the temperature is lowered. In order to avoid the formation of such voids, the polycrystalline ice was prepared in the following manner. Double distilled de-ionized water was evacuated in a glass container for 2 h or more to remove the dissolved air. The water was then poured into the coaxial cell (capacity 7 ml) and was allowed to freeze in a cold chamber at — 5 ° C The freezing process proceeded from the circumference of the water inwards. When the water was completely frozen the slightly warm piston B was inserted, thus melting a thin layer of surface ice which was then allowed to refreeze. The gland nut was tightened enough to generate a pressure of 50°20 bar on the ice which acted as its own pressure-transmitting medium. This pressure was calculated from the number of turns through which the gland nut was tightened. Twice during this study, the water supercooled to c. —5° C before freezing. The ∊’ of the ice thus obtained, measured within 1 h of freezing, was identical to the value measured after four days.
After completion of a temperature and frequency run, the cylinder C was slightly warmed and unscrewed from E, thus exposing the ice with the electrode D embedded in it. With a magnification of x 2, no air bubbles were seen in the ice. An examination of four samples under crossed polarizing filters showed a crystal size of c. 1 mm. While the orientation of the crystals may not be entirely random, we did not observe any obvious c-axis orientation.
The single crystal of ice was prepared from de-ionized water contained in a polyethylene tube using a zone-refining method. Cylindrical pieces of ice cut from a large single crystal were oriented with the cylinder axis parallel to the c-axis to within ±2° using crossed polarizing filters, and then machined into the shape of a hollow cylinder of outside diameter 12.6 mm, inside diameter 6.5 mm and length 63.5 mm. The sample was fitted snugly into the dielectric cell while still held in the lathe and the excess portion of the crystal was cut off. The cell containing the ice was then transferred to an airtight glass container kept in a cold chamber at — 3° C. The air space of diameter 6.5 mm, which remained on top of the high-potential electrode after the machined piece of ice had been fitted into the dielectric cell, was filled with de-ionized double distilled water which was at 0±0.5° C and the container was evacuated for about 30 min. This procedure ensured that any possible air gaps between the electrode and ice had been evacuated and were now filled with ice. The dielectric cell was taken out of the container, the piston B inserted and the gland nut tightened.
Results and discussion
3.1.The permittivity
The relative permittivity ∊’ of polycrystalline and single-crystal ice oriented with the electric field perpendicular to the c-axis is plotted against temperature in Figure 2. Measure-ments on 19 samples of polycrystalline ice and 5 samples of single-crystal ice, which are given in Figure 2, clearly indicate the scatter of the results. Interpolated values of ∊’ at integral temperatures are given in Table I. The ∊’ at —° C decreases from 3.208 to 3.200, and at —20° C from 3.178 to 3.167, as the frequency is raised from 35 to 60 MHz. The amount of decrease is greater than the experimental error and indicates a small amount of dielectric dispersion at these frequencies.
The ∊’ values may be compared with those given in the literature. Reference EvansEvans (1965) and Reference Robin.de, Robin.de, Evans and BaileyRobin and others (1969) have already reviewed ∊’ values at different frequencies and therefore we should be concerned only with those results which have been obtained at frequencies comparable with ours.

Fig. 2. The relative permittivity of ice at 35 and 60 MHz plotted against temperature. О, polycrystalline; ▴ single crystal perpendicular to the c-axis.
Table 1. Relative permittivity and dielectric loss tangent of ice ih as a function of temperature

Reference YoshinoYoshino (1961) has made dielectric measurements on natural ice of density 0.91 Mg m −1in Antarctica from — 18° C to —36° C over the MHz frequency range. His value for ∊’ o approximately 3.6 interpolated at 35 MHz is much higher than our value of 3.18 at — 18° C. Westphal (as quoted by Reference EvansEvans 1965), has measured the permittivity of annealed ice obtained from the Greenland ice sheet. For ice of density 0.900 Mgm−3, his value of 3.20 at —5° C and 150 MHz agrees with ours of 3.186 at 60 MHz. In view of the approximately 2% difference between the respective densities of the Greenland ice and the laboratory-grown ice, the agreement of our data with that of Westphal is surprising. The significance of this agreement is difficult to ascertain as the details of Wcstpha’s method remain unpublished. Within their uncertainty of ±2% Gough’s values of ∊«, obtained from extrapolation are in agreement with our values of x03B5;’.
The permittivity of ice has also been evaluated from field measurements of the velocity of electromagnetic waves. Since the accuracy of these measurements is similar to that of the capacitance measurements, it is worthwhile to compare the results obtained by the two methods.
The velocity of a radio-frequency wave in natural ice containing air bubbles in situ obtained from radio-echo sounding, or more recently from an interferometric technique, can be appropriately extrapolated to a value of x03B5;’ corresponding to that of pure (bubble-free) ice using the density measurements. Reference Pearce and WalkerPearce and Walker (1967) have derived ∊’ = 3.3x03B1;0.04 for deep ice (temperature not known) of density 0.920 Mg m−3 from the propagation time of a 30 MHz radar pulse in the ice cap at Camp Century, Greenland. From wide-angle, echo-time measurements interpreted in the light of their field observations in an ablation zone on Skelton Glacier, Antarctica, Reference Jiracek, Bentley and CraryJiracek and Bentley (1971) have concluded that the best estimate of ∊’ for pure ice at 35 MHz is 3.21. Reference Robin de Robin (1975) measured the velocity of a 440 MHz wave using an interferometric technique in the bore holes on the ice cap on Devon Island, Canada, and obtained a value of 167±0.3 m μs−1 for ice of density 0.917 Mg m−3at -20° C. The ∊’ calculated from his data is 3.200°0.011.
Considering the errors in the density data of bubble-contaminated ice and in the extrapolation involved in obtaining the velocity for pure ice, the value of ∊’ of natural ice in situ from the major areas (Greenland, Antarctica, and the Arctic) agrees satisfactorily with that of the laboratory-grown ice. We believe that this agreement illustrates a significant fact, namely, that at frequencies relevant to radio-echo sounding little difference exists between the dielectric permittivity of laboratory-grown ice and natural ice in situ.
3.2.The attenuation
Absorption of an electromagnetic wave in ice is measured as the attenuation a in a radio-echo sounding experiment. The dielectric loss tangent tan δ measurements are, therefore, usefully reported as the rate of attenuation with respect to thickness of ice. The α at the different temperatures is given by:
For tan δ ≪ 0.1 the equation reduces to,
Or
where α is the attenuation in appropriate units, ω is the angular frequency, c is the speed of light and tan x03B4; = ∊(ш)/∊’(ш). The ∊’(ш) and ∊(ш) are the real and imaginary parts of the relative dielectric permittivity, respectively, at a frequency ω. Interpolated values of tan κ at integral temperatures are given in Table I.
The attenuation in dB/100 m calculated from Equation () is plotted against temperature in Figure 3. The attenuation calculated by Reference Robin.de, Robin.de, Evans and BaileyRobin and others (1969) using Westphal’s values of tan δ for Greenland ice at 150 MHz is considerably lower than ours at temperatures greater than —15° C. The significance of this discrepancy cannot be unambiguously determined, for, in addition to the difference in the frequency of our respective measurements, the ice sample used by Westphal was considerably less dense than the one used in our study.
The temperature of the main bulk of a natural ice mass has been evaluated (Reference Robin.de, Robin.de, Evans and BaileyRobin and others, 1969) from field measurements of the rate of increase of a with (he depth of ice at 35 MHz, and, by using Westphal’s laboratory measurements of attenuation at 150 MHz, as a function of temperature for the ice obtained from the TUTO tunnel, Greenland. The temperature of ice for surface elevations below 922 m in the ice sheet of north-western Greenland near TUTO has thus been estimated to be — 1 ° C. Our values of attenuation at 35 MHz, if valid for Greenland ice, will place this temperature at —2.5° C.
3.3. The anisotrapy of ∊’ and δ and radio-echo sounding
As is evident in Figures 2 and 3, the ∊’ and δ values of polycrystalline ice agree with those of single-crystal ice (oriented perpendicularly to the c-axis) to within ±0.3%. This agreement, however, does not indicate that the polarization in ice is absolutely isotropic for, within the experimental error of ±0.3%, a maximum difference of about 1 % between the ∊ ’ and the δ, measured parallel and perpendicular to the c-axis, can remain undetected in our measurements; as a calculation from the following equation would show,
where χ represents the ∊δ, etc.
The anisotropy of polarization in ice is of considerable significance in the interpretation of echo strengths in radio-echo sounding. Therefore its discussion is desirable. It has been held that Reference Von Hippel, Von Hippel, Westphal, Knoll, M a idique, Mykolajewycz and glesiasVon Hippel and others’ (1969, 1971) measurements indicate ice to be anisotropic at radio-frequencies. Reference Evans and GudmandsenEvans (1970) suggested that this anisotropy might account for the observation of possible layers at depths greater than 2 km in Central Greenland. The suggestion does not appear meaningful as an analysis of the data of Reference Von Hippel, Von Hippel, Knoll and WestphalVon Hippel and others (1969, 1971), given as follows, indicates no anisotropy of polarization at 35 MHz. The ∊’ and δ at 35 MHz can be calculated from the equations,

and

where Д∊п is the contribution from, and rn the relaxation time of, the polarizations due to molecular orientation, space charge, Maxwell-Wagner effect, etc., each represented by a simple Debye relaxation process, ση is the d.c. conductivity and ∊o is the permittivity of free space (8.854 X 10−12-F m-1).
From Equations (2) and (3), using Von Hippel and others’ values for the N, Δc, τ and σ0 of ice measured perpendicular to the c-axis at —3.9°C, we calculate ∊’ = 3.13 and œ = 2.64 dB/100 m. For the same sample of ice at — 10.0°C, ∊’ = 3.15 and δ= 1.43 dB/100 m. Using their data for 4 samples of ice measured parallel to the c-axis at —4.0±0.1° C, our calculation gives a value of ∊’ which ranges from 3.00 to 3.21 and of a from 2.92 to 10.10dB/100 m. For the same samples of ice at — 10.05±0.05° C our calculated value of ∊’ (from the data of Von Hippel and others) ranges from 3.06 to 3.21 and of a from 1.65 to 1.69 dB/ 100 m. The difference between the respective values of ∊’ and δ of the 4 samples of ice measured parallel to the c-axis, and the reported negative temperature coefficient of the ∊ж (Reference Von Hippel, Von Hippel, Westphal, Knoll, M a idique, Mykolajewycz and glesiasVon Hippel and others, 1969, 1971) no doubt reflect the uncertainty of their measurements and/or analysis. Within this uncertainty, the

Fig. 3. The attenuation in ice at 35 and 60 MHz plotted against temperature, O, pokcrystalline; ▴, single crystal perpendicular to the c-axis.
In terms of molecular processes, the ∊’ represents the sum of contributions to the permittivity from electronic, vibrational, and orientational polarizations. It follows that a possible anisotropy of any of these processes should be reflected in the ∊’. Unfortunately, no theoretical or experimental information on the degree of anisotropy of inter- and intramolecular vibrational and orientational polarization of water molecules in ice is available. An anisotropy of electronic polarization corresponding to an
This leads us to a further point of interest. Reference HarrisonHarrison (1973), from a calculation of the effective power reflection coefficient, has concluded that a fractional change as small as 10−4in the permittivity is sufficient to produce detectable reflections in radio-echo sounding. The echo strengths observed in the Antarctic and Greenland ice sheets may, he proposed, be explained by multiple layering, if the ice crystals differed in their average orientations in these layers. If Harrison’s calculations are adequate, the difference between the optical refractive index measured parallel and perpendicular to the c-axis, corresponding to an anisotropy of permittivity due to electronic polarization in ice of 0.0037 alone could account for the observed echo strength if a sufficient change in the crystal orientation occurs in these layers.
There may be an added contribution to the anisotropy of polarization if a material which is normally isotropic is in a strained condition. This condition may be significant when dealing with glacial stresses. Since the deformation of a crystal alters the intermolccular potential, a contribution from the anisotropy of vibrational polarization could be important.
3.4.The effect of plastic deformation on ∊’ and ∊
It is often mentioned— though rarely substantiated—that the strain resulting from a plastic deformation alters the dielectric properties of ice. The somewhat high ∊’ of ice (approximately 3.5) obtained by Von Hippel at radio-frequencies has been attributed to the residual stresses in the sample (Reference EvansEvans 1965),, and it has been held (Reference Robin.de, Robin.de, Evans and BaileyRobin and others, 1969) that the elimination of strain in ice is necessary to obtain absolute ∊’ for use in radio-echo sounding. It is not, however, immediately clear to us why the ∊’ of strain-free ice should be used in the interpretation of radio-echo sounding data when ice in the large bodies of natural masses is undoubtedly in a mechanically strained state as a result of compressive and shear stresses. It is important to investigate the effect of a mechanical strain on the ∊’ and a at radio-frequencies for, the properties of a strained ice, if different from those of a strain-free ice, should precisely represent the properties of natural ice in situ.
One finds another reason for making such an investigation if one realizes that consistent and acceptable measurements of the limiting low- and high-frequency permittivity of ice have been obtained on samples which were subject to a uniaxial or a hydrostatic stress. These results are due to Reference Wörz and ColeWörz and Cole (1969), who maintained a uniaxial compressive stress on ice by spacing the parallel-plate electrodes by means of “Teflon” which has a higher isobaric expansivity than ice; to Reference GoughGough (1972), who maintained a radial stress on ice in a manner similar to that of Cole and co-workers; to Reference Auty and ColeAuty and Cole(1952) and Reference MaenoMaeno (1973), who maintained a uniaxial compressive stress on ice by spring loading the electrodes; to Reference Gough and DavidsonGough and Davidson (1970) , Reference Johari, Whalley, Whallcy , Whalley, Jones and GoldJohari and Whalley (1973) and as yet unpublished work by G. P. Johari and S. J. Jones, who applied a small hydrostatic pressure to ice. For these reasons we considered it worthwhile to investigate qualitatively the effect of plastic deformation on the ∊’ and δ of polycrystalline and single-crystal ice.
In this investigation the compressive stress on ice contained in the dielectric cell was suddenly released by removing the gland nut and the piston from the cylinder when the RX-Meter bridge was at a balance. The removal of the piston should have caused the ice to flow towards the open end of the cell in order that a uniform hydrostatic pressure of 1 bar be attained. The resulting strain pattern in the ice is complex and unknown. Within the detection limit of 0.2% no change was found in the bridge reading for a period of up to 6 h. The ice was then annealed for 38 h and the measurements were repeated. No changes in the capacitance or resistance were observed. In another experiment a uniaxial stress of 100±10 bar was applied to ice. The ice must deform plastically so that the uniaxial stress is converted into a hydrostatic stress; again, no change in the bridge reading during the period ranging from 30 s to 42 h after the application of stress was observed. Five samples of polycrystalline and three samples of single-crystal ice at approximately —4° C, —10° C and —15° C were investigated in this manner and none showed a change in the ∊’ and δ. It can be concluded, therefore, that the ∊’ and a of ice at 35 and 60 MHz is not altered when a uniaxial or a hydrostatic stress of up to 100 bar is applied.
Some information on the effect of plastic deformation on the ∊’ and δ at radio-frequencies can be obtained from a consideration of results in the literature. Reference Brill and CampBrill and Camp (1957) reported that the plastic deformation influenced the dielectric properties of polycrystalline ice at 1 kHz but offered no quantitative results. Reference Noll, Whalley, Whalley, Jones and GoldNoll (1973) found that plastic deformation of a single crystal of ice did not influence the dielectric properties in the Debye dispersion range. Reference Mae and HigashiMac and Higashi (1973) , who have recently measured the effect of a mechanical strain on the dielectric properties of single-crystal ice obtained from the Mendenhall Glacier, Alaska, concluded that the orientation polarization in ice is unaffected by a shear strain of 17.5% on the basal plane, but the polarization attributable to “space charge” effects is greatly increased. The change in the ∊’ and a on deformation was calculated from Mae and Higashi’s data using Equations (2) and (3), respectively. For a 17.5% strained ice at —21.5° C the changes in the ∊’ and δ. at 35 MHz measured perpendicular to the c-axis are 4.7 X 10−13 and 4.8 x 10−3 dB/100 m, respectively. The changes in the ∊’ and δ measured parallel to the c-axis at —16.6° C are similarly small. The analysis of their results seems to support our qualitative observation that the effect of a mechanical strain on the ∊’ and a of ice is so small as to be undetectablc.
4. Conclusion
The permittivity of ice at 35 MHz in the temperature range —25° C to —0.2 ° C is within ±1% of the value of 3.17±0.07 preferred by Reference Robin.de, Robin.de, Evans and BaileyRobin and others (1969). The agreement should be gratifying. Since the error in the echo-time measurements in radio-echo sounding is generally about 1%, little improvement on the calculation of the depth of ice would be made by using our value over the one preferred by Robin and others.
Natural ice masses contain a significant amount of air bubbles, dust and other organic and inorganic materials as impurities. For this reason our data, which were obtained with pure ice, may be of little direct use in the interpretation of the attenuation results obtained during radio-echo sounding, although they are more precise than any other presently available.
It may be mentioned that the properties of Antarctic, ice are observed to be somewhat different (Reference Fitzgerald and ParenFitzgerald and Paren, 1975) from that of laboratory-grown ice in the frequency range 50 Hz to 10 kHz. It will be interesting to see if the difference observed at low frequencies persists at 35 and 60 MHz. We hope that our work will stimulate interest in laboratory measurements on natural ice at those frequencies which are relevant to radio-echo sounding.
Experiments have shown that the anisotropy of polarization in ice at radio-frequencies is less than 1%. A consideration of the origin of a dielectric anisotropy suggests that the difference of approximately 0.0037 between the optical permittivity measured parallel and perpendicular to the c-axis exists in ice at frequencies less than 500 THz.
The plastic deformation resulting from a uniaxial compressive stress does not alter the permittivity and attenuation of ice at radio-frequencies. In view of the fact that the ice in naturally occurring masses is in a mechanically strained state, this conclusion confirms the present calculation of the depth of ice from radio-echo sounding.
Acknowledgement
We are indebted to Dr D. W. Davidson and co-workers of the National Research Council, Ottawa, for the loan of the RX-Meter and to Dr S. J. Jones of this laboratory for providing the single crystals of ice and for his help in examining the polycrystalline ice samples.






