1. Introduction
Calving of icebergs is an important mechanism for rapidly transferring mass from the polar ice sheets into the surrounding ocean. Recent observations have shown that changes in calving rate can greatly reduce the extent of floating ice shelves and ice tongues, potentially resulting in increased discharge from the interior (Reference Joughin, Abdalati and FahnestockJoughin and others, 2004; Reference Rignot, Braaten, Gogineni, Krabill and McConnellRignot and others, 2004). While the break-up of floating ice tongues has negligible direct effect on global sea level, the resulting speed-up of grounded ice can have major consequences for global sea level. Indeed, a wide range of observations applying to both current ice masses and palaeo-ice sheets point to iceberg calving as a major factor in rapid ice-sheet changes (Reference Van der VeenVan der Veen, 2002). Rapid changes in ice dynamics of Greenland outlet glaciers have been documented in a number of recent studies (Reference Thomas, Abdalati, Frederick, Krabill, Manizade and SteffenThomas and others, 2003; Reference Joughin, Abdalati and FahnestockJoughin and others, 2004, Reference Joughin2008a, Reference Joughinb, Reference Joughin, Das, King, Smith, Howat and Moonc; Reference Howat, Joughin, Tulaczyk and GogineniHowat and others, 2005, 2007, 2008b;Reference Luckman, Murray, de Lange and HannaLuckman and others, 2006;Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006;Reference Csatho, Schenk, van der Veen and KrabillCsatho and others, 2008;Reference Moon and JoughinMoon and Joughin, 2008). In particular, recent changes on Jakobshavn Isbræ on the west coast, and Helheim and Kangerdlugssuaq glaciers on the east coast have been detailed on seasonal timescales. Determining the most likely causes for recent behaviour of these outlet glaciers is crucial for assessing the future contribution of the Greenland ice sheet to global sea level. It is therefore important to formulate a calving model that can be readily incorporated into time-evolving numerical ice-flow models and, at the same time, is able to reproduce observed glacier behaviour. As a first step, the objective of the present study is to introduce a physically based calving model and to evaluate its impact on flow and dynamics of calving glaciers.
Calving criteria used in previous model studies fall into one of two main categories. The first type parameterizes the calving rate as a function of some independent variable such as water depth (Reference Brown, Meier and PostBrown and others, 1982; Reference Meier and PostMeier and Post, 1987; Reference Hanson and HookeHanson and Hooke, 2000), ice-front thickness (Reference PfefferPfeffer and others, 1997) or stretching rate (Reference AlleyAlley and others, 2007, 2008). The second approach specifies the position of the calving front, based on a height-above-buoyancy criterion, and the calving rate is then given by the rate at which ice is delivered to the ice front (Reference Van der VeenVan der Veen, 1996, 2002). Data collected on Columbia Glacier, Alaska, USA, prior to and during its rapid retreat and speed-up suggest that the position of the calving front is controlled by local geometry such that at the terminus the thickness in excess of flotation cannot become less than a certain threshold value (~50m for Columbia Glacier). Thus, for such height-above-buoyancy or flotation criteria the calving rate is not explicitly parameterized but is a result of flow and dynamics at the terminus. Inclusion of a flotation criterion in a numerical model reproduced unstable retreat through basal overdeepenings, and showed a more complex relationship between calving rate and water depth than assumed in earlier models (Reference Vieli, Funk and BlatterVieli and others, 2001; Reference Nick, van der Veen and OerlemansNick and others, 2007). A model incorporating the height-above-buoyancy criterion for calving was to some extent successful in explaining the recent retreat of Helheimgletscher, but could not reproduce the seasonal cycle of retreat and advance (Reference Nick, Vieli, Howat and JoughinNick and others, 2009).
A major difficulty with both the water-depth model and the height-above-buoyancy model is that these apply to grounded termini only. Moreover, these models produce inherently unstable glacier behaviour where the bed slopes downward towards the interior. A modest retreat of the calving front into deeper waters leads to further retreat that is halted only at the head of the fjord where the bed rises above sea level or where the bed slope reverses. Neither model can produce an advancing ice front without invoking other factors such as sedimentation at the terminus to reduce local water depth (Reference Nick, van der Veen and OerlemansNick and others, 2007, 2009). Most of the Antarctic marine-based glaciers and ice streams and many Greenland calving glaciers are buttressed by floating ice tongues or ice shelves from which icebergs are discharged. Thus, there is a need for calving models that can be applied to both floating and grounded ice fronts, and allow the calving front to advance on seasonal timescales, either by forming a short-lived floating ice tongue or by advancing a grounded terminus.
The model of Reference PfefferPfeffer and others (1997) calculated calving losses from a floating ice shelf as a nonlinear function of ice- front thickness, based on empirically determined fracture propagation rates. While having some physical basis, this model does not take account of key factors governing fracture location and extent (e.g. strain rate) and is only applicable to floating ice. Reference AlleyAlley and others (2008) also formulated a law for ice-shelf calving based on regression between stretching rate and velocity near the ice front, assumed to be closely approximating the calving flux. The implication of this model is that it tends to make ice shelves inherently unstable, whereby one calving event and associated terminus retreat leads to higher calving fronts, and consequently enhanced stretching, and could result in complete collapse. Because their regression is valid for near-steady termini, it is not immediately clear whether the model proposed by Reference AlleyAlley and others (2008) can be extended to rapidly retreating calving fronts. As is the case for the water-depth and height-above-buoyancy models, the physical underpinnings of the stretching-rate model remain tenuous at best.
The calving process is highly stochastic in nature, and may involve frequent detachment of smaller pieces from above or below the waterline, as well as more infrequent breaking of larger icebergs. Each calving event involves propagation of fractures, but considering local characteristics (e.g. shape of the snout, pre-existing planes of structural weakness, wave impacts) it is unreasonable to expect any model to be able to predict with any confidence when and where the next iceberg will break off. Nevertheless, it is possible to formulate a ‘bulk’ calving model that captures the main features of the average calving process that can be included in prognostic numerical ice-sheet models.
In an attempt to overcome limitations of existing calving models, Reference Benn, Hulton and MottramBenn and others (2007a, Reference Benn, Warren and Mottramb) introduced a calving criterion based on the depth of penetration of surface crevasses, which is in turn a function of longitudinal strain rates on the glacier tongue. The position of the calving front was defined as the point where crevasse depth equals the ice height above sea or lake level, based on the observation that many glaciers calve when crevasses reach the waterline, with failure of the subaerial part of the calving face followed after some interval by calving of the submerged superbuoyant ice toe (Reference MotykaMotyka, 1997). The waterline crevasse-depth criterion of Reference Benn, Hulton and MottramBenn and others (2007a, Reference Benn, Warren and Mottramb) has been incorporated into a three-dimensional (3-D), full-Stokes glacier model by Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others (2010). Their model could successfully predict ice-margin position for a specified glacier geometry, although glacier evolution through time was not investigated. Here we implement a modified crevasse-depth model in which the calving front is defined as the point where water-filled surface crevasses and basal crevasses penetrate the full thickness of the glacier. The waterline crevasse-depth model may be applicable to small, relatively slow tidewater glaciers such as those on Svalbard, whereas the modified model may be more representative of large, fast-flowing Greenlandic outlet glaciers. It must be emphasized that these models are not intended as literal representations of how individual calving events occur, but rather as a means of relating terminus position to ice dynamics in a simple but physically based way.
For tensile stresses of a few hundred kPa, air-filled crevasses extend to a depth of several tens of meters. However, where extensive surface melting takes place, existing surface crevasses can become water-filled, allowing further downward growth (Reference WeertmanWeertman, 1973; Reference Van der VeenVan der Veen, 1998b, Reference Van der Veen2007). Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others (2000) proposed that this mechanism explains how relatively minor changes in local climate conditions can lead to rapid disintegration of ice shelves. Similarly, Reference Sohn, Jezek and van der VeenSohn and others (1998) found seasonal variations in calving rate on Jakobshavn Isbræ associated with surface melting. Consequently, as suggested by Reference Benn, Warren and MottramBenn and others (2007b), the calving model presented here includes the effects of water on crevasse depth.
Prior studies on crevasse penetration (Reference SmithSmith, 1976, 1978; Reference Rist, Sammonds, Murrell, Meredith, Oerter and DoakeRist and others, 1996; Reference Van der VeenVan der Veen, 1998a,b) applied linear elastic fracture mechanics (LEFM) to estimate penetration depth of crevasses on glaciers. In that approach, the stress intensity factor is used to describe elastic stresses near the crevasse tip, thereby accounting for local stress concentrations promoting fracture growth. When compared to the fracture toughness of ice, the stress intensity factor provides a measure for how deep a crevasse can penetrate into the ice, if stresses acting on the crevasse are known. This approach, however, is not readily incorporated into numerical ice-flow models. Therefore, following Reference Benn, Warren and MottramBenn and others (2007b) the simplifying assumption is made here that crevasses propagate to the depth at which the tensile stress equals the lithostatic stress and the net longitudinal stress is zero (Reference NyeNye, 1955, Reference Nye1957). This simplification is appropriate because where crevasses are closely spaced, as is the case for most calving termini, stress concentrations at crevasse tips are small. Crevasse depths predicted by the zero-stress model are very close to those obtained by the LEFM approach for a field of crevasses (Reference Van der VeenVan der Veen, 1998b; Reference Mottram and BennMottram and Benn, 2009). The zero-stress condition allows crevasse penetration depth to be readily estimated anywhere in the terminus region and a simple calving criterion to be implemented into a time-evolving numerical model.
Our primary objective is to investigate whether the new calving model can generate realistic patterns of glacier advance and retreat, both long-term and on seasonal timescales, and how the bed topography influences flow dynamics and terminus stability. In order not to obfuscate interpretation of model results, processes that may force terminus migration are, in this study, limited to variations in water level in surface crevasses, in accumulation and in back pressure at the calving front. We are aware that other processes (e.g. basal melting under floating ice tongues) may play an important role in the control of the position of marine glacier termini, as highlighted by Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others (2008) for Jakobshavn Isbræ, and that they should be included in attempts to model observed behaviour of actual outlet glaciers.
In the following sections, we first describe the crevasse-depth calving model, and the ice-flow model used to evolve the glacier through time. The numerical model is then applied to an idealized geometry, to evaluate glacier response and stability to various imposed forcings. For comparative purposes, similar model runs were conducted using the waterline crevasse-depth model and a height- above-buoyancy calving criterion.
2. Calving Model
In a field of closely spaced crevasses, little tensile stress can exist within the thin slabs of ice separating adjacent crevasses, so there are no large stress concentrations near the tips of crevasses (Reference WeertmanWeertman, 1973). This suggests that under these conditions the depth of surface crevasses may be estimated following the model introduced by Reference NyeNye (1955, Reference Nye1957). That is, crevasses will penetrate to the depth at which the net longitudinal stress becomes zero. In the absence of water in the crevasses, at this depth the longitudinal tensile stress equals the compressive ice overburden pressure. The normal stress responsible for crevasse opening is the resistive stress, Rxx , defined as the full stress minus the lithostatic stress and related to the longitudinal stretching rate through Glen’s flow law (Reference Van der VeenVan der Veen, 1999, p.38),

where A is the temperature-dependent rate factor, n = 3 is the flow parameter, and the contribution of other strain rates to the effective strain rate has been neglected. The simplifying assumption is made that this stress is constant with depth (Reference Rist, Sammonds, Murrell, Meredith, Oerter and DoakeRist and others, 1996; Reference Van der VeenVan der Veen, 1998b). Allowance can be made for depth variation resulting from non-uniform temperatures throughout an ice column if, for example, stretching rate is considered independent of depth (Reference Van der VeenVan der Veen, 1998a). Such refinement will not, however, significantly alter the behaviour of the model glacier.
The lithostatic stress, or ice overburden pressure, increases with depth according to
where ρi is the ice density, g is the gravitational acceleration, H is the ice thickness and z is the vertical coordinate with z = 0 at the glacier or ice-shelf base. As noted by Reference Rist, Sammonds, Murrell, Meredith, Oerter and DoakeRist and others (1996), the density of near-surface firn is considerably lower than that of solid ice, thereby reducing the crevasse closing stress and allowing the crevasse deeper penetration than if constant density is assumed (cf. Reference Van der VeenVan der Veen, 1998b). We assume a constant value of ρi (920 kg m-3) corresponding to solid ice, which is probably realistic in glacier ablation zones (e.g. the termini of Greenlandic glaciers). We note, however, that density variations can be readily incorporated into the model.
Equating the tensile stress (Equation (1)) with the ice overburden pressure (Equation (2)) yields the penetration depth, d s, of surface crevasses (Reference NyeNye, 1955, Reference Nye1957),

The Nye model does not take into account the strength of ice and allows crevasses to exist for all values of the tensile stress. In reality, if the tensile stress is less than some threshold value, no crevasses will form. This condition is important in determining where crevasses will first form, but for the heavily crevassed terminus region just upstream of the calving front, where the tensile stress is likely to be greater than the threshold stress, this issue may be ignored (Reference Van der VeenVan der Veen, 1998b).
For a surface crevasse containing water, an additional opening stress allows the crevasse to penetrate deeper (Reference WeertmanWeertman, 1973; Reference Van der VeenVan der Veen, 1998b). If d w is the water height in the crevasse, this additional stress equals ρw gd w, where ρw represents the density of meltwater. The crevasse penetration depth may then be estimated from (Reference Benn, Warren and MottramBenn and others, 2007b)

In the initial form of the crevasse-depth model, the position of the calving front is defined as the point where d s equals the glacier freeboard above sea level, based on the observation that many subaerial calving events occur when the depth of surface crevasses approaches the waterline, followed by calving of the subaqueous toe (Reference MotykaMotyka, 1997). On the other hand, observations on Greenland outlet glaciers show infrequent calving of larger pieces or tabular icebergs interspersed with numerous smaller calving events (personal communication from L. Stearns, 2009). Production of these larger bergs likely involves full-thickness fracturing. Therefore we introduce a modification to the Reference Benn, Warren and MottramBenn and others (2007b) calving model, in which calving occurs when surface crevasses reach the depth to which basal crevasses penetrate upward into the ice. Significant upward propagation of basal crevasses is possible only where the glacier is at or near flotation and stretching rates are large (Reference Van der VeenVan der Veen, 1998a), so for grounded termini this implies that the water-filled surface crevasse must penetrate nearly the full ice thickness before a calving event occurs. On floating glacier tongues, however, basal crevasses can penetrate upward a significant fraction of the ice thickness, thus facilitating the calving process.
To estimate the height of basal crevasses, the net normal stress must be considered. This stress is the sum of the lithostatic stress, the pressure of water filling the crevasse, and the tensile stress associated with flow stretching. Adding these three contributing stresses yields (Reference Van der VeenVan der Veen, 1998a, Equation (16))
In this expression, σn is the net normal stress, z is the height above the glacier or ice-shelf base, H p is the piezometric head, or the height above the base to which water in a borehole to the bed will rise, and ρp is the density of sea or lake water (depending on the proglacial water body into which the glacier calves). For a floating ice tongue, the piezometric head corresponds to sea level. The assumption is made here that where the terminus is grounded, a full and easy connection between the subglacial drainage system and the adjoining sea or lake exists. In that case, H p equals the depth, D, of the glacier sole below sea level.
As in the case of surface crevasses, where basal crevasses are closely spaced, stress concentrations at the crevasse tips may be ignored and the penetration height may be estimated from the requirement that the net longitudinal stress is zero at that height (Reference WeertmanWeertman, 1980; Reference JezekJezek, 1984). After some rearranging, this gives

where H ab represents the height above buoyancy, defined as
For a floating ice tongue, H ab = 0, and the height of the bottom crevasses is determined solely by the tensile stress, R xx. On grounded glaciers, H ab > 0 and basal crevasses will penetrate less far upward.
The modified calving model is now complete. Because the depth of surface crevasses is estimated from the longitudinal stress and water level in the crevasses (Equation (4)), the model allows links between calving rate and changes in climate conditions to be explored. Water levels may be expected to increase during the melt season, starting from zero at the end of the winter, as surface meltwater collects in the crevasses. Progressive melting allows surface crevasses to penetrate deeper into the ice, thus providing a mechanism for increased calving losses during summer.
For the present applications, we do not specify surface melt and freezing rates, but rather prescribe directly water level within crevasses as simple forcing scenarios. In principle, though, water depths in crevasses could be modelled explicitly.
3. Ice-Flow Model
The calving model has been incorporated into a numerical ice-flow model that calculates the flow and geometric evolution, based on the model used by Reference Nick, Vieli, Howat and JoughinNick and others (2009). The ice-flow model is briefly outlined below. A list of model parameters and their values is given in Table 1.
Table 1. Values of model parameters

3.1. Continuity and force balance
Considering a flowband of width W and thickness H, conservation of mass is expressed by the depth-integrated continuity equation (Reference Van der VeenVan der Veen, 1999; Reference OerlemansOerlemans, 2001),

where t is time, x is the distance along the central flowline and a is the surface mass balance. Neglecting the effect of sloping side-walls, the horizontal ice flux through a cross section of the flowband is given by q = HWU, with U the vertically averaged horizontal ice velocity.
Conservation of momentum requires

where ν is the strain-rate dependent effective viscosity, defined as

Equation (9) states that the driving stress (right-hand side) is balanced by resistive forces associated with gradients in longitudinal stress (first term on the left-hand side), drag at the glacier bed (second term) and lateral drag (third term). The assumption is made that basal drag depends on sliding velocity and effective basal pressure (Reference BindschadlerBindschadler 1983; Reference Van der VeenVan der Veen and Whillans, 1996; Reference Vieli and PayneVieli and Payne, 2005). The sliding parameter, A s, and the friction parameter, μ, may be related to bed roughness and basal water, respectively. The value m = 3 is chosen for the nonlinear sliding relation. Resistance from drag along the lateral margins is estimated by integrating the force-balance equation over the width of the flowband assuming that lateral drag supports the same fraction of driving stress along a transect across the glacier (section 5.5 of Reference Van der VeenVan der Veen, 1999).
3.2. Boundary conditions
The up-glacier boundary, x = 0, corresponds to the ice divide where the surface slope and horizontal velocity are set to zero. At the calving front, the longitudinal stress is balanced by the difference between hydrostatic pressure of the ice and water, giving for the depth-averaged stress

in which D is the depth of the glacier base below sea level and σB is a back pressure from sea ice or sikkusak. Applying Glen’s flow law and rearranging, the corresponding stretching rate at the terminus is

The second boundary condition at the terminus is provided by the calving criteria discussed in section 2, to account for mass loss at the terminus. The crevasse-depth model allows formation of an ice shelf or a floating tongue when ice thickness is less than the flotation thickness. The transition between grounded ice and shelf is achieved through setting basal resistance to zero; that is, the friction parameter, μ, in Equation (9) is set to zero when the ice thickness becomes less than the flotation thickness.
In the crevasse-depth model, the local water depth or front geometry influences the glacier flow and strain rate and eventually calving rate. But, contrary to previous calving models, there is no direct dependency of calving rate on the water depth.
Model calculations are performed on a moving grid, which allows the glacier front to be followed continuously (Reference Nick and OerlemansNick and Oerlemans, 2006). The initial horizontal grid spacing is 300 m; this distance changes with every time-step as a new grid is defined to fit the new glacier length. For cases with a floating ice tongue, grounding-line motion has been checked for spatial grid-size independency by model experiments with refined grid resolutions. The problem of grid-size dependency (Reference Vieli and PayneVieli and Payne, 2005) is here overcome by the chosen high spatial resolution. Since basal resistance depends on effective basal pressure (second term in Equation (9)), it decreases as the ice thickness thins down to the flotation thickness. Therefore there is a smooth transition in basal resistance from the grounded to the floating ice tongue. Equation (9) is solved using a standard Newton iteration method. The fluxes and velocities are computed on a staggered grid between the gridpoints where thickness is calculated (more detail can be found in Reference Vieli and PayneVieli and Payne, 2005).
4. Model Experiments
Our objective here is to evaluate how different calving criteria affect glacier dynamics. In particular, we seek to explore how a floating ice tongue affects the stability of the terminus in the presence of a basal overdeepening and whether the flowline model can produce a seasonally advancing and retreating terminus in such a geometric setting. Three calving models are considered: (1) the crevasse-depth model (CD) in which a calving event occurs when the combined depth of surface and bottom crevasses equals the ice thickness; (2) the waterline crevasse-depth model (CDw), with calving occurring when a surface crevasse extends down to the waterline (Reference Benn, Warren and MottramBenn and others, 2007b);and (3) the height-above-buoyancy or flotation model (FL) in which the glacier thickness at the terminus cannot be less than a given limit, H c. Following Reference Vieli, Funk and BlatterVieli and others (2001), the critical thickness is defined as a small fraction, q, of the flotation thickness plus the flotation thickness:
At each time-step, the position of the terminus is shifted to the location where the thickness equals this critical thickness.
For the following model experiments and besides changing surface mass balance, the main forcing for terminus migration is through the variation of water level within crevasses, d w, or of back pressure at the calving front, σ B . These forcings reflect processes such as surface melt and the existence of sea ice or sikkusak and are both linked to climate and, to some extent, oceanic conditions. Our choice for the model forcing does not imply that these are the only important drivers for outlet glacier change. Indeed, observations indicate that other processes, such as changes in basal lubrication or oceanic melting beneath floating ice tongues or at the grounding line, may play an important role as control for calving-front dynamics (Reference Motyka, Hunter, Echelmeyer and ConnorMotyka and others, 2003, Reference Motyka, Truffer, Fahnestock and Luthi2009; Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008; Reference JoughinJoughin and others, 2008c). While such processes should be included in attempts to model realistic behaviour of actual outlet glaciers, our study represents a first step towards this objective. The limiting of forcing processes to variations in water level and in back pressure still targets our main aim of investigating the primary implications of calving criteria on marine outlet glacier dynamics on the relevant timescales.
An idealized geometry (Fig. 1) is used consisting of a wide accumulation area and a narrow outlet channel to the sea. Except near the ice divide, the bed is below sea level with two overdeepenings. The size of the model glacier is purposely kept small (total catchment area of ~100km2) to minimize possible stabilizing effects from increased discharge from the interior. For all three calving models, steady-state profiles were produced using parameter values given in Tables 1 and 2. The profile shown in Figure 1 corresponds to an initial glacier length of 46 km and was used as the initial geometry for modelling advance past the proglacial overdeepening. A second equilibrium profile with a glacier length of 69 km served as the initial profile to investigate glacier retreat (Fig. 4).

Fig. 1. Initial steady-state geometry: (a) glacier surface and basal elevation along the central flowline; (b) glacier width; and (c) annual surface mass balance.
Table 2. Overview of model comparison experiments for the three calving criteria

4.1. Terminus advance
In a first set of experiments for the CD and CDw models, glacier advance is forced by reducing the water level in surface crevasses (d w in Equation (4); see Table 2). For both the CD and CDw models, an ice shelf forms and the grounding line advances through the basal depression to reach a steady-state position just beyond the deepest point, on the upsloping bed (Fig. 2). In this particular model experiment, the grounding line does not advance all the way to the next bed high; by decreasing the crevasse water level further, advance to the next bed high occurs (not shown here). The FL model is forced by reducing the critical thickness (smaller value of q in Equation (14)), but it only produces minor advance and does not advance beyond the bedrock low, as was also found in earlier model studies (Reference Nick, van der Veen and OerlemansNick and others, 2007).
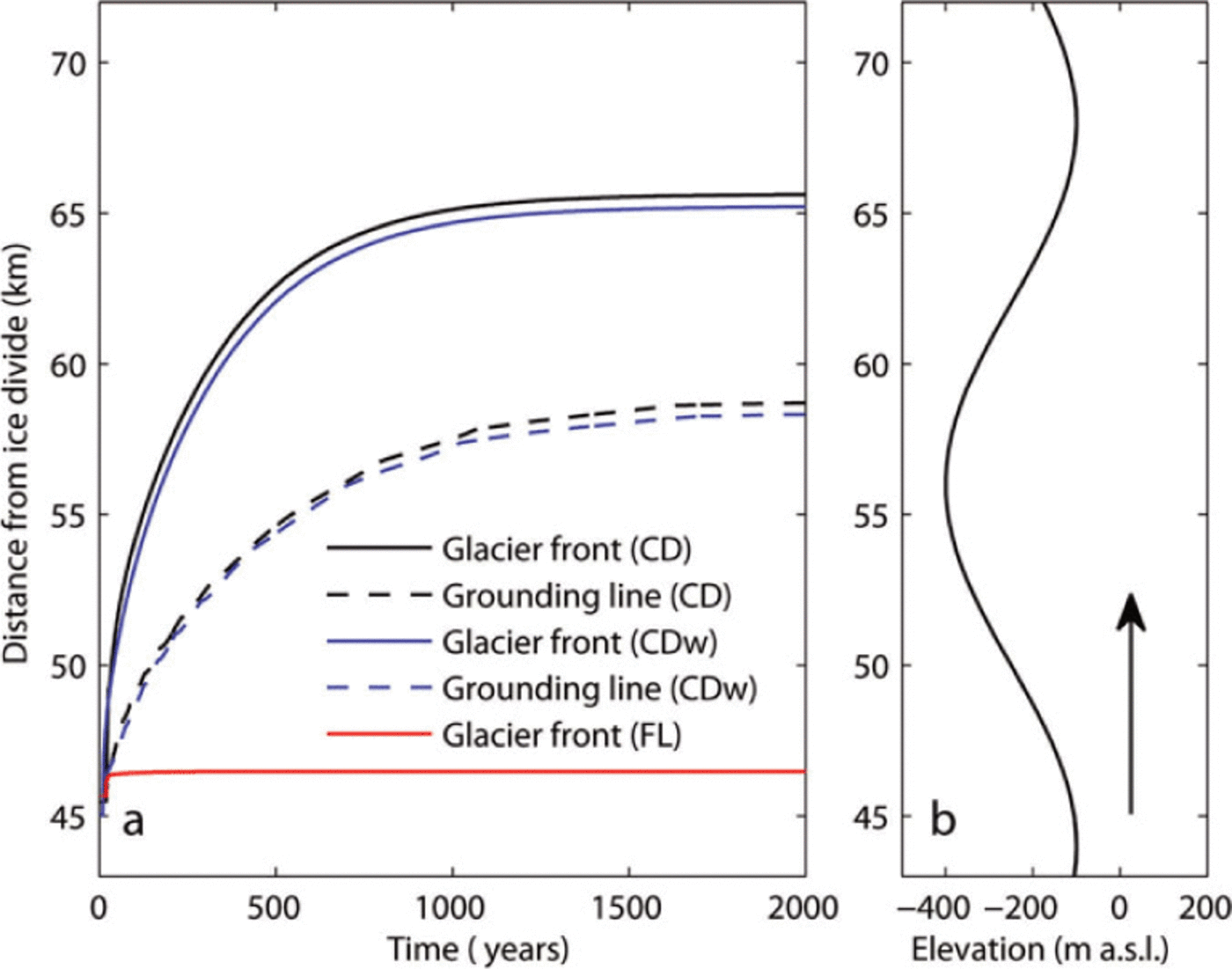
Fig. 2. The simulated advance forced by decreasing water level in crevasses or critical height. (a) Glacier length evolution in time for different calving criteria, the CD, CDw and FL models (black, blue and red, respectively). The black and blue dashed curves show position of the grounding line for CD and CDw models, respectively. (b) Bed elevation at glacier front. Arrow indicates direction of advance.
In a second set of experiments, glacier advance is achieved by increasing the accumulation rate in the catchment area (i.e. a in Equation (8) is doubled where a > 0). The terminus advances across the basal trough to the next basal high (Fig. 3). During the initial stage of advance into deeper water, a small ice shelf forms for the CD and the CDw model (Fig. 4). Again, in the FL model, increasing surface accumulation does not allow glacier advance into deeper water, even if an extreme increase (by a factor of 20) is applied.

Fig. 3. The simulated advance forced by an increase in the accumulation rate by factor 2. (a) Glacier length evolution in time for different calving criteria, the CD, CDw and FL models (black, blue and red, respectively). The black and blue dashed curves show position of the grounding line for CD and CDw models, respectively. The dashed red curve refers to the case in which an extreme increase in accumulation rate (by factor 20) is applied. (b) Bed elevation at glacier front. Arrow indicates direction of advance.

Fig. 4. The simulated surface profiles along the central flowline for experiment using the CD model and increased accumulation rate (corresponding to the black curve in Fig. 3). The time interval between the profiles is 50 years.
4.2. Terminus retreat
To investigate glacier retreat, model runs start from a steady-state glacier with a length of 69 km, similar to the most advanced profile shown further below in Figure 4. Model parameters used to obtain the initial profile are listed in Table 2.
Increasing the water level in crevasses results in deeper penetration and initially higher calving rates. For both the CD and CDw models, the terminus retreats a few kilometres behind the basal high before reaching a new equilibrium position on the upward slope (Fig. 5). Similar retreat results70 from a decrease in accumulation rate in the catchment basin (Fig. 6). For the FL model, any increase in critical thickness (Fig. 5) or decrease in accumulation rate (Fig. 6) moves the terminus over the basal high into the basal overdeepening where it retreats rapidly and is halted only when the terminus reaches the shallower bed. This unstable behaviour is the direct consequence of the terminus position being linked to water depth in the FL model.

Fig. 5. The modelled retreat forced by increasing water level in crevasses or critical height. (a) Glacier length evolution in time for different calving criteria, the CD, CDw and FL models (black, blue and red, respectively). (b) Bed elevation at glacier front. Arrow indicates direction of retreat.
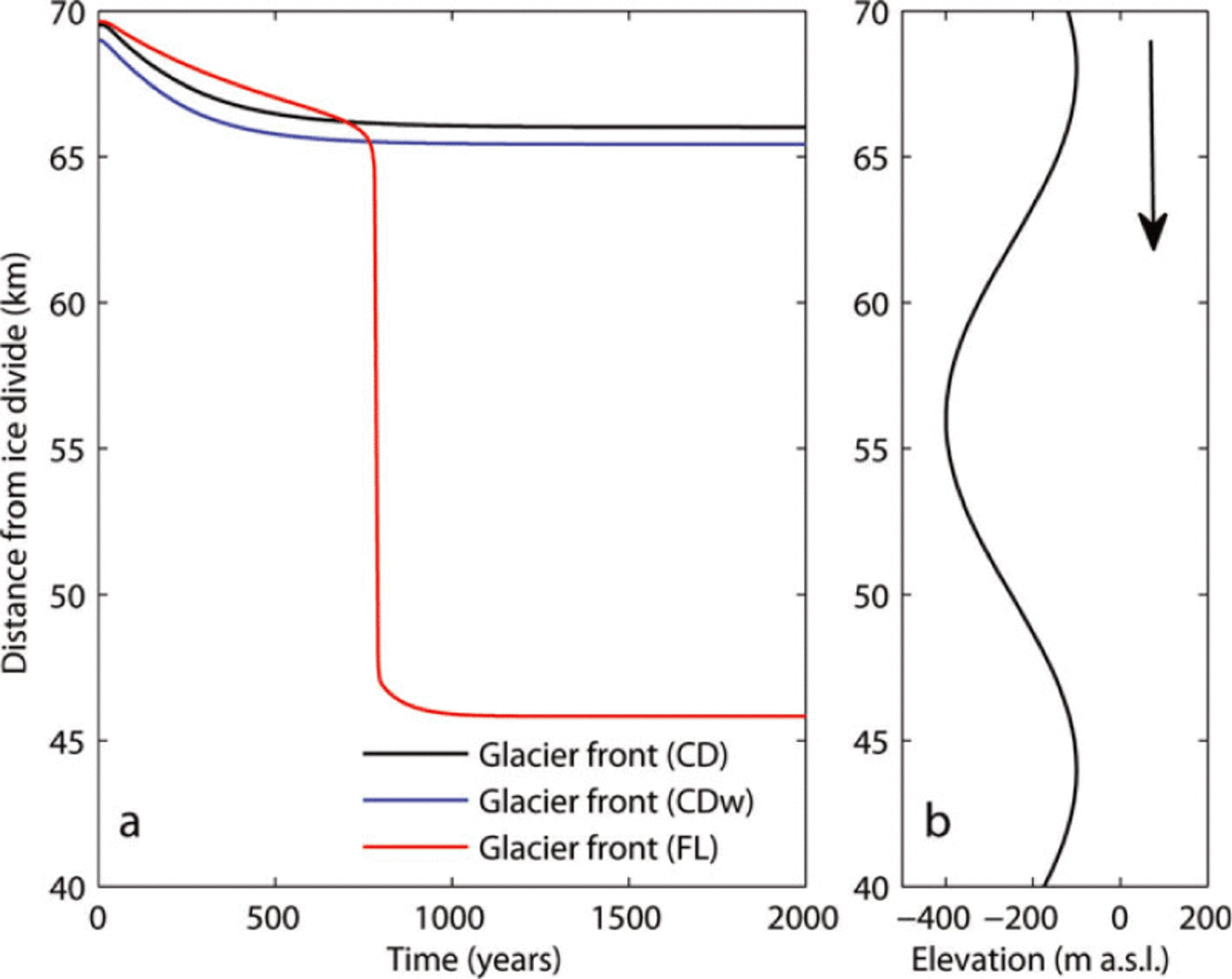
Fig. 6. The simulated retreat forced by a decrease in the accumulation rate by factor 0.7. (a) Glacier length evolution in time for different calving criteria, the CD, CDw and FL models (black, blue and red, respectively). (b) Bed elevation at glacier front. Arrow indicates direction of retreat.
To further illustrate the difference between the CD and FL calving criteria, Figure 7 shows retreat forced by a decrease in surface accumulation with a bed geometry characterized by a longer, deep basal depression. In the CD model, the glacier reaches a new equilibrium characterized by the presence of a small ice shelf (Fig. 8). Retreat is arrested well before the grounding line reaches shallower water. In contrast, the FL model predicts retreat all the way through the basal depression. Because terminus position in the FL model is directly linked to water depth, retreat does not stop until the calving flux reduces as it reaches the shallower bed.

Fig. 7. The modelled retreat on a bed geometry characterized by a long deep depression. Glacier retreat is forced by applying a decrease in the accumulation rate by factor 0.7. (a) The black and red curves indicate position of the glacier front for the CD and FL models, respectively. The dashed curve shows position of the grounding line for the CD model. (b) Bed elevation at glacier front. Arrow indicates direction of retreat.

Fig. 8. The simulated surface profiles along the central flowline for the experiment using the CD model and forcing a retreat by decreasing the accumulation rate by factor 0.7. The time interval between the profiles is 50 years.
4.3. Stability on a reversed bed
As shown in Figures 2 and 5, when using the CD or CDw model, the glacier can reach a steady state on an upsloping bed, which is not possible for the height-above-buoyancy model (Reference Vieli, Funk and BlatterVieli and others 2001; Reference Nick and OerlemansNick and Oerlemans, 2006). This is because in both the CD and CDw models, the calving flux is not directly related to water depth and terminus retreat into deeper water does not necessarily increase the calving flux. To investigate this issue further, the CD model is used starting from a steady-state geometry with a glacier length of 65 km and terminating on the upward bed slope shown in Figure 1a with a constant water level of 120 m in surface crevasses. Note that for this case no floating ice tongue occurs and the terminus is grounded. A step increase in water level by 5 m allows crevasses to penetrate deeper and a sudden increase in calving flux occurs, causing the terminus to retreat into deeper water (Fig. 9a and b). However, as the terminus retreats further, the calving flux does not increase accordingly and, in fact, decreases rapidly as the glacier front thickens (Fig. 9c). The retreat slows down and approaches a new equilibrium with the grounding line on the reversed bed. Note that for this experiment no floating tongue formed during retreat and the terminus position coincides with the grounding line. Glacier retreat first results in a step increase in speed (Fig. 9d) as resistive stresses are reduced, but the speed-up is short-lived and the velocity starts slowly decreasing again. This reduction in frontal velocity stabilizes ice discharge while the terminus thickens (Fig. 9e), which in turn slows terminus retreat. Figure 9f illustrates how the ice flux suddenly increases after increasing water level in the surface crevasses, but stabilizes shortly thereafter. In the new steady state, the ice flux at the terminus is greater than before the perturbation was imposed, to compensate for the loss of part of the ablation zone.

Fig. 9. Glacier retreat on an upsloping bed in response to a step change in water level in surface crevasses at time t = 10 years.
The important finding is that the terminus and grounding line stabilize on a reverse bed slope, even for the case where no floating ice tongue or ice shelf exists that could potentially impose a buttressing force due to lateral resistance. This contradicts common views regarding stability of marine-based glaciers. Also, the model results show that the system is sensitive to the formulation of the calving model.
The model results above and presented in Figures 2-8 show little difference in response between the calving model based on full thickness crevasse penetration (CD) and the model based on penetration to the waterline (CDw). When externally forced, both models predict grounding-line advance or retreat, with retreat not necessarily being unstable or controlled by the geometry of the bed. The height-above-buoyancy calving model cannot produce terminus advance over a deep basal depression, and retreat, once initiated, is halted only where the bed becomes sufficiently shallow. Consequently, the FL model cannot reproduce significant seasonal terminus advance and retreat as typically observed for Greenland outlet glaciers (Reference Howat, Smith, Joughin and ScambosHowat and others, 2008a,b; Reference JoughinJoughin and others, 2008c). In the following set of experiments, which explores the dynamic response to a seasonal forcing, we therefore only present results obtained from the CD model.
4.4. Response to seasonal forcing
Two types of seasonal forcings are imposed, namely a periodic change in water level in surface crevasses (representing simplified seasonal variations in surface melting and runoff), and a periodic change in the magnitude of back pressure at the glacier terminus (reflecting seasonal changes in the concentration of sea ice and sikkusak in front of the calving terminus).
The initial geometry for these experiments is the steady- state glacier with a length of 69 km, as in the retreat experiments shown in Figures 5 and 6. The model is then run for 200 years with seasonal forcing to reach a stable seasonal variation in terminus position. The results in Figures 10 and 11 show the last few years of this time integration.

Fig. 10. Seasonal glacier variation using the CD model. Modelled ice-front position (a) and ice velocity at different locations behind the ice front (b) for a seasonal variation in water level in surface crevasses (c).
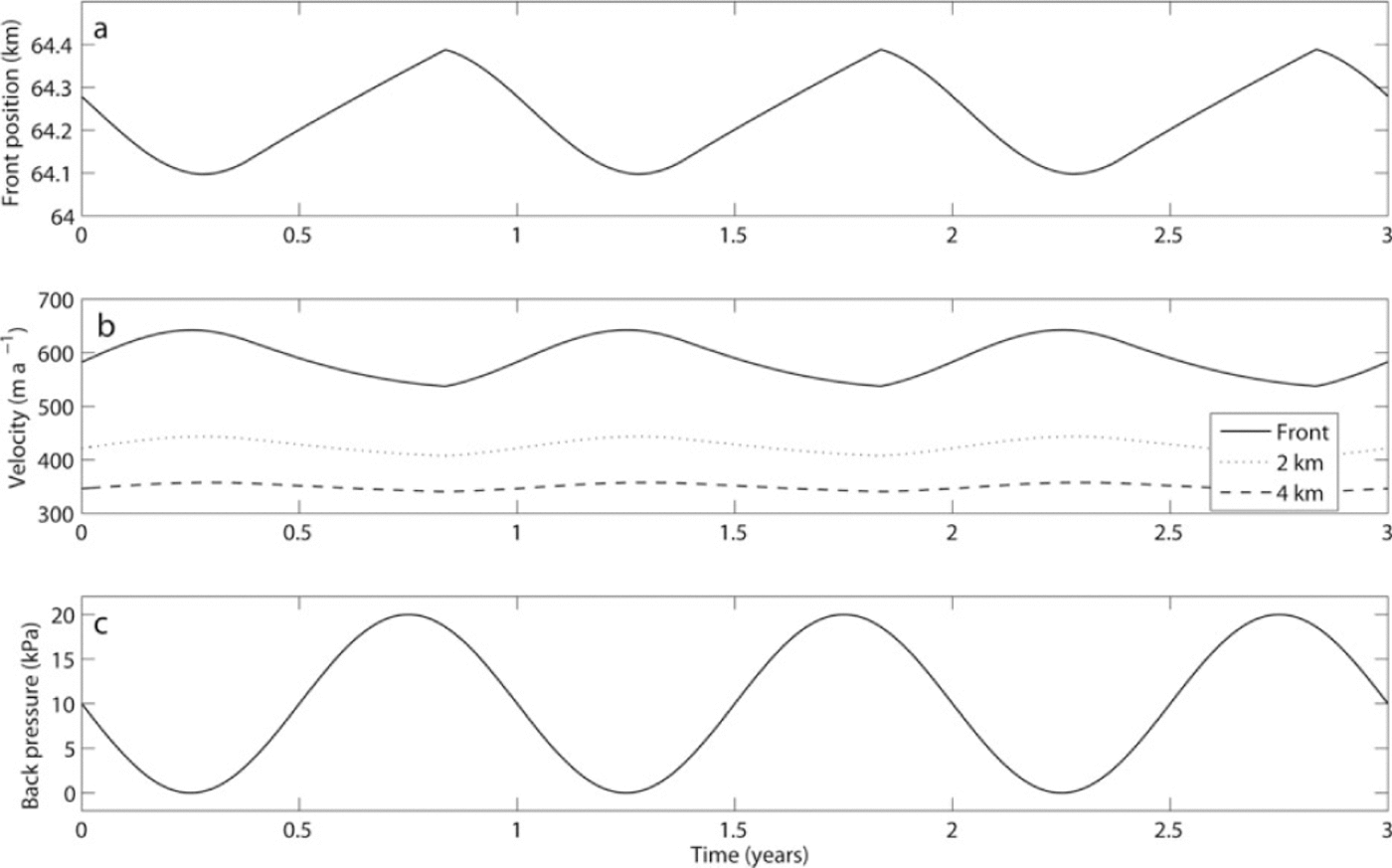
Fig. 11. Modelled ice-front position (a) and ice velocity at different locations behind the ice front (b) in response to a seasonal variation in back pressure at the glacier front (c).
We first consider the dynamic response to sinusoidal variations in water level of 20 m amplitude (Fig. 10c). Increasing the water level increases calving losses, forcing the terminus to retreat (Fig. 10a). Retreat continues until the water level starts decreasing and the terminus advances. During advance, calving goes almost to zero and the terminus advances with the speed of the glacier. Increasing the water level does not promptly result in a retreat; the glacier continues advancing until crevasse depth is sufficient to penetrate through the glacier thickness and then retreat is initiated. Associated with frontal advance and retreat are periodic changes in ice velocity (Fig. 10b), with velocity increases occurring simultaneously with terminus retreat as a result of reduced basal and lateral resistance and greater frontal height. Speed variations are greatest at the terminus and are rapidly muted upstream of the calving front (Fig. 10b).
Confining sikkusak in front of the terminus may exert a back pressure on the glacier front (Equation (12)). As the sea- ice concentration reduces during the summer, this back pressure may be expected to decrease. Again, a sinusoidal seasonal variation is imposed with 20 kPa amplitude (Fig. 11c), resulting in cyclic response of terminus position (Fig. 11a) and glacier speed (Fig. 11b). An increase in back pressure lowers the stretching rate at the terminus and results in shallower crevasse depths and lower calving rates. Conversely, reducing or eliminating the back pressure causes stretching rates to increase with deeper penetration of surface crevasses and including terminus retreat. The change in back pressure adopted here (20 kPa) may be unrealistically large, although the observation that confining sea ice may halt the rotation of large icebergs (Reference Amundson, Fahnestock, Truffer, Brown, Luthi and MotykaAmundson and others, 2010) suggests an appreciable back pressure from sikkusak in Greenlandic fjords. Adopting a significantly smaller change in back pressure does not produce a clear seasonal glacier response.
Comparison of the results shown in Figures 10 and 11 shows that seasonal variations in water level and in back pressure produce more or less the same dynamic glacier response. The glacier responds dynamically to short-term fluctuations in climate, as has been observed for some outlet glaciers in Greenland with ~15% seasonal change in velocity (e.g. Reference Luckman and MurrayLuckman and Murray, 2005; Reference JoughinJoughin and others, 2008c). It is worth noting that in these experiments no floating ice tongue forms during seasonal advance, indicating that the presence of such a tongue is not a necessary requirement for terminus advance.
5. Discussion
The model experiments described above show that crevasse-depth calving criteria allow a greater range of glacier behaviour to be modelled than has hitherto been possible. By allowing the formation of a floating ice tongue, the model can simulate glacier advance into deep water, unlike water- depth and height-above-buoyancy calving models which necessarily apply only to grounded termini (Reference Vieli, Funk and BlatterVieli and others, 2001; Reference Nick, van der Veen and OerlemansNick and others, 2007, Reference Nick, Vieli, Howat and Joughin2009). For the height-above-buoyancy model (as well as for the water-depth model; those results are not shown here), the model results suggest that retreat into deeper water, once initiated, is sustained by increased calving until the terminus reaches water depths sufficiently small to reduce calving and arrest the terminus (Figs 5-8). Subsequent terminus advance through deeper water is not possible (Figs 2 and 3) unless sedimentation at the grounding line is invoked to reduce the local water depth at the terminus, lowering calving rate (Reference Nick, van der Veen and OerlemansNick and others, 2007). This inherently unstable behaviour is eliminated by implementation of crevasse-depth calving criteria. Lowering the calving rate by decreasing the amount of water in surface crevasses or increasing accumulation in the catchment area allows an ice shelf to form and the grounding line to advance into or across a basal deepening (Figs 2-4). Increasing the calving rate or lowering accumulation forces the terminus to retreat, but this retreat is halted well before the terminus retracts to an upward slope (Figs 5 and 6).
Our model results indicate that the retreat and advance of calving outlet glaciers is not simply dictated by the bed topography. According to earlier results (e.g. Reference Vieli, Funk and BlatterVieli and others, 2001; Reference Nick, van der Veen and OerlemansNick and others, 2007, Reference Nick, Vieli, Howat and Joughin2009), terminus retreat into deeper water is irreversible and will be halted only where the bed becomes shallower. The main reason for this difference is that the current model eliminates any direct dependence of calving rate on the local water depth or ice thickness, and allows the system to respond to a broader range of climatic, topographic and glaciological controls.
Another feature of the new calving model is that it allows calving rate to be linked to seasonal variations in air temperature or surface melting. This, in turn, results in seasonal advance and retreat of the glacier terminus, as has similarly been observed on Greenland outlet glaciers. In the present simulations, seasonal variations in the amount of water in crevasses and in back pressure are prescribed directly, rather than these parameters being linked to climate parameters such as air temperature and temperature of the water in the fjord. This allows for a straightforward evaluation of model sensitivity. Nevertheless, for future studies, more realistic parameterizations or explicit modelling is appropriate. For example, there is a time lag between minimum sea-ice concentration and maximum air temperature, and the amount of sea ice formed during the winter will have an impact on concentrations during the following summer (Reference Gough and HouserGough and Houser, 2005). Our estimate for the back pressure on the glacier terminus due to the presence of confining sikkusak is based on observed seasonal changes in stretching rate at the terminus of Helheimgletscher (Reference Howat, Joughin and ScambosHowat and others, 2007, Fig. 2b). A more quantitative assessment is desirable when attempting to model observed behaviour more closely. Similarly, surface ablation likely depends on factors other than air temperature, such as previous snowfall, cloudiness, incoming solar radiation, etc.
Further, oceanic melt at the calving face and beneath floating ice tongues or ice shelves has purposely not been considered in this study, but observations suggest that it may play a crucial role in forcing marine outlet glacier change (Reference Motyka, Hunter, Echelmeyer and ConnorMotyka and others, 2003, Reference Motyka, Truffer, Fahnestock and Luthi2009; Reference Thomas, Abdalati, Frederick, Krabill, Manizade and SteffenThomas and others, 2003; Reference Shepherd, Wingham and RignotShepherd and others, 2004; Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008). Within the present model, basal melt can easily be included as a forcing process beneath the floating part and should certainly be considered and explored for realistic numerical models of marine outlet glaciers. Recent studies indicate that an accurate knowledge of the magnitude and more importantly the spatial pattern of basal melt is crucial for understanding its effect on the grounding-line dynamics (Reference Walker, Dupont, Parizek and AlleyWalker and others, 2008; O. Gagliardini and others, unpublished information), but our current understanding of basal melt processes is limited and prognostic models are in their infancy.
It must be repeated that the crevasse-depth calving criteria are not intended to represent the exact physical processes underpinning individual calving events. Calving occurs through a wide range of mechanisms, and the propagation of surface and basal crevasses in response to longitudinal stretching should only be regarded as a large-scale, first- order control on the position of the calving front (Reference Benn, Hulton and MottramBenn and others, 2007a). Similarly, our approach to modelling the overdeepening of water-filled crevasses must be regarded as a simplification of complex processes. However, by relating the position of calving fronts to crevasse depths, our model provides a way of linking calving losses to ice dynamics and surface melting in a physically plausible but workable way, unlike previously used calving criteria which rely on poorly tested empirical relationships.
Data presented by Reference Mottram and BennMottram and Benn (2009) show that the function for calculating the depth of dry crevasses (Equation (3)) yields reasonable results. However, to our knowledge, no equivalent data are available for water-filled crevasses, or the way in which crevasse depths vary throughout the year. Obtaining accurate field observations of crevasse depths is not an easy undertaking, so it will be very difficult to obtain direct observations that could be used to test our hypothesis that surface melt rates exert a direct control on calving losses by deepening surface crevasses. However, some indirect validation is provided by a rough agreement of model behaviour with observations on marine outlet glaciers, particularly their seasonal fluctuations in terminus position.
Calving is, of course, a 3-D process, and calving events require both lateral and vertical propagation of fractures. Such effects are not taken into account in our present model, which only considers fractures in two dimensions. A future goal, therefore, is the development of a full, 3-D, time-evolving calving model. On the basis of our modelling studies to date, we believe that crevasse-depth calving criteria provide the most promising means of representing the calving process in such models (Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010).
The current model experiments apply to an idealized geometry and employ a limited range of input variables, in order to investigate how the new calving criterion affects glacier dynamics and behaviour. The next step should be to apply the model to actual geometries of Greenland outlet glaciers (e.g. Helheimgletscher or Jakobshavn Isbræ) and simulate observed temporal variations more closely. Such validation will be crucial and should be possible with the much increased spatial and temporal resolution of flow velocity, front position and thickness observations that are becoming available from remote-sensing and field-monitoring programmes. Modelling exercises such as that reported in this paper can play an important role in guiding data collection, by highlighting which variables could be controlling observed behaviour. Taken together, model simulations and observations may provide important insights into the relative importance of different forcing processes and feedback mechanisms, and allow us to make further significant progress on the long-standing ‘calving problem’.
6. Concluding Remark
The main conclusion that can be drawn from the model experiments described in this contribution is that the choice of calving model in numerical prognostic ice-flow models crucially determines behaviour and stability of the model glacier. This means that better understanding of processes controlling calving from grounded and floating termini is needed. Observations to validate proposed models are needed, in particular seasonal progression of crevasse depths following the onset of surface melting, but also the inclusion of oceanic processes such as basal melt.
Acknowledgements
This paper is published with the permission of the Geological Survey of Denmark and Greenland. The research was funded mainly by the Danish Ministry of Climate and Energy through the Programme for Monitoring the Greenland Ice Sheet (PROMICE), by the UK Natural Environment Research Council (NERC) New Investigators Grant NE/E001009/1, and in part by US National Science Foundation grants ANT- 0424589 and ARC-0520427 (University of Kansas) and the ice2sea project funded by the European Commission’s 7th Framework Programme through grant No. 226375. F.M.N. is grateful for comments by H.M. Nick and D. van As, who helped to improve the model.














