List of Frequently used Symbols
(Units and additional symbols are defined in the text.)
Physical
ABL Atmospheric boundary layer
AWS Automatic weather station
C H, E Respective bulk-transfer coefficients for sensible heat and water vapour
C P Specific heat of air at constant pressure
e a Vapour pressure of air
e s Surface vapour pressure
k Von Ka´rma´n’s constant
K b Background turbulent exchange parameter
K kat Katabatic bulk exchange parameter
L Monin-Obukhov stability length scale
LV Latent heat of vaporization
Pr Turbulent Prandtl number
Q E Energy flux density due to water vapour
Q H Energy flux density due to sensible heat
T a Air temperature
T s Surface temperature
uz Wind speed at z
u* Friction velocity
z Measurement height above surface
z 0, H, E Respective roughness lengths for wind speed, temperature and humidity
γ Potential temperature lapse rate
ρ Air density
ΨM, H, E Respective stability corrections for wind speed, temperature and humidity
Statistical
d 2 Willmott’s index of agreement
N Sample size
Oi ith value of N observations (independent in regression)
Pi ith value of N predictions (dependent in regression)
r 2 Coefficient of determination in regression
rmse Root-mean-square error
rmseS Systematic root-mean-square error
rmseU Unsystematic root-mean-square error
X Independent variable in regression
Y Dependent variable in regression
α Intercept in regression
β Slope in regression
Overbars denote mean values ![]()
1. Introduction
Spatially distributed melt modelling of glacier surfaces poses the challenge of finding the extent to which physical detail can be applied to surface energy supply processes. Given the ability to calculate slope, azimuth and horizon values from a digital elevation model (DEM), it is reasonably straightforward to map incoming short- and longwave radiation in a physically complete way. However, the DEM does not provide the details required for physically sophisticated mapping of the turbulent energy supply, so the alternative of finding a suitable parameterization scheme is explored.
In view of the knowledge that katabatic winds are well developed during the glacier melt season, Reference Oerlemans and GrisogonoOerlemans and Grisogono (2002) used experimental data from Pasterzen-kees, Austrian Alps, to calibrate a katabatic bulk-exchange parameter, K kat:

which has the dimensions of a conductance (ms–1). The flow is forced by ΔT, the glacier air-surface temperature difference, where g is the acceleration due to gravity, T 0 the Kelvin surface temperature, γ a potential temperature lapse rate, κ the product of an empirically derived set of constants, and Pr the turbulent Prandtl number. K kat, referred to herein as the OG (for Oerlemans and Grisogono) parameterization, replaces the wind speed and surface drag coefficient in the classical bulk-transfer equations for heat transfer (e.g. Reference OkeOke, 1987), thus reducing the problem to one of representing the temperature field over the glacier and including a background turbulent exchange coefficient to allow for turbulence generated by the large-scale wind field (e.g. Reference Klok and OerlemansKlok and Oerlemans, 2002).
As noted in Reference Oerlemans and GrisogonoOerlemans and Grisogono (2002), there is a problem in validating the scheme using glacier automatic weather station (AWS) datasets because if temperature data near the glacier surface are used to estimate ΔT, the values are compromised by the cooling effect of the glacier. One must also consider that the application of classical bulk-transfer theory to glacier AWS data is theoretically weak in katabatic flow at any appreciable distance above the surface (Reference Grisogono and OerlemansGrisogono and Oerlemans, 2001, Reference Grisogono and Oerlemans2002), thus limiting its usefulness as a standard for validation. However, the goal of this paper is not to address weaknesses in the bulk-transfer approach or in the parameterization scheme. Rather, it is to assess the degree to which the two may converge when each is driven by an independent data source: a glacier AWS for bulk transfer, and an off-glacier AWS for the OG parameterization.
2. Measurements and Data
Peyto Glacier (51°40′ N, 116°33′ W) today occupies an area of approximately 13 km2, which is smaller than the area of Morteratschgletscher, Switzerland (≈17km2), and smaller still than that of Pasterzenkees (≈20km2). Peyto Glacier is similar to the other two in having a relatively extensive upper basin area and being surrounded by high mountains. The glacier elevation rises to approximately 3000 m around the upper limits of the accumulation zone and falls to 2100 m at the terminus, across a distance of approximately 5 km. AWS sites equipped with data loggers (Model CR10/10X, Campbell Scientific, USA) store hourly averages of meteorological measurements throughout the year. Data have also been obtained for short micrometeorological measurement periods during the melt season, also using data loggers (Model CR10/21X, Campbell Scientific, USA).
2.1. Automatic weather stations
The first AWS was installed off the glacier in the Geological Survey of Canada (GSC) base camp, at 2240 m a.s.l. and approximately 500m to the north of the glacier margin. The sensor complement of the station has gradually evolved over the 15 years that the station has been in operation, collecting hourly data throughout the year. To focus on the measurements which are relevant to this discussion, those of the past 3 years, an aerovane (Model 05103, R.M. Young, USA) is mounted 5m above the ground to measure wind speed and direction, while a Vaisala sensor (Model HMP35, Campbell Scientific, USA) is mounted 2m above the ground inside a Meteorological Service of Canada (MSC) shelter to measure temperature and relative humidity. These constitute the off-glacier data.
An examination of the summer (1 May–30 September) off-glacier wind direction record, for air temperature above 0°C (Fig. 1), shows that the wind is predominantly from the up-glacier direction. The small number of opposing directions usually occur during short periods of rainy weather, in association with low clouds and northeasterly winds. There is little indication of a diurnal rhythm in the wind direction during fair weather, such as might be expected if the station were sensing the anabatic and katabatic parts of the valley breeze cycle. Thus, although the off-glacier AWS is located 100m above the glacier tongue, its wind direction may be influenced by the glacier wind throughout the day. It should be noted too, however, that the glacier is located within the westerlies, in an area where local topography tends to direct the background flow along the orientation of the glacier tongue.

Fig. 1. Hourly wind direction at the Peyto Glacier base-camp AWS on summer days when air temperature is above 0°C.
The summers of 2001, 2002 and 2003 correspond to periods when useful glacier data were obtained from a year-round AWS located on the glacier tongue, approximately 1 km south of the base-camp AWS at an estimated elevation of 2170m. Here there are hourly measurements of wind speed, from an anemometer (Model 014A, Campbell Scientific, USA) mounted approximately 3m above the ice, and of temperature 2.25 m above the ice surface. The station has a floating design, with sensor heights selected to remain clear of the winter snowpack and to ensure unobstructed airflow around the anemometer. The record from an acoustic depth sensor (Model SR50, Campbell Scientific, Canada) drilled into the ice is used to correct sensor heights for snow depth. In selecting for the number of hours during which air temperatures at both AWS sites were above 0°C, more than 50% of a potential 3672 hours of data for each summer were obtained.
Air temperature was measured throughout each summer, using a thermocouple mounted inside a simple four-plate shield (Reference SchwerdtfegerSchwerdtfeger, 1976). A replacement sensor for measuring both temperature and humidity (Model CS500 with shield, Campbell Scientific, USA) was installed in 2003. A regression of thermocouple temperature, Y, against that of the replacement sensor, X, yields Y\1.05X-0.15°C (r 2 = 0.98), where the intercept is small enough to ignore and the slope is attributed to the fact that the replacement sensor was mounted 0.2 m below the level of the thermocouple so that they would not interfere with each other. Hence, the new sensor replaces the old in the temperature dataset at the time of installation, with sensor height adjusted accordingly.
Although the original intention was not to explore humidity until more data had been gathered, the 2003 record produced interesting results, so it is included. It was found, however, that relative humidity from the Vaisala probe would achieve maximum values of 100%, more or less, while those of the CS500 would maximize in the low nineties. This was interpreted to be a sensitivity problem, which was resolved by applying a multiplier of 1.07 to the CS500 data, thus allowing its readings also to maximize at approximately 100%. Station vapour pressures were calculated as the products of relative humidity and saturation vapour pressure, where the latter is empirically obtained from air temperature (e.g. Reference OerlemansOerlemans, 2000).
Despite the predominance of up-glacier wind directions in the off-glacier AWS record, the association between off-glacier speeds and those recorded on the glacier is not good (Fig. 2a). The two are positively and somewhat closely related, particularly through a corridor of values which seems to stand out in the data, where Y≈1.5X. Such a corridor may signify the best to expect if katabatic forcing of the glacier surface wind field is weak in comparison to forcing from the geostrophic flow aloft, but otherwise there is too much scatter to suggest that it would be a good strategy to scale the glacier wind field solely according to off-glacier wind-speed data. Hence, interest in the OG parameterization deepens, particularly if stronger associations can be found for the air-surface temperature difference, T a — T s, and the air-surface vapour-pressure difference, e a — e s, where T s and e s are at their respective melting-point values, 0°C and 610.8 Pa.
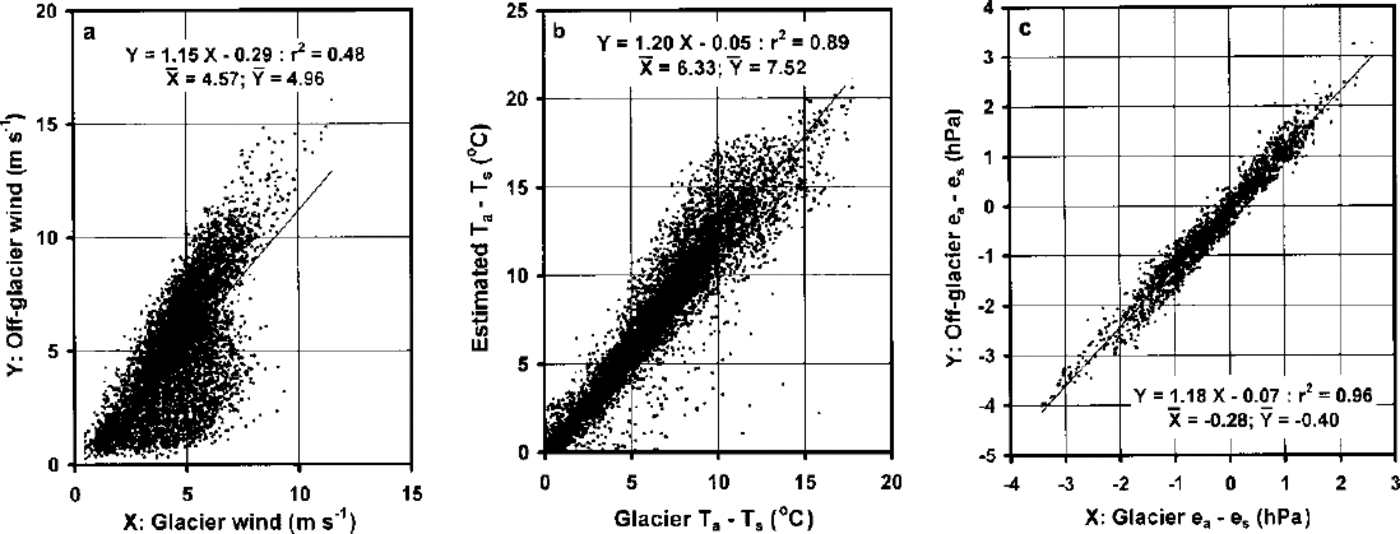
Fig. 2. Off-glacier AWS data compared with glacier AWS data for (a) wind speed, (b) temperature, T a, and (c) vapour pressure, e a, where T s refers to 0°C, and e s to 610.8 Pa.
Plots of T a — T s and e a — e s (Fig. 2b and c) estimated from off-glacier AWS data against those measured at the glacier AWS indicate close correspondences between the two sets of values. If one interprets the intercepts of best-fit lines to temperature and humidity as being sensitive to the lapses of environmental temperature and pressure with elevation, they are consistent with the small elevation difference between the two stations. Interpreting the intercepts in this way suggests that the slope of the temperature plot (Fig. 2b) depends upon the glacier surface cooling effect. Then, noting that relatively warm air above the katabatic layer is also likely to be relatively moist, the slope of the vapour-pressure plot (Fig. 2c) suggests a glacier drying effect.
Such interpretations are interesting to consider for modelling purposes, bearing in mind the risk of oversimplification (e.g. setting the environmental lapse rate to -0.00658Cm–1 despite the fact that it is known to vary over time and, more specifically, over small glaciers and ice caps (Reference Van den BroekeVan den Broeke, 1997b; Reference OerlemansOerlemans and others, 1999)). Atmospheric soundings were not available for this study, but those obtained over Pasterzenkees (Reference Van den BroekeVan den Broeke, 1997a, Reference Van den Broekeb) indicate a glacier atmospheric boundary layer (ABL) which is dryer and cooler than the air above, and that the cooling effect is limited to the first 100 m above the surface. In fact, Reference Greuell, Knap and SmeetsGreuell and others (1997) indicate that the cooling effect of Pasterzenkees is principally within the first 50m above the ice surface. Because the Peyto off-glacier AWS is at least 100 m above the glacier terminus, it seems reasonable to accept its data as being independent of the glacier ABL.
2.2. Micrometeorological measurements
Small micrometeorological datasets were collected in association with other work ((Reference MunroMunro, 1990; Reference Cutler and MunroCutler and Munro, 1996)), prior to the establishment of the glacier AWS (Table 1). The ‘robust’ instruments in Table 1 are the same types used for the glacier AWS in 2001, 2002 and 2003, the exceptions being a lighter wind sensor (Model 03001, R.M. Young, USA) for the upper measurement levels in 1988 and 1990 and thermistors (Model 107, Campbell Scientific, USA) at the lower measurement levels in 1988. The ‘sensitive’ instruments are light cup anemometers (Model 106, Thornthwaite Associates, USA) and a forced ventilation, double-shielded thermometer system, where thermocouples are embedded within metal rods which replicate the dimensions of standard MSC glass thermometers. Standard or manufacturer-supplied calibrations were used for all sensors.
Table 1. Micrometeorological datasets

The interesting feature of the micrometeorological data-sets is that the measurement levels encompass those which currently apply to the glacier AWS (Fig. 3). Because a range of mean wind speeds and temperatures applies to these data (Table 1) they have been normalized with respect to the averages of the 1 m wind speeds and temperatures, a convention which draws attention to the shapes of the 1994 profiles, i.e. how closely they approach the 4 and 5m height plots from the other sets. Although three different anemometer and thermometer designs are involved, the results are in broad agreement. The observation that the 4m wind speeds for 1990 stand out from the 5 m speeds of 1988 is consistent with the expectation of a steeper gradient for the stronger winds of that year (Table 1). The fact that the whole 1994 profile appears to be somewhat slow in relation to the 1 m level caused adjustments to the data to be considered. However, the decision was made to work with data as they are, so as to prevent corrections from being applied to some datasets but not to others.

Fig. 3. Wind speed (open circles) and temperature (solid circles) above ice or snow cover on Peyto Glacier, normalized according to 1 m averages across the datasets listed in Table 1. Power-law fits to the 1994 profiles are plotted as visual guides.
The wind-speed averages in Figure 3 agree with previous findings on Peyto Glacier (Reference Munro and DaviesMunro and Davies, 1977; Reference Stenning, Banfield and YoungStenning and others, 1981) and Pasterzenkees (Reference Van den BroekeVan den Broeke, 1997a, Reference Van den Broekeb) in suggesting that the glacier wind achieves maximum speed at heights close to 6m because there is very little change above 5m. As the cited works indicate, the height of maximum wind speed for any individual profile may be substantially lower or higher than 6m, thus contributing to variance in computations made from the data. It is also interesting that the ratio of the 6 and 2m average temperatures in Figure 3 is approximately 1.2, the same as the slope of the best-fit line in Figure 2b. This may be cause to reconsider the independence of the off-glacier AWS, except that most of the cooling effect occurs in the lower layers of the glacier ABL (Reference Van den BroekeVan den Broeke, 1997b) and, in any event, the datasets used in Figures 2 and 3 do not coincide.
The question remains as to how to use glacier AWS data to assess the OG parameterization because the glacier data are gathered above 1 m, the level where a stability-corrected bulk-transfer procedure is known to work well for this site (Reference MunroMunro, 1989, Reference Munro1990). A key assumption of the procedure is flux constancy with height, an assumption that is untenable in katabatic flow except, perhaps, in that part of the glacier ABL immediately adjacent to the surface (Van der Avoird and Duynkerke, 1999; Reference Oerlemans and GrisogonoOerlemans and Grisogono, 2002). Nevertheless, because the glacier AWS data available here apply to the first 2–3m of the glacier ABL, and the use of bulk-transfer theory appears to be fairly robust through much of the zone approaching the maximum katabatic wind-speed level (Reference Denby and GreuellDenby and Greuell, 2000), the decision was made to explore its potential for providing turbulent heat-transfer estimates against which to compare values that are parameterized from off-glacier AWS data.
3. Main Theoretical Points
3.1. Transport equations
The flux densities of sensible heat, Q H, and latent heat due to vapour exchange, Q E, over melting snow and ice are yielded by the bulk turbulent transfer expressions:

in which ρ is the air density, c p the specific heat of air at constant pressure, ε the gram molecular weight ratio of water to air, LV the latent heat of vaporization, and p the air pressure. The height, z, for wind speed, uz , is the measurement level for air temperature, T a, and vapour pressure, e a, while T s and e s are the surface values. On a melting surface it is assumed that LV = 2.5 × 106 Jkg–1, while the constants, c p and ε take their usual values (e.g. Reference OkeOke, 1987). Standard sea-level values of ρ and p are scaled according to elevation.
3.2. Bulk-transfer coefficients
The bulk-transfer coefficients for sensible- and latent-heat exchange, respectively C H and C E, are sensitive to stability and surface roughness:

where k is von Ka´rma´n’s constant (≈0.4). The stability corrections, ΨM, H, E, for wind speed, temperature and humidity, respectively, and the corresponding surface roughness lengths, z 0, H, E, can all be viewed as dynamic variables which are shaped by the properties of the flow, though z0 will here be taken as a constant. In neutral conditions, ΨM, H, E = 0 and Equation (4) reverts to a simple logarithmic form in which z H and z E are the only dynamic variables.
There is extensive literature on correction procedures for stable boundary layer flow, where ΨM, H, E > 0. This has recently been reviewed by Reference AndreasAndreas (2002), from which two approaches are extracted for use here. Both are based on the Monin-Obukhov stability length scale, L, which is practical to use over melting ice and snow:


where u * is the friction velocity and T is the Kelvin temperature of the air layer adjacent to the surface. The practicality stems from the fact that Q H is readily calculated, where T s = 0°C, because L can be obtained through iteration, given a suitable Ψ M function. Two such functions are used here, the first being the basis for the log-linear (LL) formulation which seems to work well for L>z (Reference Webb and MeteorolWebb, 1970),
and the second being a formulation due to Holstag and de Bruin (1988) (HB) which, when integrated with height (Reference LauniainenLauniainen, 1995), yields
Equation (6) is assumed to work within a similarity framework, such that ΨM = Ψ H = Ψ E . Although the LL approach has been successfully used for 1 m data on Peyto Glacier (Reference MunroMunro, 1989), Reference AndreasAndreas (2002) concludes that the HB approach works best for strong stability, which is more likely to be encountered above 1 m, where current AWS measurements take place. Both are used in resolving the utility of the bulk-transfer approach for glacier AWS data.
Assuming a fixed value for z0 (≈2.4mm), established from roughness-element description (Reference LettauLettau, 1969), the other lengths follow from the dynamics of the flow, using kinematic viscosity, v, in the roughness Reynolds number, Re* = u*z0/v (Reference AndreasAndreas, 1987):
Values for b 0, b 1 and b 2 specific to z H and z E are tabulated in Reference AndreasAndreas (2002) who, following re-analysis of datasets volunteered by others, finds further support for their use. Also, roughness-element description still appears to be an effective z 0 estimation procedure (Reference RaupachRaupach, 1992; Reference Smeets, Duynkerke and VugtsSmeets and others, 1999). These considerations, as well as a desire for as much consistency as possible with Reference MunroMunro (1989), are reasons to continue using them here.
3.3. Incorporating the OG parameterization
Following Reference Klok and OerlemansKlok and Oerlemans (2002), C H uz or C E uz in Equation (2) or (3) is modelled by a combined turbulent exchange parameter:

in which the terms to the right of Kb are K kat, where T a- Ts replaces ΔT in Equation (1). Kb is a background turbulent exchange parameter (also having the dimensions of a conductance), which represents the contribution of the geostrophic flow. It acts as an optimizing parameter, which may be adjusted to fit Q H and Q E to the surface energy balance, as was done by Klok and Oerlemans, or to independent sets of bulk-transfer estimates, as will be done here.
In formulating K kat, Reference Oerlemans and GrisogonoOerlemans and Grisogono (2002) set re« 0:0004, which scales katabatic temperature forcing of the glacier wind to Ta-Ts and, according to data from Pasterzenkees, causes sensible-heat-flux computations based upon K kat to agree with eddy correlation measurements when Pr≈5 is used in the parameterization. Although there is work to support Pr ___ 1 in strong stability (e.g. Reference Zilitinkevich and CalancaZilitinkevich and Calanca, 2000), Pr=1 is implied by the similarity framework for Equation (6), thereby causing an inconsistency between the bulk-transfer approach outlined here and the parameterization. Smaller Pr values, in the 1.1-1.5 range, have in fact been used by these investigators in their explorations of pure katabatic flows (Reference Grisogono and OerlemansGrisogono and Oerlemans, 2001, Reference Grisogono and Oerlemans2002), but it is beyond the scope of the work described below to find a definitive value for the Prantdl number in this context. Therefore the OG parameterization is examined as it stands, using Pr≈5.
Incorporating Equation (8), the turbulent heat-transfer expressions now take the form stated in Reference Klok and OerlemansKlok and Oerlemans (2002):


where K kat is determined by off-glacier AWS data, and K b by the need to fit the predictions of Equations (9) and (10) to bulk-transfer estimates made from Equations (2) and (3), using glacier AWS data. In this context, the bulk-transfer values are treated like a set of observations against which to compare the predictions.
One particularly notable point of difference between this study and the work of Reference Klok and OerlemansKlok and Oerlemans (2002) is that they use a variable ϒ in Equation (8) which is estimated from two off-glacier weather stations located at the extremes of the local elevation range, an approach which requires ϒ to be constrained to a lower limit of 0.0015 Km–1 to avoid extreme outcomes. Because there is only one such station for the Peyto Glacier basin, the OG parameterization is assessed mainly with the constraint of a fixed ϒ, which has the value of 0.005 Km–1 used in Equation (1) by Reference Oerlemans and GrisogonoOerlemans and Grisogono (2002). Nevertheless, this point does come up again for discussion in section 5.2 below.
3.4. Performance measures
Willmott’s index of agreement, d 2, between prediction, P, and observation, O, is used to assess model performance because it is more sensitive to bias than is the more commonly used r 2 (Reference WillmottWillmott, 1981; Reference WillmottWillmott and others, 1985):

where i refers to any of N observations that constitute the sample size. The limits of d 2 are 0 for complete disagreement, and 1 for complete agreement. Oi are obtained from the bulk-transfer expressions, using profile data at z = 1 m, or glacier AWS data taken at whatever height the sensors stand above the surface at the time of measurement. Pi are either bulk-transfer estimates from profile data at z other than 1m, or parameterized flux estimates made from off-glacier AWS data.
In addition to comparisons of mean values, measures of model performance also recommended by Reference WillmottWillmott (1981) include the root-mean-square error (rmse), and the systematic and unsystematic components of the rmse, respectively, rmseS and rmseU:



in which P’i = α + βOi , where α and β are from the least-squares regression of Pi upon Oi .
Significant bias is indicated when the rmseS is large in relation to the rmseU. In such cases, improvement may be expected as a result of optimizing the outcome of Pi .
4. Bulk-Transfer Results
4.1. Analysis
The objective of the analysis is to bring stability-corrected Q H estimates from different measurement levels above the surface into agreement with one another. This was done manually, by placing regression plots and the statistics as an interactive graphic within a spreadsheet, such that the effect of a change to Equation (4) upon the outcomes of Equation (2) could readily be observed. This was done as a series of trials for each of the micrometeorological datasets listed in Table 1, taking five iterations to complete each trial. At this stage of the analysis, the focus was upon d 2 and the extent to which stability correction would reduce Q H below Q H0, its simple logarithmic, or neutral, estimate at 1 m (Table 2). The 1 m level was chosen because it is common to all the datasets, and the use of the bulk-transfer approach at 1 m, using Equation (6a), seems to have compared well with eddy correlation in the past (Reference MunroMunro 1989). Thus Q H0 constitutes Oi in Equation (11); all other Q H values constitute Pi .
Table 2. QH/QH0 ratios, where QH0 is the neutral value at z = 1 m. Ratios listed are for no stability correction (Ψ = 0), log-linear correction (LL), Holstag and de Bruin correction (HB) and HB with no further correction beyond z/L = 1/3 (HB*). Boldface type identifies d2 ≥ 0.9
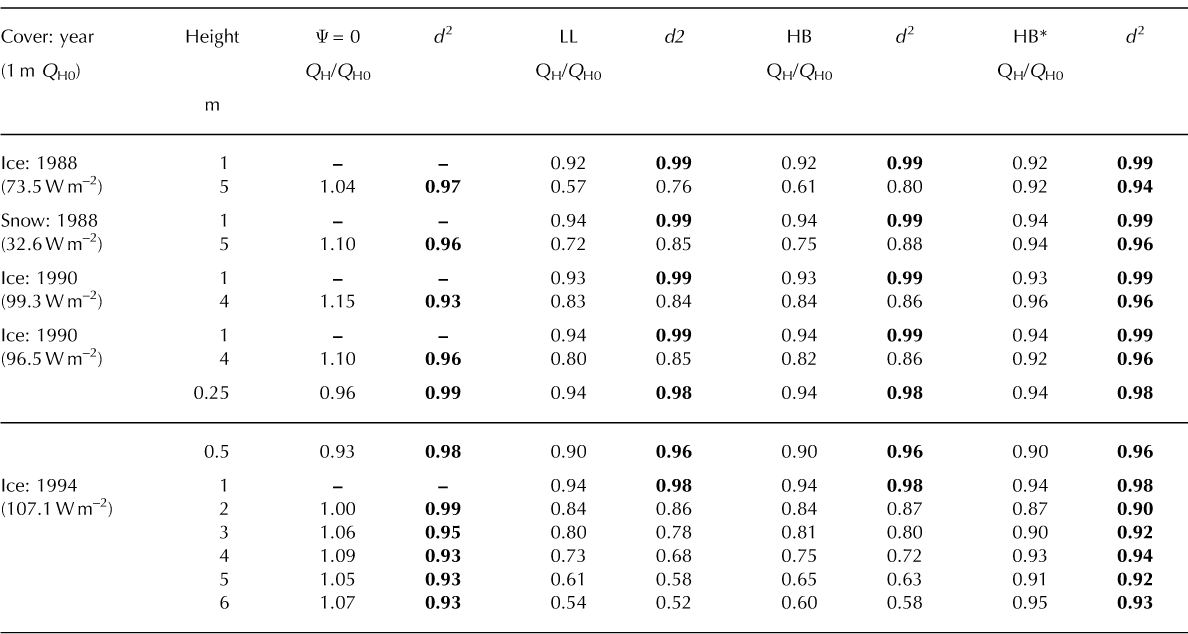
When no correction is made (Ψ = 0 in Table 2), d 2 ≥ 0.93 is found for all measurement levels. The Q H/Q H0 values above 2 m are remarkably consistent, deviating by no more than 0.04 from a mean value of 1.08, the exception being the first 1990 result. Small variability in Q H/Q H0 is consistent with the idea of a simple logarithmic regime in which ΨM, H, E can be represented by a constant, a possibility suggested by Reference Webb and MeteorolWebb (1970) regarding extension to strong stability. However, the observation that Q H/Q H0≥1 is indicated above 1 m in all cases, while Q H/Q H0<1 occurs below the 1 m level of the 1994 profile (Table 2), suggests that there is a z/ L-dependent stability correction to consider, though not necessarily one which depends much upon z/L above 1 m.
Before turning to the stability correction results, there is the caution that some of the outcomes may reflect measurement error. Taking the example of the 1994 profile for Ψ = 0, the 0.25 m result might be interpreted as anomalously high due to measurement error, though this could also arise from being too close to the roughness sub-layer (Reference Smeets, Duynkerke and VugtsSmeets and others, 1999). Measurement error might also cause the 0.5 and 2 m levels to be anomalously low, on the tenuous assumption that the 1 m measurements are correct in the first place. Be that as it may, the decision was made to proceed without data adjustment and see what would ensue from the stability corrections.
The effect of applying stability corrections for z≤1 m isto reduce Q H to no less than 0.90 Q H0, while maintaining d 2≥0.96, regardless of which approach is used (Table 2). For z > 1 m, Q H/Q H0 falls well below the 0.92-0.94 values obtained at 1 m, the ratio decreasing with increasing height above the surface for both the LL approach and the HB approach, the lowest occurring for LL. Although the 1 m Q H/Q H0 values appear to be somewhat high in relation to other work (Reference MunroMunro, 1989; Reference Van den BroekeVan den Broeke, 1997b), where ≈0.85Q H0 seems to be in order, values above 1 m tend to be well below 0.85. Marked reduction above 1 m is also found for d 2, its range being 0.52-0.86 for LL, and 0.58-0.88 for HB. Because the HB approach seems to be less susceptible to overcompensation than the LL approach, the idea of using a modified HB approach was explored.
The basis of the modification is to identify a maximum z/L value, a limit beyond which no further adjustment to Q H0 is made. To do so is to accept the idea of transition to a simple logarithmic regime when stability becomes sufficiently strong (e.g. Reference Webb and MeteorolWebb, 1970). It also revisits the notion of a critical stability number, a much discussed question to which there appears to be no definitive answer (Reference AndreasAndreas (2002)); nor is such an answer sought here, particularly in view of the likelihood that L is not suitable for stability scaling in a katabatic regime (Reference HolmgrenHolmgren, 1971; Reference Munro and DaviesMunro and Davies, 1978; Reference Grisogono and OerlemansGrisogono and Oerlemans, 2002). Rather, the z/L limit is explored in terms of an optimizing parameter that is adjusted to bring Q H estimates above 1 m into agreement with the 1 m values from each micrometeorological dataset, the caveat being that such a value would not necessarily apply elsewhere.
Again, this was done as an interactive spreadsheet exercise, proceeding by trial and error in search of a limit that best suited all the datasets listed in Table 2. Following many such trials, the decision was made to settle upon z/L≈1/3, the results of which yield the last two columns of Table 2. These show the closest correspondence between Q H/Q H0 at 1 m and its equivalents at other measurement levels, as well as d 2≥0.9 throughout, thus providing a reasonably consistent correction procedure.
4.2. Discussion
The results listed in Table 2 have been obtained iteratively, thus requiring multiple computations for each point in time to obtain a stability correction that has only a small, fairly consistent effect upon turbulent transfer estimates from one time-step to the next in the glacier ABL. Recognizing this, Reference OerlemansOerlemans (2000) adjusted the turbulent transfer approach such that C H, E in Equations (2) and (3) are represented by a single value which is adjusted to fit Q H and Q E to the surface energy balance over the period of interest. The implications of this and changes to other factors were investigated by a sensitivity analysis of the 1994 profile results.
For this analysis, all Q H above 1 m were listed in a single array of Pi a, and their corresponding 1 m estimates listed in a second array of Oi . Again, d 2 was obtained from Eqution (11), but the rmse values from Equation (12) were also included. Values of α and β for calculating Pi were obtained from regression, taking Pi to be the dependent variable (Fig. 4). The plot shown in Figure 4 is the end result of using a z/L = 1/3 limit to stability correction, where the statistics of the outcome constitute the first column in Table 3. Here, α and β are such that the averages, ō and P, work out to be nearly the same, while d 2 = 0.95 stands within the range of values listed in Table 2 now that they have been grouped together.

Fig. 4. Comparison of grouped QH estimates for z >1m with values at z = 1 m, including best-fit line. Crosses refer to QH values for z <1 m that are not used to fit the line.
Table 3. Sensitivity of bulk transfer to selected changes in calculation procedure, where z=L ≤ 1/3 or 1 is the limit beyond which no further stability correction is made, and boldface type identifies outcomes that include the three smallest rmseS
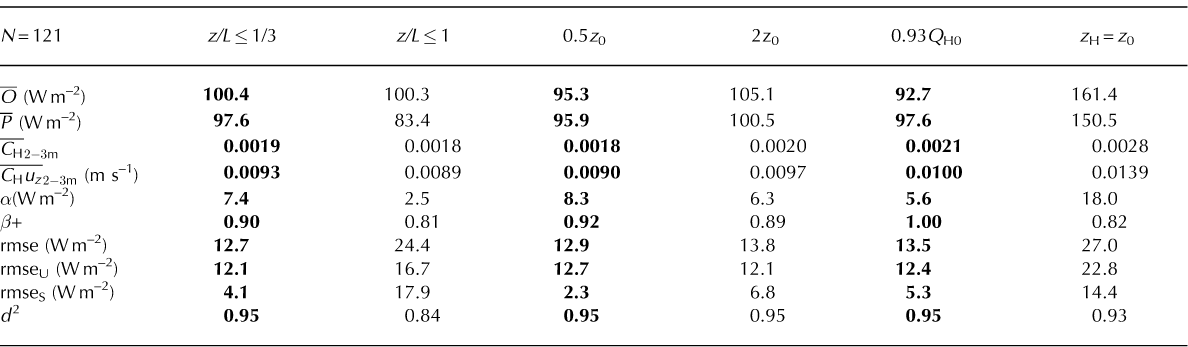
Also, the rmseU is approximately four times greater than the rmseS, which suggests that bias is not a major concern. Expressed in terms of the mean square error (MSE), the systematic portion accounts for approximately 10% of the total. In cases like this, where the rmseS is a relatively small contributor to the rmse, it is to be expected that d 2 may be greater than r 2 (Reference WillmottWillmott, 1981).
A perusal of Table 3 first shows the importance of the z/L limit where, following Reference Webb and MeteorolWebb (1970), a change to z/L = 1 produces markedly different ō and P, the lowest d 2 and the only case of rmseS> rmseU. Cutting z0 in half, or increasing each z by 0.125 m (half the distance from surface to lowest sensor) to invoke a zero displacement, has the effect of increasing z/z0 and improving some of the performance measures. Then ō and P are almost equal and the rmseS is minimal, its square accounting for approximately 3% of the MSE. Very much the opposite applies to doubling z0 or subtracting the zero displacement.
Attempts to simplify the calculations, by eliminating the calculation of stability corrections or setting z H = z0 to eliminate thermal roughness calculations, produce contrasting results. The elimination of stability calculations, by taking 0.93Q H0, produces results which are almost as good as those for z/L<1/3, where the rmseS and P—O are comparable to α, and β = 1 indicates the slope, at least, of a one-to-one relationship. Attempting to eliminate z H calculations, however, results in relatively poor performance, notably the largest rmse values and the next largest proportion of systematic to unsystematic error.
Hence, if simplification is required, it is better to eliminate stability calculations than to eliminate the calculation of a dynamic z H. Simplification is not the requirement here, so both features are retained in providing glacier AWS bulk-transfer estimates to compare with the OG parameterization.
A final comment with regard to Table 3 is to note that C H2-3m = 0:0019 (the first column in the table) is not very different from C H = 0:00127 used by Reference OerlemansOerlemans (2000) for Morteratschgletscher, despite the fact that the latter is a single value which was chosen to fit the energy balance to a 3 year sequence of melt data, separated by accumulation periods, such that one would expect seasonal changes in surface roughness. Also, it is to be expected that C H2-3m should vary among the cases shown in Table 3 because it depends upon the choices made with respect to roughness lengths and, through Re*, the treatment of stability.
5. Parameterization Results
5.1. Applying the off-glacier AWS datasets
The use of the AWS datasets required adjustment of base-camp temperature and humidity to the elevation of the ice station. This was done by applying a lapse rate of -0.0065°C m–1 to base-camp T a across the elevation difference between the two AWS sites, a correction of : ≈0.5°C, which more than compensates for the intercept in Figure 2b. For base-camp e a an atmospheric pressure ratio of ≈1.01 between the two sites is applied, increasing it by ≈6 Pa, which almost compensates for the intercept in Figure 2c. In view of the small elevation difference involved, nothing further was done by way of adjustment such as considering diurnal variation in the lapse rate.
The use of the glacier AWS required scaling the wind-speed measurements to the level of the temperature data. This was done by rearranging Equation (5b) to solve for uz , then applying u ≈2m/u ≈2m to the wind-speed data, a ratio which was within the range 0.9-0.95, where the lower end of the range applies early in the melt period, before thinning of the snowpack. The upper end applies to snow-free ice when the sensors are at their maximum height above the surface.
Again, an interactive spreadsheet approach was used, first taking five iterations to establish bulk-transfer Q H estimates in all years (Table 4), Q H + Q E in 2003 (Fig. 5), to serve as Oi in Equations (11) and (12). Then the corresponding heat transfers were estimated from off-glacier AWS data by way of the OG parameterization to establish Pi . Finally, Kb in Equation (8) was adjusted to force convergence between ō and P, the value of which is entered as O, P in Table 4.
Table 4. Performance measures, where Pi are QH parameterized from off-glacier AWS data, Oi are QH estimates from glacier AWS data, and optimization according to Kb forces ō = P. Italics identify the use of 0.93QH0 at z≈m for bulk-transfer estimates; bold italics show the results of using a diurnal γ variation model (~γ) in the OG parameterization
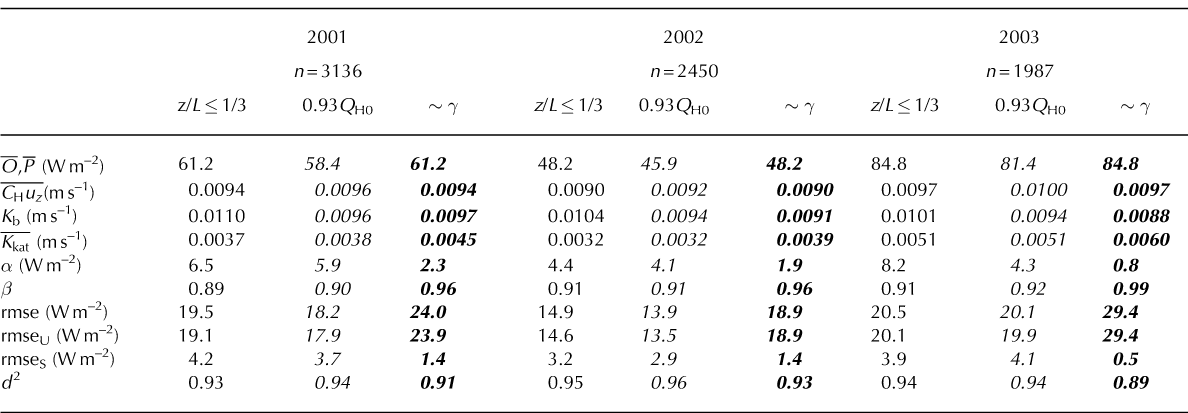

Fig. 5. Comparison of parameterized flux densities with bulk-transfer estimates for (a) sensible-heat flux density and (b) latent-heat flux density after optimizing according to QH + QE, and using a diurnal γ variation model.
5.2. Results and discussion
The results listed in Table 4 show high degrees of coherence between bulk and parameterized Q H in all three summers, where d 2 values are comparable to those listed in Tables 2 and 3. This is also true of 2003 if optimization according to Q H + Q E is done, the approach that would be taken if one were to optimize within the energy balance. The rmse values in Table 4 are larger than those in Table 3, almost exclusively with respect to rmseU, as may be expected when introducing new datasets. The rmseS values for z/L≤1/3 of each year differ little from the z/L≤1/3 result shown in Table 3.
Turning to the katabatic and background transfer coefficients, averages of the K
kat values (K
kat in Table 4) are slightly larger than that stated in Klok and Reference Klok and OerlemansKlok and Oerlemans (2002). As expected from Equation (1), the largest corresponds to the greatest ō, ![]() , and the smallest to the smallest ō,
, and the smallest to the smallest ō, ![]() . In contrast, the Kb
values used to obtain agreement between
. In contrast, the Kb
values used to obtain agreement between ![]() and ō are approximately three times larger than that which Klok and Oerlemans found suitable for their optimization. The different Kb values are more likely to reflect differences in time-frame and locale than to suggest deficiencies in approach. More to the point, the CHu
z entries in Table 4 consistently imply C
H
u
z
> (K
b + Kkat)=2, which is to be expected if Kb and K
kat represent flow well above the glacier surface.
and ō are approximately three times larger than that which Klok and Oerlemans found suitable for their optimization. The different Kb values are more likely to reflect differences in time-frame and locale than to suggest deficiencies in approach. More to the point, the CHu
z entries in Table 4 consistently imply C
H
u
z
> (K
b + Kkat)=2, which is to be expected if Kb and K
kat represent flow well above the glacier surface.
Out of curiosity, the comparison with Reference Klok and OerlemansKlok and Oerlemans (2002) was made again after multiplying K kat in Equation (9) by a factor of two, to mimic the effect of using Pr ≈ s 1 without changing re in Equation (8). This increases the influence of K kat, necessitating a smaller Kb, which has the effect of increasing rmseU by approximately 25% while causing little change in the rmseS. This suggests that to the extent that the errors in Table 4 are greater than those in Table 3, they are principally induced unsystematically by the parameterization because T a— Ts is used twice in the numerator of Equation (9) but only once in the numerator of Equation (2). The elimination of K kat from Equation (9) actually reduces the rmseU, but causes approximately a three-fold increase in the rmseS, because without the parameterization it is not possible to minimize bias by allowing temperature to regulate the strength of the heat exchange.
A matter of concern is how different the comparisons between bulk transfer and parameterization would be if changes were made to the bulk-transfer procedure, such as those listed in Table 3. The decision was made to focus upon the result of using 0.93Q H0, where Q H0 refers to neutral sensible-heat flux at zR¿2 m, because it is listed among the better performers in Table 3, it requires less calculation and it most closely replicates the approach taken by Reference OerlemansOerlemans (2000). Also, because it shows ¡3 = 1 in Table 3, this addresses curiosity about whether the same will occur in Table 4 where, despite good results for most performance measures, the regression parameters persistently deviate from a one-to-one relationship.
Using 0.93 Q
H0 caused little change in the performance measures, including a and j3. In contrast, one of the poor-performance options from Table 3, the removal of a dynamic z
H and z
E caused a slight decrease in d
2, a substantial rise in ō, ![]() and a need to increase Kb
by a factor of approximately 1.5 in order to achieve ō =
and a need to increase Kb
by a factor of approximately 1.5 in order to achieve ō = ![]() . More importantly, a and j3 for z
0 = z
H = z
E, deviate much more from a one-to-one relationship than any of the others and there are substantial increases in both components of the rmse, where the rmseS increases by a factor of at least two.
. More importantly, a and j3 for z
0 = z
H = z
E, deviate much more from a one-to-one relationship than any of the others and there are substantial increases in both components of the rmse, where the rmseS increases by a factor of at least two.
Hence, one could speculate about whether the incorporation of a dynamic z H E into the OG parameterization might result in a closer fit to the bulk-transfer values. However, it is perhaps better to speculate about the use of a dynamic 7 in Equation (8) for situations where only one off-glacier AWS is available. This was done by modelling the diurnal variation in 7 according to time, using a sinusoidal variation about 0.005 Km–1, such that the lower limit of 0.0015 Km–1 imposed by Reference Klok and OerlemansKlok and Oerlemans (2002) occurs between 1400 and 1500h, and an upper limit of 0.0085 Km–1 occurs 12 hours later. The consequences of doing this are interesting (Table 4): a substantially increased rmse and reduced d 2, but a major reduction in the systematic part of that error, and regression parameters which are virtually those of a one-to-one relationship.
At first sight, the results listed in Table 4 seem to present a dilemma: whether to adhere to a fixed γ, with its appeal of greater d 2 and a smaller rmse, orto use a variable γ in which systematic error has been reduced at the expense of smaller d 2 and a greater rmse. In fact, the latter is the only physically reasonable choice to make, one in which the cumulative importance of the rmseU fades over time and space, while that of the rmseS persists and grows. In all three summers, the systematic part of the error associated with Q H amounts to <1% of the MSE if the γ model is used.
Optimization according to Q H + Q E (Fig. 5) is dominated by the strength of the Q H component, so, if parameterizations of the two components are plotted individually against their bulk counterparts, that of Q H more closely approaches a one-to-one correspondence, albeit with increasing scatter for large Q H (Fig. 5a). For Q E, where j3 = 0:88 (Fig. 5b), it is well to note that the influence of Q E is small, the absolute range of its values being approximately one-fifth that of Q H. Also, removal of the 1.07 multiplier from the glacier AWS relative humidity data increases j3 in Figure 5b only to R¿0.94.
Because the optimization results displayed in Figure 5 apply to total turbulent heat transfer, rather than to each component individually, there are differences between ō and ![]() for both Q
H and Q
E, but they are well within 1 Wm–2. So, if the bulk-transfer estimates presented here are taken to be a standard of some kind, this bodes well for extended application of the OG parameterization.
for both Q
H and Q
E, but they are well within 1 Wm–2. So, if the bulk-transfer estimates presented here are taken to be a standard of some kind, this bodes well for extended application of the OG parameterization.
Concluding Remarks
The foregoing analysis outlines an approach to estimating heat fluxes from glacier AWS data, where instruments tend to be mounted sufficiently far above the surface to cast doubt upon the use of bulk-transfer procedures. Even so, it appears that by applying a restricted form of stability correction to bulk-transfer formulae, plausible heat-flux estimates can be obtained. The nature of the restriction signifies not so much an extension to strong stability as it does yet another recognition that the glacier ABL is different from that of the flat, non-glacierized surface and that limiting the use of stability correction is the best that can be done in such a context.
Noting the absence of a calibration standard, it is readily acknowledged that plausible bulk heat-flux estimates are not necessarily correct estimates. In addition to expressing concerns about the application of bulk-transfer theory in katabatic flow, one could criticize measurement quality. The instrumentation used in this study does not meet the highest standards of precision and comparability. On the other hand, it does represent the standard that many investigators who use robust instruments for AWS sites have at their disposal.
Also, to those who are familiar with the use of electrical analogues in evaporation modelling (e.g. Reference Monteith and UnsworthMonteith and Unsworth, 1990), K b and K kat in Equations (9) and (10) would seem to be like the branches of a parallel
conductance circuit in which Kb is a tuneable conductance. Thus, in addition to being able to tune in the effect of the geostrophic wind, it is also possible to tune out the effects of incorrect assumptions about the value of the Prandtl number, or about off-glacier air-temperature data being free of the glacier cooling effect. It follows that parameterization can yield plausible heat-flux values despite concerns about theory and physical setting.
Nevertheless, it is gratifying to see correspondence between glacier AWS estimates of the heat-flux densities and those which are parameterized from the off-glacier AWS because it independently confirms that data from the glacier surroundings are useful for modelling turbulent heat transfer to glaciers in a way which lends itself to mapping (e.g. Reference Klok and OerlemansKlok and Oerlemans, 2002). Furthermore, the inclusion of a simple γ variation model extends the range of what can be done with a single off-glacier AWS, though not to the extent of ignoring the option of using more than one station if more are available. Whatever doubts one may have about data quality and theory, there is a strong indication here that the OG parameterization, optimized with background turbulence, constitutes an effective approach to the extensive modelling of turbulent heat exchange over melting glaciers.
Acknowledgements
Support for this work has been provided by various agencies over the years: the University of Toronto, the Natural Sciences and Engineering Research Council of Canada and the MSC’s Cryospheric System (CRYSYS) to assess global change. The research is done within the context of the National Glacier Programme of the GSC, which provides field infrastructure support and research collaboration. A special note of appreciation is extended to other researchers and students who have worked with me in the field, most notably T. Bain, P. Cutler and G. Grant, and to the reviewers, E. Andreas and B. Grisogono, whose comments resulted in important revisions to the manuscript.











