Introduction
Ice streams are fast-moving glaciers within the grounded portion of the West Antarctic ice sheet. Some tens of kilometers wide and several hundreds of kilometers long, the ice streams are the principal drainage routes for the inland reservoir of ice. Changes in ice-stream flow, such as the recent stoppage of Ice Stream C, alter the storage of ice and affect global sea level. The basic mechanism of ice-stream motion has not been understood. A necessary step in achieving such understanding is to identify the sites of resistance to flow.
The flow of all glaciers is driven by gravity, as described by the driving stress. On most fast glaciers, large velocities are attained because the driving stress is large. For example, Byrd Glacier, an outlet glacier from East Antarctica, travels at about 800 m a−1and has a driving stress of 250 kPa (Whilans and others, 1989). The grounded portion of Jakobshavns Isbrae in Greenland travels at about 3 km a−1under a driving stress of a few hundred kPa (Reference Echelmeyer and HarrisonEchelmeyer and Harrison, 1990; Reference Echelmeyer, Clarke and HarrisonEchelmeyer and others, 1991). Such fast flow due to large gravitational forces is understandable in terms of conventional glaciological theory. However, Ice Stream B reaches Speeds of as much as 82 m a−1, yet its driving stress is only about 15 kPa (Reference Alley and WhillansAlley and Whillans, 1991), less than 10% of the value for other fast glaciers. Ice Streams D and E have somewhat larger driving stresses and similar fast speeds (Reference Bindschadler and ScambosBindschadler and Scambos, 1991; Reference MacAyeal, Bindschadler and ScambosMacAyeal and others, 1995). This lack of obvious linkage between speed and driving stress has been a major enigma when addressing questions of the ice sheet and its stability.
Glacier flow is controlled by a balance between driving stress and stresses opposing the flow. The small driving stresses on the West Antarctic ice streams indicate that net resistance to flow must be equally small. This resistance may originate at the glacier bed (basal drag), at the lateral margins (lateral drag) or from gradients in longitudinal stress (Reference Van der Veen and WhillansVan der Veen and Whillans, 1989). Measured surface Velocities have been used to show that longitudinal stress gradients are unimportant to the large-scale balance of forces on Ice Stream B (Reference Whillans and van der VeenWhillans and Van der Veen, 1993a). Thus, resistance on this ice stream must be some combination of drag from the bed and lateral margins.
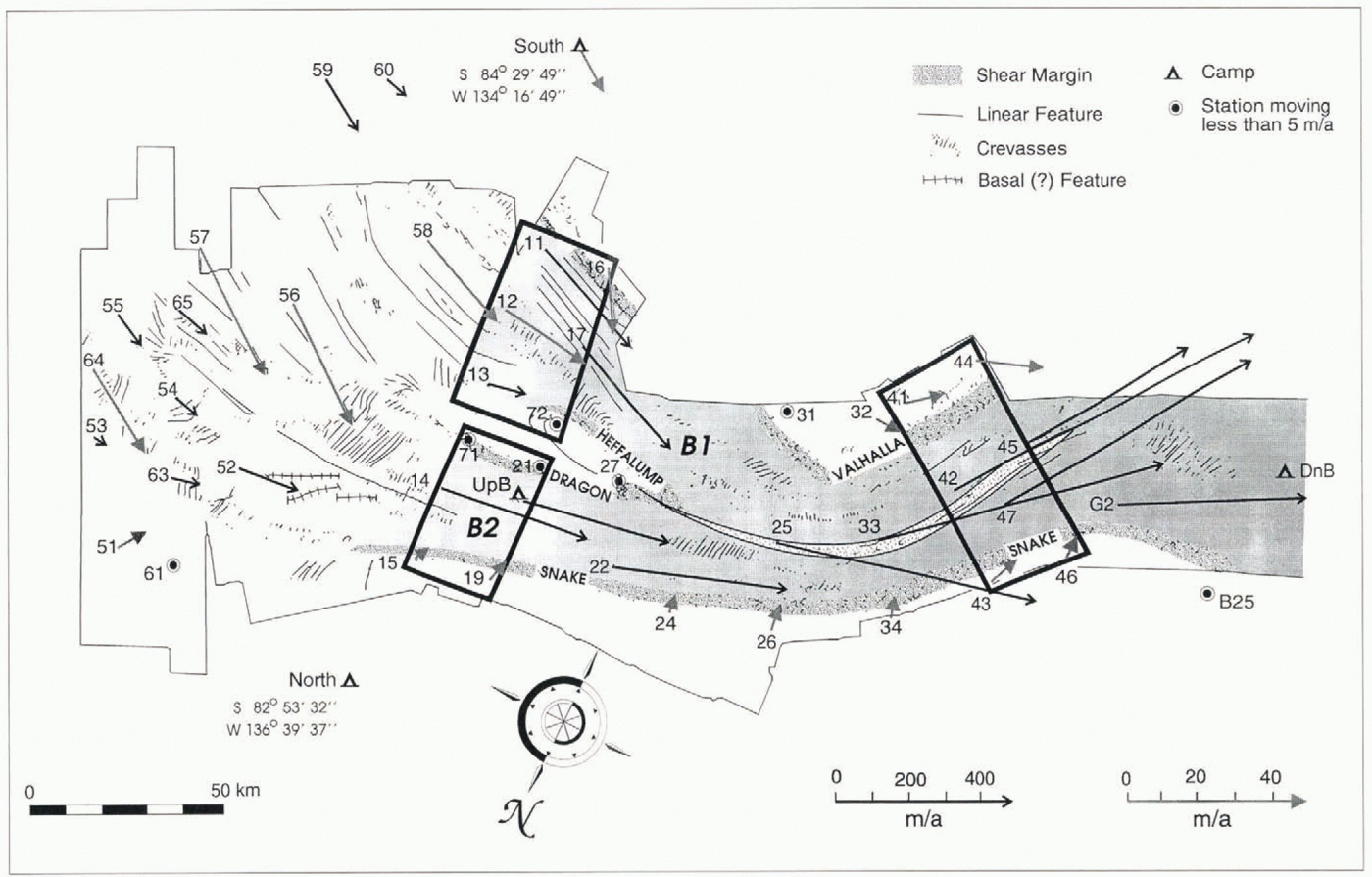
The present study addresses the issue of the relative importance of lateral and basal drags for Ice Stream B. The basic data set used derives from repeat aerial photogrammetry, providing numerous determinations of surface speed and surface elevation. For each of three selected regions (shown in Figure 1), many transects of velocity are available, allowing the role of lateral drag to be evaluated more fully than in prior studies.

Fig. 1. Location map showing the main surface features of Ice Stream B, based on aerial photogrammetry. Numbers refer to ground-based stations where velocities (represented by the arrows; note the two different scales) were measured using Transit satellite tracking (Reference Whillans and van der VeenWhillans and Van der Veen, 1993a). Shading represents the active ice stream. The three areas studied in this contribution are indicated by the boxes, and cover tributaries Bl and B2 and the narrow region downstream of the confluence of these tributaries.
Prior studies have addressed the role of lateral drag as well. For Ice Stream B, Reference Bindschadler, Stephenson, MacAyeal and ShabtaieBindschadler and others (1987)and Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994)use single transects of velocity near the DNB and UpВ camps, respectively. For Ice Stream E, Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995)applied inverse control methods to infer basal drag. The limitation in that work is that it has been difficult to obtain sufficiently accurate values of the regional surface slope, as needed to calculate the driving stress, and there may be important limits on the spatial resolution of velocity determination in shear zones.
The present study has the advantage of good spatial coverage of velocity determination and precise and accurate surface slope determinations.
Estimating Lateral Drag
Theory
Resistance to flow from lateral drag can be estimated by considering how the lateral shear stress, R xy,. varies across the ice stream. The xaxis is chosen in the direction of flow and the yaxis perpendicular to it; the components of velocity in these directions are represented by Uand V,respectively. The shear stress is linked to the shear strain rate, or transverse gradient in ice velocity, using the inverse formulation of Glen’s flow law for glacier ice, with exponent n= 3
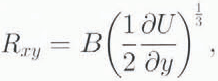
in which Brepresents the temperature-dependent rate factor (Reference HookeHooke, 1981).
In adopting this equation, a number of simplifying approximations are introduced, The first approximations is that ![]() is the dominant strain rate, so that the effective strain rate may be replaced by the shearing rate. Reference Whillans, Chen, van der Veen and HughesWhillans and others (1993)show that longitudinal tension and lateral compression are of secondary importance in the region near the UpB camp, so that these strain rates can be neglected. Inspection of the surface velocities in the other areas considered in this study indicates that this result may be extended to all photo blocks. The second approximation made here is that flowline turning, as described by the along-flow gradient in the transverse component of ice velocity, ∂V/∂x, is negligibly small. Thus, the shear strain rate is mainly determined by the transverse gradient in the along-flow velocity, ∂U/∂yNone of these approximations is critical. A further approximation is that the shear strain rate may be considered constant with depth. The large speeds on Ice Stream B suggest that most of the flow is associated with basal sliding and so the shear strain rate varies little with depth. Thus the resistive force from the sides can be estimated from observed surface speeds.
is the dominant strain rate, so that the effective strain rate may be replaced by the shearing rate. Reference Whillans, Chen, van der Veen and HughesWhillans and others (1993)show that longitudinal tension and lateral compression are of secondary importance in the region near the UpB camp, so that these strain rates can be neglected. Inspection of the surface velocities in the other areas considered in this study indicates that this result may be extended to all photo blocks. The second approximation made here is that flowline turning, as described by the along-flow gradient in the transverse component of ice velocity, ∂V/∂x, is negligibly small. Thus, the shear strain rate is mainly determined by the transverse gradient in the along-flow velocity, ∂U/∂yNone of these approximations is critical. A further approximation is that the shear strain rate may be considered constant with depth. The large speeds on Ice Stream B suggest that most of the flow is associated with basal sliding and so the shear strain rate varies little with depth. Thus the resistive force from the sides can be estimated from observed surface speeds.
Two equivalent methods for estimating full-thickness forces were considered. One approach is to use a rate factor, B,in the flow law Equation (1)) appropriate for near-surface temperatures, and the depth of strong ice, which is less than the full ice thickness. The other approach is to use a depth-averaged and temperature-weighted rate factor together with the full thickness of the glacier. The second approach is simpler, and is used here. Thus, the lateral force equals HR xyper unit length in the ice-stream direction, in which Hrepresents full thickness, and a temperature-weighted rate factor is used in Equation (1).
The net resistance from lateral drag per unit width of ice stream is (e.g. Reference Van der Veen and WhillansVan der Veen and Whillans, 1989)

The ice thickness, H, is nearly constant across the ice stream (Reference Retzlaff and BentleyRetzlaff and others, 1993). Taking Hindependent of yand substituting Equation (1) for the shear stress gives

Applying this expression to measured transects of velocity, U(y),allows the role of lateral drag to be assessed across the width of the ice stream.
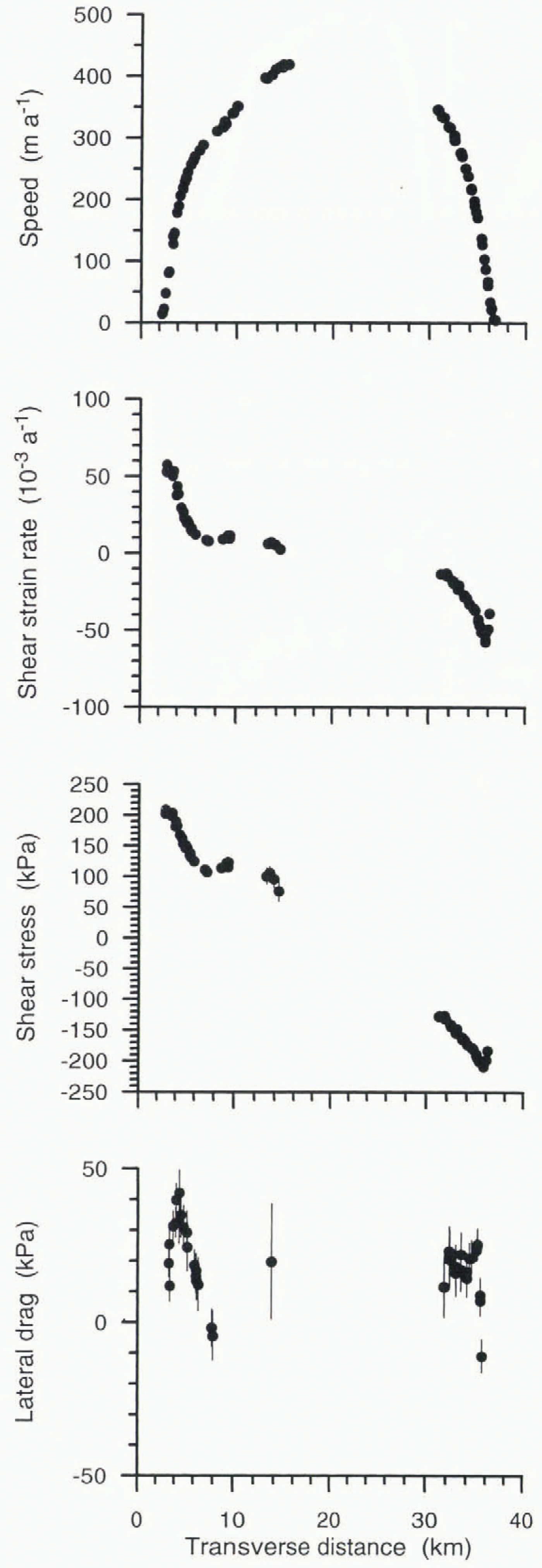
The steps involved in the calculation are shown in Figure 2for a single transect. The upper panel shows one transect of the along-flow component of velocity, U, derived from repeat aerial photogrammetry. The lack of data for the interval 16 < y< 31 km is due to the absence of visible surface features in the central part of the ice stream. From these velocities, the shear strain rate (second panel) is estimated. Applying the flow law Equation (1)), the shear stress (third panel) can be evaluated. The transverse variation in shear stress is a measure for resistance to flow associated with lateral drag (lower panel). In this calculation, a constant rate factor is used (В= 540 k Pa a−1/3). This value is the temperature-weighted rate factor, based on the temperature profile measured in a borehole to the bed near the UpB camp (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990) and values of Bgives in Reference HookeHooke (1981).

Fig. 2. Steps in estimation of lateral drag from measurement of velocity along a single transect. The Upper panel shows the ice speed, U, and the second panel the shear strain rate or half transverse gradient, ![]() The third panel shows the shear stress, R xy,calculated from the shear strain rate using a rate factor B = 540 K pa a−1/3from Reference HookeHooke (1981), and temperature-weighted according to the temperature profile measured in a borehole to the bed near the UpB camp (Engelhardt and others. 1990)). The lower panel shows lateral drag, calculated from F lat= (∂/∂y)(HRxy). This particular transect covers tributary B2, about halfway between station 14 and the UpB camp. Ice flow is towards the reader.
The third panel shows the shear stress, R xy,calculated from the shear strain rate using a rate factor B = 540 K pa a−1/3from Reference HookeHooke (1981), and temperature-weighted according to the temperature profile measured in a borehole to the bed near the UpB camp (Engelhardt and others. 1990)). The lower panel shows lateral drag, calculated from F lat= (∂/∂y)(HRxy). This particular transect covers tributary B2, about halfway between station 14 and the UpB camp. Ice flow is towards the reader.
Error propagation
The calculated resistance from lateral drag is proportional to the second derivative of ice speed as shown by Equation (3). Consequently, small measurement errors may translate into large uncertainties in the results. The uncertainty in velocity determination, σ u, is about 4 m a−1(Reference Whillans, Chen, van der Veen and HughesWhillans and Others, 1993). The propagated error in shear strain rate, ![]() , in which Δyrepresents the distance over which the transverse velocity gradient is calculated. To avoid unacceptably large errors, and yet still describe local patterns, velocity determinations at least 1 km apart but no more than 2 km apart are used. This leads to a maximum error in strain rale,
, in which Δyrepresents the distance over which the transverse velocity gradient is calculated. To avoid unacceptably large errors, and yet still describe local patterns, velocity determinations at least 1 km apart but no more than 2 km apart are used. This leads to a maximum error in strain rale, ![]() Shear strain rates reach values that are an order of magnitude larger than this error estimate (Fig. 2). The associated error in shear stress can be estimated from
Shear strain rates reach values that are an order of magnitude larger than this error estimate (Fig. 2). The associated error in shear stress can be estimated from

In the shear margins, R xyreaches about 200 k Pa (third panel), while the shear strain rate is on the order of 0.05 a−1. Thus, the error in the shear stress at the margins is about 4 k Pa. Applying this error in Equation (2), the uncertainty in resistance from lateral drag, ![]() is about 3 k Pa for transverse gradients calculated over distances larger than 1 km (the ice thickness is about 1000 m). The error may be considerably larger towards the center of the ice stream where small values of ∂U/∂ytend to magnify the effect of measurement uncertainties. Consequently the error bars in the lower panel of Figure 2are larger near the ice-stream center.
is about 3 k Pa for transverse gradients calculated over distances larger than 1 km (the ice thickness is about 1000 m). The error may be considerably larger towards the center of the ice stream where small values of ∂U/∂ytend to magnify the effect of measurement uncertainties. Consequently the error bars in the lower panel of Figure 2are larger near the ice-stream center.
Local fluctuations
There are local fluctuations in ice velocity on the ice stream. Such variations have been observed on the strain grid deployed near the UpB camp (Reference Whillans and van der VeenWhillans and Van der Veen, 1993b; Reference Hulbe and WhillansHulbe and Whillans, 1994) and are also evident in the velocities obtained from repeat aerial photogrammetry (Reference Whillans, Chen, van der Veen and HughesWhillans and others, 1993). Initially, it was believed that these fluctuations might be associated with flow over and around basal features. However, the patterns in velocity and surface slope do not correlate as would be expected due to a basal disturbance. Moreover, the surface topography migrates with time (Reference Hulbe and WhillansHulbe and Whillans, 1994).
The anomalous local patterns in velocity may be due to horizontal contrasts in ice strength. Deformation is concentrated in what seem to be narrow (about 500 m wide) bands of soft ice embedded in the main body of the ice stream. However, the weighted-mean rate factor across the ice stream, allowing for soft bands, is only a little smaller than the value used here. The effect of local variations in the rate factor is taken to be like noise that can be mitigated by averaging.
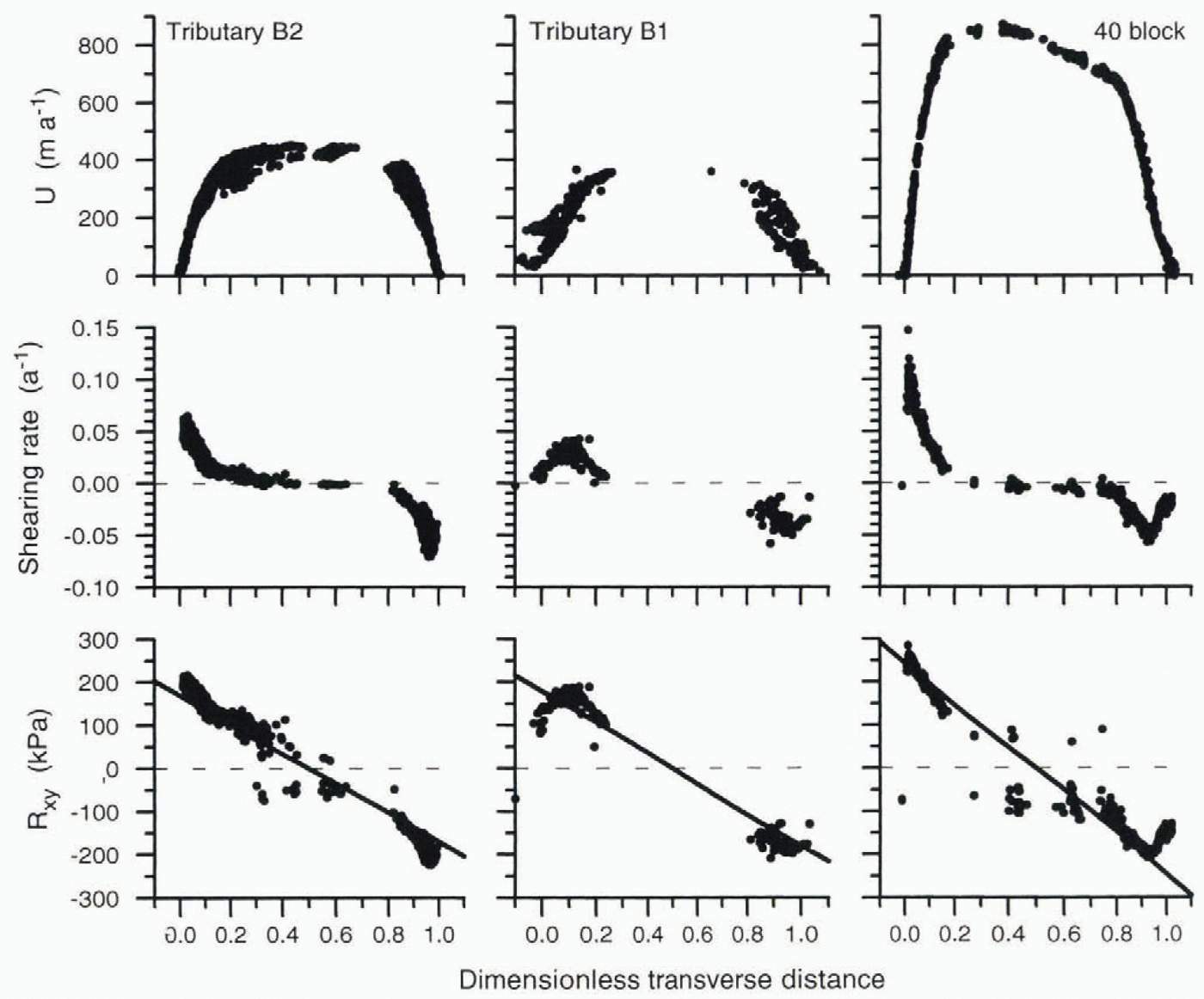
This local noise is removed by accumulating many transects of velocity. Instead of considering single transects, as in Figure 2, multiple transects obtained from repeat aerial photogrammetry are used. This results in the graphs shown in the upper panel of Figure 3. To further reduce the effect of local fluctuations, the calculations are also conducted using the transverse gradient in shear stress evaluated over only the central part of the ice stream in the discussion of force budget. This reduces the effect of measurement error and effectively averages over local fluctuations.

Fig. 3. Profiles of measured ice speed and derived quantities across the ice stream for the three photo blocks shown in Figure 1. Direction of flow is towards the viewer. The shear stresses in the lower panels are calculated using Equation (1) with rate factor = 540 kPa a−1/3. The solid line represents the theoretical gradient if the sides oppose all of the action of the ice stream.
Data
Photogrammetry
Velocities and surface elevations used in this study derive from repeat aerial photogrammetry conducted in January 1985 and January 1986. The positions of surface features (mainly crevasses) recognizable on both sets of photographs are measured to obtain displacements and thus velocities (Reference Whillans, Chen, van der Veen and HughesWhillans and others, 1993). Scale and orientation for the linked aerial photographs are provided by photo targets set up at some of the surface stations where velocities were measured using Transit satellite tracking (Reference Whillans and van der VeenWhillans and Van der Veen, 1993a). The arrows in Figure 1represent velocities at the ground stations. The locations of the three photo blocks used in this study are shown in Figure 1; the “10 block” covers the two tributaries Bl and B2, and the “40 block” the narrow portion of the combined ice stream.
Photogrammetric velocity determinations are restricted to those parts of the ice stream where surface crevasses are present, which is primarily the region of the shear margins and inward. Near the center, there are fewer, if any, crevasses, resulting in data gaps. For tributary B2, additional velocity determinations along the Strain grid near the UpB camp (deployed in a region free from exposed surface crevasses) are available and used in this study. These measurements are represented by the cluster of points centered around s= 0.6 (sbeing the transverse coordinate) in the upper left panel of Figure 3.
Transects of velocity
A single accumulated transect of velocity is prepared for each of the three photo blocks by stacking separate narrow transects. Velocity determinations within each 1 km wide transverse band are used to calculate the shear stress, R xy.These values are added according to a dimensionless transverse coordinate. This is necessary because, in general, the opposing sides of the ice stream are not mutually parallel. For example, over the length of the B2 photo block (27 km), the width of the ice stream decreases by about 15%. The dimensionless coordinate is defined as the distance from the southern margin, divided by the ice-stream width. The width is lhe distance between sites of zero along-flow component of velocity. These sites are determined by visually extrapolating the measured speeds near both margins. The speed approaches zero asymptotically, and so the width is not precisely determined. However, a more sophisticated procedure to determine the local width would not significantly alter the results presented here. The accumulated transects are presented in Figure 3.
This procedure introduces an error in accumulated shear stress because of uneertainty in separating transverse velocity gradients from the along-flow gradient in speed. For the photo block covering tributary B2, the along-flow stretching rate is typically about 5 × 10−3a−1(Reference Whillans, Jackson and TsengWhillans and others, 1993), and the speed may change by as much as 5 m a−1over the width of each band. This constitutes a velocity error for each 1 km wide band and, by itself, leads to an error in lateral shearing rate of as much as 0.03 a−1, which is additional to the measurement errors discussed earlier. The net uncertainty in a single determination of shear stress is then about 40 kPa in the lateral margins. For the entire photo block, there are 27 transects, so the error in shear stress reduces to about 8 kPa.
An alternative procedure, that would eliminate both the error introduced by collecting all velocity determinations in each band into a single transect, and the need for using a dimensionless transverse coordinate, is to interpolate the irregularly spaced data to regular grid nodes. This was done by Reference Whillans, Jackson and TsengWhillans and others (1993)for the B2 photo block. However, the tested gridding routines perform rather poorly near the lateral shear margins where sharp changes in the along-flow component of speed occur. Reference Whillans, Jackson and TsengWhillans and others (1993)tried to alleviate this problem by adding synthetic data just outboard of the shear margins, thereby forcing the gridded values to become zero in the shear margins. However, this procedure affects the gridded results even in the shear margins which, for the present study, are potentially the most important parts of the ice stream. Therefore, attempts at gridding the data were abandoned and the actual, irregularly spaced velocity determinations are used.
Results
Shear stress
Shear stress is calculated from the transects of measured ice speed. For each of the three photo blocks, the results of the major Steps involved in this calculation are shown in Figure 3. The upper panels of Figure 3display the measured speeds, and the middle panels show the calculated shear strain rate, or half the transverse gradient in ice speed. Uncertainty in the rate factor, B,due to experimental limitations (Reference HookeHooke, 1981) allows for values as much as 25% different in the lower panels. For this calculation, the middle value for the rate factor as recommended by Reference HookeHooke (1981)is used, and no allowance is made for softening of the ice in the margins.
Comparison with driving stress
To assess whether lateral drag is important in controlling ihe motion of the ice stream, the gradient in shear stress is compared to the driving stress. The driving stress is calculated using the familiar formula involving surface slope and ice thickness,

where hrepresents the elevation of the ice surface, and ρthe density of ice. The surface slope is the average over the full length and width of each photo block. If lateral drag provides all resistance to flow, force balance requires
or, using Equation (2)and (5)and taking the ice thickness, H,constant,

This theoretical gradient is indicated by the solid lines in the lower panels of Figure 3. It is the physically most extreme gradient in shear stress that could occur. A larger transverse gradient in R xyWould indicate lateral resistance to flow exceeding the driving stress, which would be possible only under unusual circumstances.
The values of the driving stress derive from elevations and thicknesses given in Reference Retzlaff and BentleyRetzlaff and others (1993).The elevations are ultimately tied to good-quality surveys by Transit Statellite tracking and have a standard error of 4–9 m. The estimated standard error in thickness is 30–60 m. These values lead to a calculation uncertainty of less than 1 k Pa in driving stress.
The points in the lower panels of Figure 3approximately follow the solid line based on this driving stress. Scatter is greatest near the center line, where calculation uncertainties are largest. Nearer the margins, points tend to be more different from zero than the solid line, perhaps due to ice softening. At the extreme left and right limits, the calculations show a trend of values decreasing toward zero. This is an effect of increased basal drag at the outboard edges of the ice stream. Neglecting values from the margins, the pattern of calculated values of R xywithin the ice stream accords with the solid line. This agreement indicates that lateral drag is sufficient to oppose most or all of the driving stress. Or, stated differently, resistance to flow associated with lateral drag balances most of the driving stress. By implication, basal drag must be near zero.
Most of the scatter apparent in Figure 3can be attributed to local fluctuations in ice speed. Variations in R xyare largest near the center of the ice stream where the shear strain rate approaches zero. Because of the non-linearity of the flow law, small fluctuations in Velocity and shearing rate lead to larger fluctuations in calculated shear stress here.
Softening of the margins
Near some of the lateral margins, the calculated points in the lower panels of Figure 3tend to be more different from zero than the solid, theoretical line. That is, the points tend to curl away from this line. The most straightforward interpretation is that the ice may be softer at those sites than supposed in the calculation. Strain heating associated with intense lateral shear raises the temperature of the marginal ice, making this ice softer. In addition, the Strength of the ice in the margins may be altered if a pronounced fabric develops. For example, if the сaxes are aligned perpendicular to the shear margin, the ice would be about 40% softer than isotropic ice (Reference Van der Veen and WhillansVan der Veen and Whillans, 1994). An alternative and basically equivalent interpretation is that a smaller effective thickness should be used in the margins, because deep ice is warmer and hence weaker than near the ice-stream Center line and less of the thickness supports large stresses. Softening or reduced effective thickness could be incorporated in the calculations by using a smaller rate factor where appropriate. This would reduce the calculated values of the shear stress, R xy, and bring the points in Figure 3closer to the solid line. To eliminate the extreme calculated values of Rxy,a 20% softening or effective thickness reduction in the shear margins would be sufficient.
An independent estimate of the softening in the margin is not available. The amount of softening of the marginal ice relative to the ice in the center of the ice stream depends on the temperature of the ice before entering the shear margins, on possible changes in fabric, and perhaps other factors. Much of this uncertainty may be avoided by omitting marginal ice from the calculation of force budget, and considering only the central part of the ice stream. It is done both ways in the next subsection.
Large-scale force budget
Another way to discuss the results shown in Figure 3is to consider the balance of forces acting not on an infinitesimally narrow slice of ice stream as in the lower panel of Figure 2, but on the full, or nearly full, width. This is done by integrating Equation (2)over the width, 2W. This gives the mean resistance from lateral drag acting on the ice stream,

where y = ±Wrepresents the positions of the lateral margins. If the shear margins are to be omitted, W represents a smaller distance from the dynamic center line. The shear stress is approximately equal (but of opposite sign) at both margins (Fig. 3). Denoting the value of |Rxy| at the outer limits of the calculation by Ts, Equation (8)becomes

It may be noted that this expression for the net lateral drag acting on the ice stream does not involve any assumption about the transverse variation in shear stress.
The width-averaged force-balance equation can be written as

in which gradients in longitudinal stress are neglected because they are unimportant if spatial averages are considered (Reference Whillans and van der VeenWhillans and Van der Veen, 1993a; on the local scale longitudinal stresses may be important, as shown by Reference Whillans and van der VeenWhillans and Van der Veen (1993b)). The overbar denotes the areally averaged value for the photo block. Results for the three photo blocks are given in Table 1.
Table 1. Force-budget tems for the three photo blocks on Ice Stream B. The two values Used for the factor in the non-linier flow law for glacier ice correspond to the average value of 540 kPa a -1/3, and to the lower limit of 400 kPa a1/3applicable to the temperature profile measured near UpB using the temperature dependence of the rate factor as given in Reference HookeHooke (1981). Compared to the uncertainty in rate jactol; other sources cif error are negligibly small. The center portion of each photo block is defined as the central 60% ojthe ice stream, extendingfrom s = 0.2 to s = 0.8, wilh s the dimensionless transverse coordinate
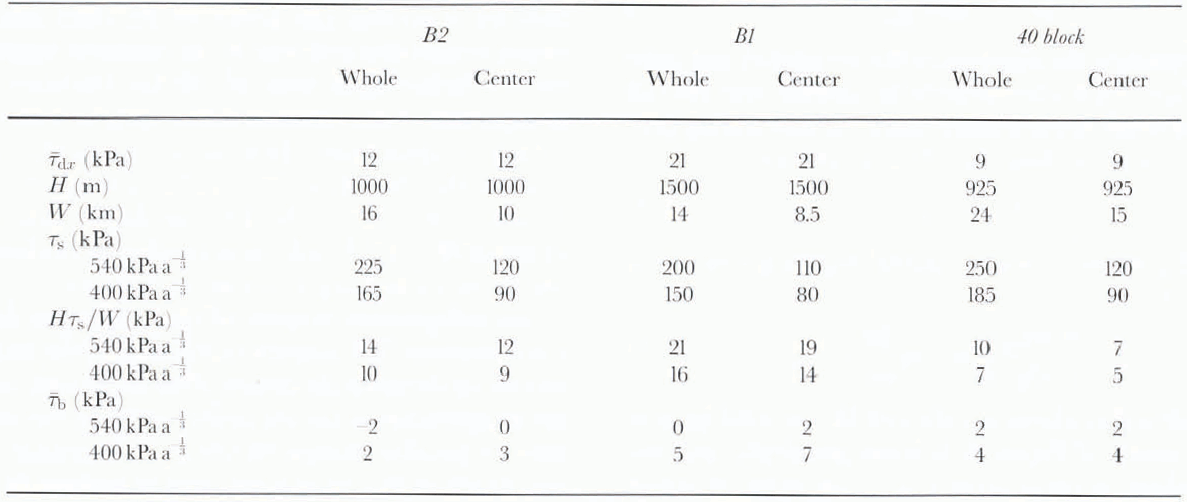
According to these calculations, lateral drag supports most or all of the driving stress in all three areas studied. For the region near the UpB camp (tributary B2) and the 40 block farther down-glacier, inferred basal drag is only a few kPa, with an upper limit of about 4 kPa. For tributary B1, the upper estimate of basal drag is about twice this value (7 kPa).
Comparison with Other Studies
The region near the DNB camp, in the vicinity of the grounding zone where Ice Stream B enters the Ross Ice Shelf, has been studied by Reference Bindschadler, Stephenson, MacAyeal and ShabtaieBindschadler and others (1987). The very small driving stress (2.58 ± 0.20 kPa) is balanced primarily by resistance from lateral drag (2.14 ± 0.46 kPa), with a negligible contribution from basal drag (0.44 ± 0.46kPa). Gradients in longitudinal stress are unimportant in this region. These results are similar to those obtained here.
Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994)measured a transect of velocity from the center of the ice stream near the UpB camp, southward through the shear margin and on to the slow-moving interstream ridge. Following basically the same procedure as in Figure 2, the shear stress at the margins is calculated to be 170 kPa (similar to values obtained here). This value suggests that the margins provide most or all of the resistive force on the whole section of the ice stream considered (3.7 × 108N per meter of ice-stream length in the flow direction, compared to a total gravitational driving force of 4.0 × 108N). However, further analysis and modelling of the velocity profile along the transect leads Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994)to conclude that resistance to flow must be partitioned equally between lateral and basal drags. This second, contradictory, interpretation arises from an assumption that local fluctuations in ice velocity are due to large-scale forces and not local strength and driving-stress variations (as done here).
Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994)also conducted numerical modelling. In a first attempt, the theoretical velocity profile obtained by assuming zero basal drag and constant ice stiffness agrees poorly with the measured profile. To improve agreement, Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994)apply Equation (3)to calculate lateral drag along the transect. Ignoring lateral fluctuations in driving stress, they find that calculated values of basal drag are negative. To eliminate these untenable results, large transverse variations in the rate factor are needed. However, short-distance fluctuations in the driving stress can reach more than six times the areal average and should be included when attempting to model local velocity variations along a transect.
Another study that addresses the partitioning of flow resistance on West Antarctic ice streams is that of Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995)for Ice Stream E. That study indicates that resistance from lateral drag, and perhaps gradients in longitudinal stress, are important in the overall budget of forces, with large areas of the ice streams experiencing almost zero basal drag. It is concluded that the area-averaged basal drag supports about 29% of the driving stress of Ice Stream E. This is comparable to the upper estimates of basal drag given in Table 1. Most of the calculated basal resistance on Ice Stream E is concentrated in small-scale sticky spots. There is no evidence for sticky spots on Ice Stream B (Reference Whillans and van der VeenWhillans and Van der Veen, 1993a, Reference Whillans and van der Veenb; Reference Whillans, Jackson and TsengWhillans and others, 1993), but, as noted by Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995), the areas on Ice Stream B considered in these studies are comparable in size to some of the sticky-spot-free zones on Ice Stream E. Furthermore, on most of Ice Stream E, the driving stress is about 50 kPa, which is about four times the areally averaged driving stress on Ice Stream B. This indicates a major difference between the two ice streams, Ice Stream E being Steeper and thicker, and so various resistances to motion must be larger.
Conclusions
Lateral drag is the primary control on the flow of Ice Stream B, with almost zero contribution from basal drag. This finding agrees with results from seismic studies conducted in the vicinity of the UpB camp suggesting that, at least locally, the bed under Ice Stream B consists of a weak, water-saturated layer of till (Reference Blankenship, Bentley, Rooney and AlleyBlankenship and Others, 1986). It also agrees with strength tests performed on samples retrieved from the bed in the same vicinity that indicate a very small yield strength, about 2 kPa (Reference KambKamb, 1991). The present work shows that these properties are not restricted to the vicinity of the UpB camp, but apply to large parts of the ice stream. The ice stream must be mainly underlain by a soft, weak layer of ponded water or weak debris.
The major limitations to any study addressing lhe budget of forces are uncertainties associated with the value of the rate factor, B,and, perhaps, the form of the constitutive relation. In this study, as well as in those referred to above, the ice is taken to deform according to Glen’s flow law. More important is the appropriate value to be used for the rate factor in this flow law. According to Reference HookeHooke (1981), the uncertainty in Bmay be as large as 25%. However, even in the extreme, with the lower limit of the rate factor used, and the potentially soft margins excluded, lateral drag provides 55% (40 block) to 75% (tributary B2) of the flow resistance.
The model for ice-stream mechanics that follows from this study is very simple, but rather different from models advanced earlier. Prior models emphasized friction emanating from the bed and discussed the importance of viscous dissipation in mobile drift, the thickness of the subglacial water layer, and the role of drainage conduits. While these processes are very important to the question of Weakening of the bed, once the ice stream has started, basal processes do not seem io control the speed of the ice stream. Instead, control is from the sides where rather large (up to about 200 k Pa) shear stresses operate.
Acknowledgements
We thank R. Bindschadler and an anonymous referee for comments. This research was supported by the U.S. National Science Foundation (grant No. OPP-9316509). This is Byrd Polar Research Center contribution No. 1031.