Velocities, strain rates, stresses, crevassing and faulting on Glacier de Saint-Sorlin, French Alps, 1957–76

Abstract

Stake surveys on Glacier de Saint-Sorlin, French Alps, during the period 1957–76 show that annual surface velocities fit a linear vectorial model, with a term depending on the site, another on the year, and an important random component. Strain rates, viscosities and stresses at shallow depth are computed using strain triangles of hectometric (10² m) size. Between 1961/62 and 1972/73 the isotropic point, where streamlines cease to converge, moved downstream about 200 m. This trend may explain increasing velocities. Crevasses appear where annual strain is > 1.2%. Faults limit the effective shear stress at the surface to about 0.38 bar. Ten modes of flow are distinguished, instead of only two for the two-dimensional model (compressive and extensive). The gradients of shallow stresses, which ensure extra driving forces, are computed with another mosaic of triangles of similar size (stress triangles). There are also important extra driving forces at the bottom, which force the flow to deviate from the direction of the steepest surface slope. Two criteria allow elimination of stress triangles where these unknown basal extra driving forces are important. Even so, no sliding law in terms of mean annual values can be obtained. This study shows that the classical perturbation theory, which explains advances and retreats by the arrival of kinematic waves, is unsuitable for glaciers of kilometric size.

1. Introduction

From the equation of mass conservation, which has been linearized by considering small perturbations from a reference state, a deterministic relation may be derived between mass balance on a glacier and advances or retreats of its terminus (Weertman, 1958; Nye, 1960, 1963; Lliboutry, 1965, p.739–762). This equation, known as the “equation of kinematic waves”, has been used without having been checked directly. And, when it was tested, the test was negative. Among glaciers that do not obey the classical equation are Nisqually Glacier, Washington, U.S.A. (Meier, 1968), and the French Alpine glaciers Glacier d’Argentière above its icefall (Hantz, 1981), Mer de Glace below its icefall (Lliboutry and Reynaud, 1981) and Glacier de Saint-Sorlin (Vincent and others, 2000). This failure of the usual mathematical model has three origins:

1. 1. A fixed relation has often been assumed to exist between the basal shear stress and sliding velocity. In fact, at least one additional independent variable intervenes: the water pressure at the interface.

2. 2. The velocities along a vertical profile are assumed to depend only on the local thickness, surface slope and bed slope, but actually they also depend on deviatoric stresses that may be transmitted over kilometres.

3. 3. To consider annual advances or retreats as mere perturbations of a reference state is incorrect, since these perturbations are the main terms in the equations. The geometry of the ice edge, and the body and external forces applied to it, determine the flow. In addition, the balance at the surface controls the yearly advance or retreat, and gradually modifies the surface profile on a decadal time-scale. Therefore, in general, a thickening of the glacier tongue is not synchronous with its advance, nor is thinning synchronous with retreat. The change in thickness leads the response of the terminus position.

The goal of this paper is to clarify these points by analyzing field data obtained on a real glacier, rather than by considering glacier models, which are always more or less unrealistic. This study will allow assessment of published analyses and better planning of future glacier monitoring. A geographical description of Glacier de Saint-Sorlin and its old terminal moraines is given in a companion paper (Lliboutry, 2002). In the present paper, the subglacial topography of Glacier de Saint-Sorlin is described, and fluctuations of surface velocities from year to year are analyzed. The existence of a seemingly random component, already recognized in some much larger glaciers (Meier, 1971, 1974), is stressed. Strain rates and stresses at shallow depth in 1972/ 73 are computed and related to the many faults observed at the surface. The driving forces in the upper layers of the ablation area are calculated. (This leads to the choice of a sound way of computing first and second derivatives of a function of x and y, which is known at some points only.) It is found that these shallow driving forces cannot explain why the flow deviates from the direction of the steepest surface slope. Moreover, in some places, even taking these shallow driving forces into account, the horizontal shear obtained is excessive, leading to negative sliding velocities. Thus, at depth there are extra strain rates and driving forces that cannot be estimated from surface data and knowledge of the thickness alone, and any attempt to deduce an empirical law for annual sliding velocities will be unsuccessful. Finally, the changes in surface strain rates and shallow driving forces from one year to another are computed, since they may throw light on this essential point, but this can be done with confidence only in a restricted area.

2. Methods

2.1. Topography

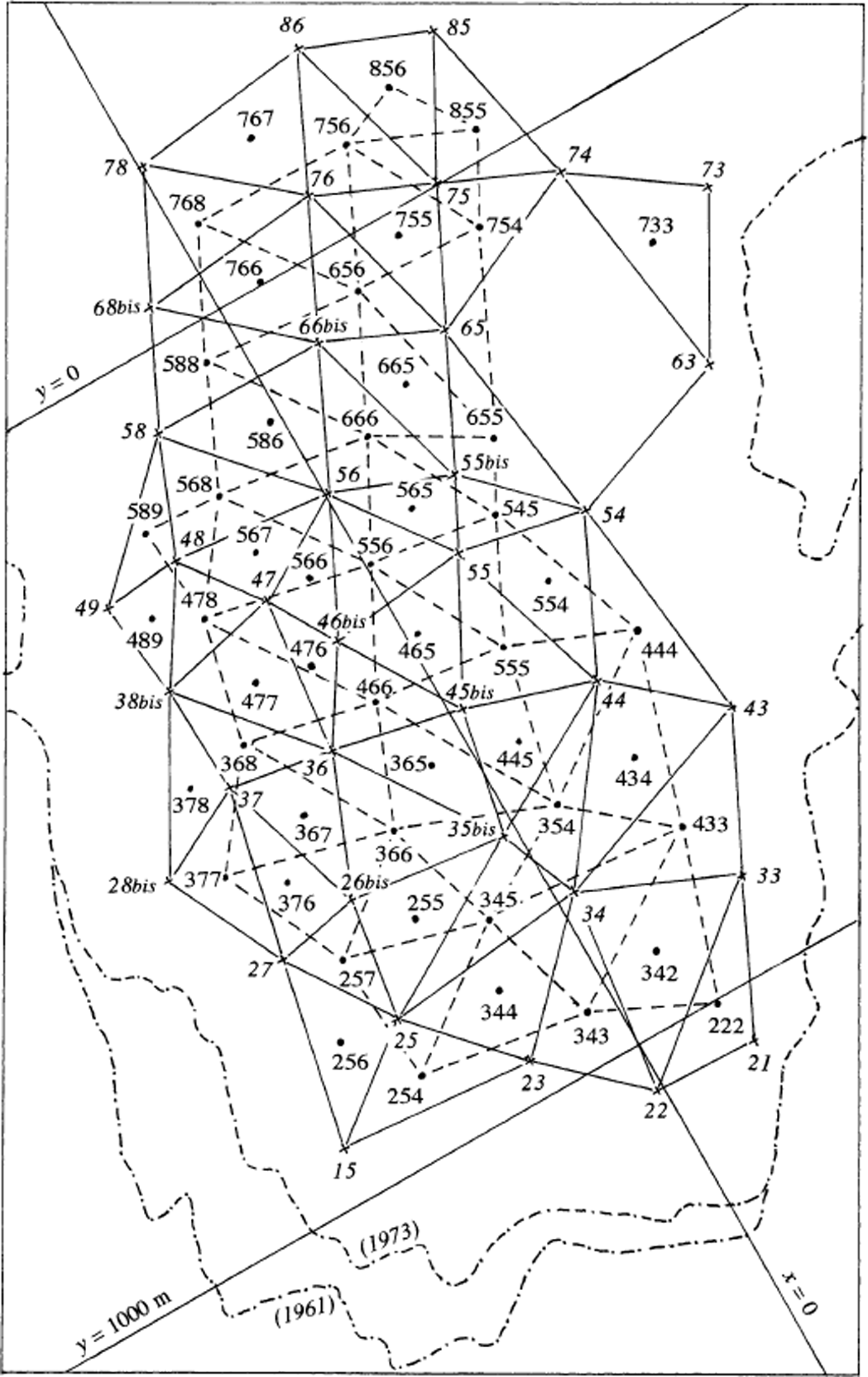
The local geodesic net, which is determined with an accuracy of 1 cm, is shown in Figure 1. It has been linked to four points of the French geodesic net, allowing determination of (X, Y) coordinates in the French National system (Lambert coordinates). The Lambert projection does not modify angles. In the area studied, the Y axis of Lambert coordinates has a bearing of 2.664° with respect to true north (see Lliboutry, 2002, fig. 1). Bearings with respect to this direction (the Lambert north) will be called the azimuths. Modified Lambert coordinates (x = X −901 000 m and y = Y −325 000 m) are used in all maps in this paper.

Fig. 1. Local geodetic net, and sightings used for its determination. Triangles indicate the points used for plotting aerial photographs.

Stake coordinates in successive years, and all data derived from them that were used herein, are filed at Laboratoire de Glaciologie et Géophysique de l’Environnement, Grenoble, France, and will be sent on request (contact C. Vincent). The locations of stakes are shown in Figure 2. In the stake numbers, the first digit is the transverse row, starting from the terminus, and the second digit identifies, approximately, a streamline, increasing from west to east. Because annual displacements were small compared to the average distance between neighbouring stakes (about 130 m), they are not taken into account when variations in velocity are discussed. Each stake defines a permanent fixed “site” on the glacier. When a new stake was not set exactly on the flowline of an old one that had melted out, the new stake is labelled “bis”.

From 1959 to 1972, ablation stakes were surveyed, to 1 cm, by sighting their tops from the three points A–C. Later, a faster method was used: sighting from points close to each stake to metallic poles placed around the glacier. The altitude of the tops of the stakes was determined by measuring vertical angles. The accuracy of vertical positions is an order of magnitude less than that of horizontal positions (some decimetres instead of some centimetres) because of abnormal and variable atmospheric refraction on glaciers. (For this reason the vertical velocity of stakes is not used in the present study.) A standard correction for the elevation of a point at a distance D, which accounts for the Earth’s curvature and atmospheric refraction, is qD ², with q = 6.8 × 10⁻⁸ m⁻¹. Precise geodesic levelling in 1972 showed that correct values in August (with either overcast or clear sky) ranged from q = 0 to q = 10⁻⁸ m⁻¹ for sights that were half over moraine and half over ice. q was actually negative when the sight was over snow (for sight to Etendard, q = −13.7 × 10^–8 m^–1).

Fig. 2. Surface velocities at stakes in 1972/73. Surface as on 16 August 1971, with 10 m contour interval. The map is oriented with the highest elevations (south-southwest) at the top and the terminus (north-northeast) at the bottom. The grey streak is a faint medial moraine.

2.2. Geophysical exploration

The only published thicknesses of Glacier de Saint-Sorlin, drawn from a seismic survey (Belin, 1962), contain mistakes. Good seismic surveys of the ablation zone and gravimetric studies of the whole glacier were undertaken in 1975 and 1976. Glacier thicknesses thus found, and others based on borings between 1968 and 1977, are published here for the first time.

2.3. Borings

In 1967 and 1968, core drilling using an auger driven by the Minuteman rotary machine of Crælius reached the bed at 36 and 60 m, respectively. In 1968 a 6 kW electrical corer, with an uninsulated heating element, obtained uncracked cores, 2 m long, at a rate of 6 m h⁻¹. These cores were used to determine the liquid-water and salt content of the ice (Dupuy, 1970). Subsequently, Gillet (1975) used a hot-water drill and attained rates of up to 60 m h^–1 during the first hour. This system was used exclusively in 1972 (17 holes bored, 1063 m in total). However, this device cannot be used in firn, where water is lost. A light electrical borer with a silver head, 20 mm in diameter, was then perfected and used in 1974 and 1977.

In August 1970, four pressure gauges were inserted at the bottoms of boreholes and sealed in place with a plug of refrigerated ice.

3. Data

3.1. Glacier thickness

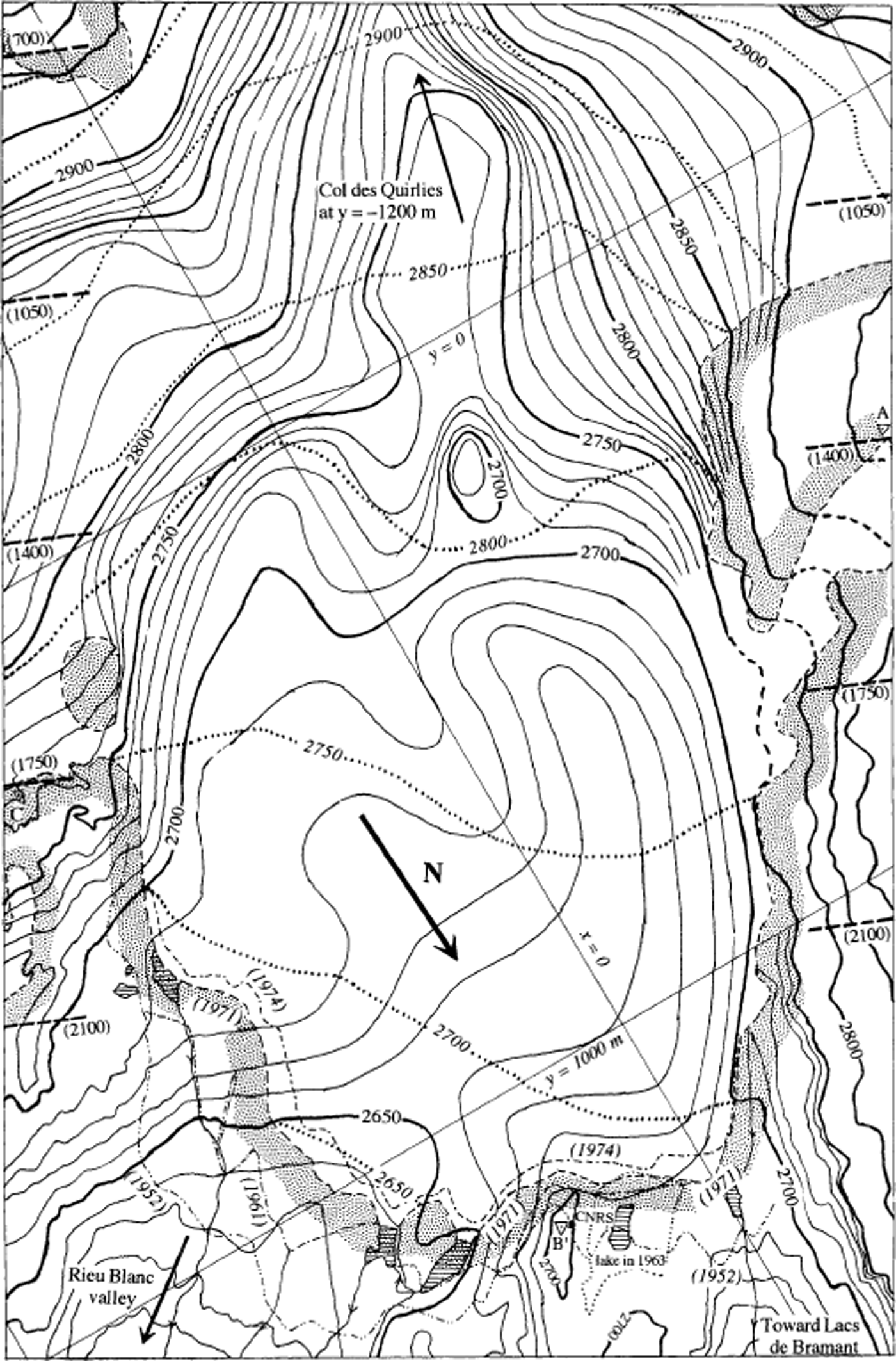
The three classical ways of measuring ice thickness — seismic exploration, gravimetry and drilling — are complementary. Seismic exploration may lead to serious mistakes when it is not checked by gravimetry; gravimetry is accurate only if drilling to the bed allows calibration; and thermal borings may be misleading if the drill tip encounters a steeply sloping bed and slips along the bed. (At the foot of Etendard, in 1974, it was believed that bottom had not been reached after all available cable, 204 m, was uncoiled. Seismic exploration the following year showed that the ice thickness there was only 140 m.) As all three methods were used in constructing the present map of the bed (Fig. 3) and cross-sections, one every 350 m (Fig. 4), we can trust these results. The standard error at any point should be ±5 m.

Fig. 3. Bed topography and terminus positions in 1952, 1961, 1971, 1974.The map is oriented as in Figure 2. Contour interval: 10 m up to 2900 m. Contour interval on the glacier surface in August 1971: 50 m. Locations of cross-sections in Figure 4 are indicated.

Fig. 4. Cross-sections of Glacier de Saint-Sorlin every 350 m, starting from Col des Quirlies, all with azimuth 111.5°. Glacier surface is from August 1971. No vertical exaggeration.

Glacier de Saint-Sorlin differs significantly from the infinite plane slabs or the glaciers in straight cylindrical valleys that many theorists use in their simulations, notwithstanding that it is quite typical of mountain glaciers of its size. Thicknesses are commonly about 30 m on the steep western part, and 60–70 m in the central area with low surface slopes. However, there is a subglacial valley running from Col des Quirlies towards Lacs de Bramant (north-northeast) where ice thicknesses are 100–140 m. This valley appears to lie along the projection of some visible beds of soft Liassic (early Jurassic) and Triassic rocks. Glacier erosion has produced two overdeepenings in this valley: the upstream one has a closure of ∼25 m, and the downstream one, just southwest of the Centre National de la Recherche Scientifique (CNRS) hut (Fig. 3), was about 40 m deep. The latter, however, has been breached by a broad opening towards the Rieu Blanc valley (northeast). Thus, the axis of the subglacial valley turns ∼60° to the right, 300 m up-glacier from the CNRS hut. As we shall see, it is this hidden subglacial north-south “rail” which deflects the ice flow from the northeast direction of the surface slope.

3.2. Annual and seasonal surface velocities

In the area studied, components of the surface velocities in the x and y directions, denoted u and v, respectively, are positive and of the same order. Annual velocities in 1972/73 at 37 stakes are shown in Figure 2 (arrows). They converge in the upper part of the ablation area (rows 8 and 7), and diverge slightly downstream (rows 5–2). When annual velocities at the same site in different years are compared, a significant source of discrepancy may arise from the fact that stake surveys could not always be done at the same time of year, after the end of the melt season. In 1965 the survey was done on 28 July, in 1968 on 12 August, and in 1969 on 19 August. Thus the interval 1965/66 includes August twice, and the interval 1967/68 only includes one-third of August. Thus, the increase in surface velocities, due to seasonally larger sliding velocities, may be underrepresented in some years and overrepresented in others. Such increases in sliding speed should be most common at the end of June and during July, at the climax of the melting season, but may also continue into August.

Unfortunately, to correct for this inconsistency in survey dates, the only data at our disposal are extra surveys of stakes 45 and 66 done on 19 June 1957 and 3 August 1958. Assuming that seasonal fluctuations were perfectly periodic during these years, one may infer mean velocities for 19 June–3 August (early summer), 3 August–7 September (late summer) and 7 September–19 June (“winter” velocities). These are given in Table 1.

Table 1. Magnitude and azimuth of mean seasonal velocities

In early summer, velocities at both stakes increased significantly, and the azimuth shifted counterclockwise. At stake 45, 420 m downstream from stake 66, this increase was a little larger than at stake 66, but it decreased faster. Probably the summer increase of ice flow is important only in the central ice stream. In June 1972 an extra survey yielded an apparent uplift of the central area of the ablation zone of up to 1 m, but this uplift was no longer present in August (personal communication from C. Carle, 1972). The June data were thought to be erroneous and were not kept. Since this phenomenon has been observed elsewhere (Hodge, 1974; Iken and others, 1983) and has been attributed to water storage at the bed, it may not have been an error.

3.3. Subglacial water pressures

Water levels in boreholes that reached the bed near the terminus become steady in September (Table 2). Borehole 1967 was halfway between stakes 15 and 23, borehole 1970-1 was near stake 23, borehole 1970-2 was near stake 25, and borehole 1970-3 was near stake 27. The moderate values of N, the effective pressure (ice lithostatic pressure, on the hectometric scale, minus local water pressure), are conducive to separation on the lee faces of the microrelief. The altitudes reached by water in the boreholes (Table 2) are consistent with a phreatic surface sloping gently towards the terminus. Thus, the cavities should be interconnected. Because borings into bedrock with a diamond bit encountered about 1 m of loose debris near the terminus (and none upstream), the interconnection may well be through the debris layer.

Table 2. Steady water levels in boreholes in September

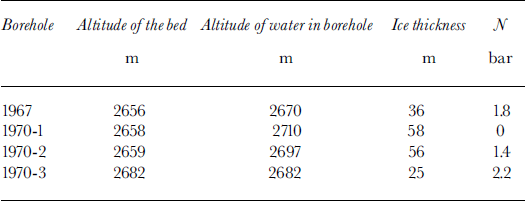
An interesting case is borehole 1970-1, where the glacier is more or less afloat and the bottom drag is thus low, maybe negligible. Just 200 m downstream from this point, the glacier ended as an ice cliff between 1957 and 1963. Before the formation of a lake, the base of this cliff was accessible. The basal ice had very large crystals, with randomly oriented c axes. All entrapped air was gathered into elongated, finger-sized, vertical bubbles. During the century or so required to cover this 200 m distance, this ice had obviously suffered post-kinematic recrystallization without being subjected to important deviatoric stresses, a fact that suggests almost zero friction.

4. Analysis of Annual Surface Velocities

4.1. Fluctuations, 1965–74

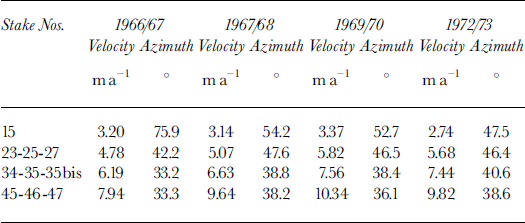
Displacements between two annual surveys yield annual velocities. These velocities are weighted means of often quite different seasonal values, but, as with most glaciers that have been studied, they are the only values at our disposal. The mean velocities for the three central stakes of each of rows 2–4, which move at similar rates each year, are presented in Table 3. Data are given for the year when velocities were lowest, 1966/67, for 1967/68, for the year when they were highest, 1969/70, and for 1972/73 when there were more stakes, permitting more detailed study. Most of the differences between years undoubtedly come from the strong increase in sliding velocity in summer, which is not the same in all years. However, when the annual velocity increased, it rotated counterclockwise only at stake 15; elsewhere it rotated clockwise. Because accelerations differ from year to year, changes in the driving forces should be similarly variable.

Table 3. Magnitude and azimuth of annual velocities

For the 8 years 1965–73 we have velocities at up to 20 sites, from stake 15 to stake 55. This gives, for each velocity component, a table of data with 8 columns and 20 lines. Of the 160 cells in this table, we have values in 125. As suggested by Hantz (1981) for Glacier d’Argentière, it is worth adopting a linear statistical model to analyze these data. At site j, in year t, u and v have the values:

(1)

Parameters and are the averages over the 8 years at a given site. Parameters Δu _t and Δv _t are the same for all 20 sites in a given year t, and their mean is zero. r_jt and are centred random variables, called residuals. Assuming that they have a Gaussian distribution and that they are independent of each other, the best linear unbiased estimators (BLUEs) for the 56 parameters of the model are easily computed.

A simplified method for doing this, without matrix calculus, is given by Lliboutry (1974) for the case of mass balances rather than velocities. Let h_jt be an occupancy function, equal to 1 when there are data in the (j, t) compartment and to zero otherwise. First approximations of are:

(2)

These approximations allow one to calculate first centred approximations for the Δu _t:

(3)

Successive approximations and are then calculated in turn, completing the 20 × 8 table prior to each iteration using the last computed virtual values and . Three successive approximations were enough to obtain exact decimals to the third place. Finally, the residuals for the 125 measured values are calculated.

Δu _t and Δv _t are negative in 1965/66, despite the inclusion of two Augusts in this time interval. In addition, Δv _t is positive in 1967/68, which includes only one-third of August. This seems to prove that during this entire period, 1965–73, sliding velocities were not enhanced in August and thus the comparison of annual velocities is sound. No systematic changes of sign of the residuals appear, as would occur if a kinematic wave were noticeable at this spatial scale. All residuals for u and v are plotted in Figure 5. There is no obvious correlation between them. Fifty percent of the points lie within a circle of radius 0.3 m a⁻¹. Sixteen per cent are found outside a circle of radius 0.6 m a⁻¹, a ratio that does not falsify the assumption of a Gaussian distribution. The largest residuals are for stakes 15, 22 and 28, which are closest to the receding terminus, and for stakes 44, 45 and 47, which have large increases in summer velocity. Given the low velocities, the random term may be important. The mean values of Δu _t and Δv _t are plotted in Figure 6, which may be called the odograph of the mean velocity vector for the entire area studied. The annual changes are of the same order as the random “noise” above.

Fig. 5. Residuals of the linear model. Half of the points are within the circle with radius r = 0.3 m a⁻¹ (median value). The six stakes that yield residuals larger than twice the median are named (numbered).

Fig. 6. Mean annual velocity at 20 stakes in 1965–73. The mean velocity is a vector going from the origin to successive peaks of the zigzag line. Inset above shows this line (odograph) magnified five times.

4.2. Surface strain rates and stresses: equations

To compute surface strain rates and stresses, the coordinate axes are tilted so that the surface becomes the xy-plane. Because the surface slope is < 0.17 at distances > 200 m from the terminus, neither x and y, nor u and v need to be modified. From general theory, the strain rates are:

(4)

When the frame of reference is rotated by φ about the z axis, the new strain rates are:

(5)

The rotation does not modify defined by:

(6)

Since τ_xz = τ_yz = 0 at the surface, the z axis is a principal direction for the stresses. Assuming isotropic rheology, it is also a principal direction for the strain rates. As ice is incompressible and no firn is found in the area, the corresponding principal strain rate is:

(7)

The other two principal strain rates are and , with and not necessarily between them. Let A ₁ = −φ ₁ and 90° −φ ₁ be the azimuths of the corresponding principal directions in the xy-plane. (Azimuths are positive in the clockwise direction, whereas φ is positive in the anticlockwise direction.) Using:

(8)

Equations (5) yield:

(9)

Considering the signs of the strain rates, it is found that:

(10)

Surface strain rates are drawn from annual displacements, and thus the values obtained are annual means. Because most of the seasonal fluctuations come from sliding, seasonal fluctuations of surface strain rates should be much smaller than velocity fluctuations. Therefore, it makes sense to calculate deviatoric stresses from annual strains. An isotropic third power law of viscosity is assumed. Let τ_ij denote deviatoric stresses, and τ and represent the effective shear stress and twice the effective shear strain rate, respectively, thus:

(11)

With σ_x, σ_y and σ_z denoting the normal stresses (with atmospheric pressure omitted) and noting that σ_z = 0 at the surface, the last of Equations (11) reads:

(12)

It follows that:

(13)

Since σ_z = 0 at the surface, the mean normal stress is:

(14)

The principal stresses (which have the same directions as the principal strain rates) are σ ₂ = 0 and:

(15)

The value of at the surface, say , is obtained from:

(16)

Laboratory experiments have shown that B increases with the water content of temperate ice. Its recommended value is B = 0.44 bar⁻³ a⁻¹ (Lliboutry, 1987, p. 123, 451) corresponding to a liquid water content of 0.65%. In the area of Glacier de Saint-Sorlin under consideration, the water content was found to be about zero near the surface, 1.04% at 25 m depth, and 1.24% at 55.5 m depth (Dupuy, 1970). Thus 0.65% may well be a reasonable mean value for the upper 30 m. In any case, owing to the exponent 1/3, the stresses inferred from the given strain rates are not very sensitive to the value of B.

Let tan α_x and tan α_y be the slopes of the surface in the x and y directions on the adopted hectometric (10²) scale. These slopes were obtained from a 1 : 10 000 scale map, with 5 m contour interval, based on aerial photographs taken in 1971. Altitude differences were measured over horizontal distances of 200 m. At any point, the steepest slope tan a and its azimuth A_α may then be calculated from:

(17)

With ρ denoting ice density and g denoting gravity (ρg = 0.088 bar m⁻¹), the equilibrium equations read:

(18)

When the x axis is oriented in the direction of the steepest slope, the new shear stress parallel to the surface is:

(19)

Because surface slopes are small, the difference between sines and tangents is negligible. Thus, if the two last corrective terms in Equations (18) are negligible, the classical relation ∂τ_{x ′z} /∂z = ρg sin α would result. This, however, is not the case: we shall see that the derivatives of the surface stresses are not negligible.

4.3. Strain triangles and stress triangles

To calculate strain rates from Equations (4), we need the first partial derivatives of functions u(x, y) and v(x, y), which are known only at a limited number of points. To obtain these, we use an interpolating function that is continuous everywhere, but within a triangle formed by three neighbouring stakes it is a linear function of x and y, so its first partial derivatives are uniform, namely:

(20)

To compute a, b, a′, b′, it is convenient to introduce the mean of the values of x_i and y_i at the three corners of a triangle, say x _G and y _G, and the mean of the velocities, say u _G and v _G.

(21)

Such triangles are called strain triangles. In the present study, their numerical names have three digits. The first two digits are the number of a stake at a corner; the third digit increases from west to east as for stake numbers. Strain triangles have already been used by other authors such as Hambrey and Müller (1978) and Hambrey and others (1980). Their strain triangles, however, are often of quite different sizes, and include some very acute or very obtuse angles.

The following objective procedure allows one to build strain triangles of similar size.

1. 1. The distance from every stake to its nearest neighbour is measured. Let d be the mean value of these distances. (For the net of 37 stakes of Figure 7, .)

2. 2. Next, draw all segments linking two stakes that are between and apart. When two such segments cross each other, the longer one is suppressed. A mosaic of strain triangles is thus obtained, along with, perhaps, some useless polygons. The range of triangle sides may be increased slightly if there are not enough strain triangles. In Figure 7 three additional triangles were obtained by raising the upper limit of from 274 m to 290 m.

Fig. 7 Stakes in 1972/73 (crosses), strain triangles (solid lines) and their centres of mass (circles) and stress triangles (dashed lines). Mames of stress triangles are given in Figure 11. Same orientation as Figure 2.

The surface stresses inferred from surface strain rates are considered to be uniform within each strain triangle. Nevertheless, these stresses may be used to estimate the x and y derivatives of stresses by assuming that the calculated stresses apply to the centres of mass of the strain triangles. Then, approximate values of the derivatives are calculated as above, assuming that they are constant within triangles having, as corners, the centres of mass of the strain triangles. These new triangles will be called stress triangles.

If all the centres of mass of the strain triangles were used to form a mosaic of stress triangles, the latter would be smaller (in the case of Figure 7, instead of 137.1 m), and hence more numerous. Furthermore, many of them would be too obtuse. This can be understood by considering the ideal case of a perfect net of stakes that yields equal equilateral strain triangles (Fig. 8).The centres of mass of the strain triangles form a mosaic of regular hexagons. Each of these hexagons may be divided into an equilateral stress triangle of the same size as the strain triangles, plus three smaller obtuse triangles. The obvious solution is to fuse three obtuse triangles from neighboring hexagons into a single equilateral triangle of the same size as the others. This means that many centres of mass of the strain triangles (one-half if the net of stakes had an infinite extent) must be dropped.

Fig. 8. Ideal stake net, with corresponding strain and stress triangles. The notation shown is used in the calculation of the mixed second derivative at the origin (Equation (22)).

The data for 1972/73 (Fig. 7) are not far from this ideal case. Fifty-one strain triangles are drawn from 37 stakes. Twenty-eight centres of mass out of 51 have been used to build 33 stress triangles. The number of output values is about the same as the number of input data. This is an essential precaution when correlations in the output are sought. By using a single analytical function to interpolate scalar data over many stakes, the number of output values could be increased at will, but since no mathematical handling can increase the quantity of information, most of the correlations in the output would be mathematical artifacts.

As shown by the following example, the direct calculation of stress gradients avoids the potentially ambiguous calculation of second derivatives of the velocity components. Consider the ideal case depicted in Figure 8, and calculate ∂ ²u/∂x∂y at the origin from the value at the origin (u ₀) and those at the six corners of the hexagon centred at the origin (u ₁ ,u ₂,…, u ₆). First ∂u/∂x and ∂u/∂y are calculated at points A, B, C around the origin (cf. Fig. 8).Then, from these values, it is found that at the origin (d denoting the distance between stakes):

(22)

The net of stakes surveyed from 1966 to 1972 is not so good because the main goal then was to measure mass balances along traverses. Therefore, on row 4 three stakes out of six are useless for the present study, whereas on row 3 the absence of a stake 33 and the loss of stake 36 are unfortunate. For studying variations between successive years the situation is worse because many stakes were not surveyed in all 7 years. We will compare the displacements in 1966/67, 1969/70 and 1972/73. If we replace stakes 35 and 37 with stakes 35bis and 37bis nearby, we then have 12 permanent stakes. These yield only eight acceptable strain triangles, and three acceptable stress triangles (Fig. 9).

Fig. 9. Strain and stress triangles constructed using stakes that lasted from 1966 to 1973.

4.4. Annual surface strains in 1972/73

Surface strain rates for 1972/73 (when data are most numerous) are displayed in Figure 10. The principal strain rate is drawn at the centres of mass of the strain triangles, but recall that strain rates are assumed to be uniform over the triangle. Except for triangle 656, is always the most compressive (negative) principal strain rate. The most extensive principal strain rate is either or . Only in the latter case is this strain rate shown in Figure 10. A pattern emerges in these strain rates. In the western and lower part of the area, ; there, most of the compression, , is balanced by horizontal extension. Elsewhere (except in triangle 255), most of is balanced by a vertical extension.

Fig. 10. Principal strain rates at the surface in 1972/73. Orientation and scale are as in Figures 2, 3 and 7. Thick line denotes compressive strain rate and dashed line, extending strain rate where it is larger than the strain rate normal to the surface. The monstar pattern is clearly seen. Dot-dash line is axis of the subglacial valley. Numbers on a dotted straight line are sites where faults were observed in 1957. Double thin lines are crevasses in August 1971.

The highest effective shear strain rates at the surface, and hence the lowest viscosities, η, are found in strain triangles 586, 588, 589 and 766, 767, 768, in the upper and eastern part of the ablation zone, where ice coming from the main accumulation area converges into a much narrower ice stream. There, η, given by Equations (6), (11) and (16), is about 10 bar a, the effective shear stress, τ, is about 0.5 bar, and σ_x is about −1 bar. Effective shear strain rates are low, and thus viscosity is high, in the six strain triangles 366–378 where the surface slope is fairly uniform (tan α = 0.15) and the thickness is 40–55 m. In triangle 377, τ = 0.270 bar and η ⁼ 31.2 bar a. In the five other strain triangles, τ ranges from 0.306 to 0.346 bar, and η from 24.3 to 19.0 bar a.

The lowest effective shear stress and highest surface viscosity (τ = 0.240 bar, η = 39.6 bar a) are found, isolated, at strain triangle 755 where the velocity is the fastest (14.4 m a⁻¹ average for 1965–73).With continuous derivatives (as in reality), at a point where both components of velocity are a maximum, strain rates must be zero. This is an isotropic point. Stable patterns of principal strain-rate trajectories have been discussed by Nye (1983). He has shown that the most frequent case in glaciers should be a “monstar” pattern around a single isotropic point. This is indeed the case in the ablation zone of Glacier de Saint-Sorlin, with the isotropic point in strain triangle 755.

An important question is to what extent strain rates (and hence deviatoric stresses) depend on the size of the strain triangles. To study this, strain rates have been recalculated with data from only 14 stakes (15 strain triangles) covering about the same area as the 51 strain triangles used above (Fig. 13a, shown later). Because power dissipation per unit volume is , the arithmetic mean of has been adopted for comparison of these two analyses. The 3/4 power of this arithmetic mean will be called the power average of .

In 1972/73, with 51 strain triangles this power average was 0.0280 a⁻¹. With 15 strain triangles it becomes 0.0254 a⁻¹. This difference is barely significant. However, the small influence of strain triangle size does not allow one to decrease the density of stakes. With the direction of principal stresses known at only 15 points, the monstar pattern is not clearly seen and the isotropic point is missed.

4.5. Crevasses and Faults: Flow Modes

Near-surface strain rates and stresses in 1972/73 will be used to suggest a tentative explanation for crevasses and faults in the ablation area. Theoretically, crevassing requires a tensile stress large enough to fracture ice. Because atmospheric pressure, which adds to all normal stresses, is omitted in all our calculations, it might be thought that the principal tensile stress must be much larger than 1 bar. However, fracture requires only a local and momentary stress, while the values computed above are averages on a hectometric and yearly scale. Moreover, after sunny days melting ice grains at the surface are actually already more or less separated by water films. Minute cracks already exist, and stresses are enhanced at the tips of these cracks. Therefore, the important factor is the extensional strain rate, which opens the crack. Here, the calculated annual values are pertinent. Fieldwork on crevasse formation has made little progress since the pioneering work of Meier (1958), Schram (1966), Ambach (1968) and Holdsworth (1969). These authors only studied systems of transverse crevasses, and only two of the five glaciers examined were temperate (Saskatchewan Glacier, Canada, and a tributary of Hintereisferner, Austrian Alps). According to Meier, crevassing requires a principal extensional strain > 1% a⁻¹, but Ambach thought that it must be >3% a⁻¹. In contrast, Hambrey and Müller (1978) found a lack of correlation between crevassing and the extensional strain rate.

The few small crevasses in the ablation zone of Glacier de Saint-Sorlin, as they appear on the aerial photographs of August 1971, are shown in Figure 10. The most important are the transverse crevasses between stakes 73 and 74. These formed in the accumulation zone, were bridged and hidden by snow, and are now closing ( reaches −2.31% a⁻¹ in strain triangle 733). Longitudinal crevasses form in triangles 342, 445, 555, 666 and 768. In all of these cases the following three conditions are met:

(23)

Among the triangles that satisfy the first condition, triangles 434 and 444 are excluded by the second. The third condition, which is justified below, excludes triangle 433, although it has the largest σ ₃ Among the 51 strain triangles, the only ones in which all three conditions are satisfied and in which, notwithstanding, no crevasses appear, are triangles 545 and 554, just upstream of triangle 555 in which there is crevassing. Since some small changes in the strain-rate field between 1971 and 1973 may be expected, this discrepancy does not disprove the crevassing conditions above.

The faults considered here are not the ones with conspicuous overthrusts that are often seen at the fronts of advancing glaciers (Lliboutry, 1965, plate LVIb; Post and LaChapelle, 2000, p. 44). In general, no surface displacement is apparent in the faults on Glacier de Saint-Sorlin, either because thrusting has ended or because its rate is much slower than the ablation rate. In old clean glacier ice, faults are revealed by impurities on the line along which the faults intersect the surface. Because there are no impurities in the actual fault plane, these impurities must have been carried by meltwater, which indicates that there must have been a small step along the fault-line. The upper side (hanging wall) can be removed by a single blow with an ice axe, exposing a very planar surface that dips 45–70° up-glacier. These faults are well described in Klebelsberg (1948–49, p. 62–69), and called in German Scherrissen (shear cracks). The only American author who mentions them is Goldthwait (1973).

I observed such faults on Glacier de Saint-Sorlin in August 1957 (Lliboutry, 1958,1965 (p.607–609)), but I did not look for them systematically. I studied them only along a straight traverse (dotted line in Fig. 10). Sites 1 and 2 (denoted A and B in 1958) are in strain triangle 555; sites 3 and 4 (formerly C and D) in triangle 445; and sites 5 and 6 (formerly E and F) in triangle 344. While Klebelsberg (1948–49) only mentions reverse faults, implying compression, I also observed normal faults, implying extension.

This raises an interesting question: why a normal fault, rather than a crevasse? This may be explained using the classical theory of Mohr’s envelope as a fracture criterion (cf., e.g., Lliboutry, 2000, ch. 12). According to this theory, the plane of fracture contains the direction of the intermediate principal stress. Several cases, which will be called modes as in fracture theory, are then possible. Crevassing will be denoted C, reverse faulting R, and normal faulting N. This symbol will be followed by Tor L depending on whether the feature at the surface tends to be transverse (perpendicular) or longitudinal (parallel) to the flow direction. Recall that in this paper a₂ is always normal to the surface and is zero.

σ ₁ < σ ₃ < σ ₂ (reverse faulting modes): If the compressive stress is large enough, there is fracture by shear, with a fault meeting the surface along the principal direction in which σ ₃ acts (modes RT and RL). Locally σ ₁ then drops, and the greatest compressive stress becomes σ ₃. If as is large enough, another reverse fault, in a perpendicular direction, may appear (mode RR).

σ ₁ < σ ₂ < σ ₃ (crevassing modes): The fracture plane must be vertical. If is large enough a crevasse opens (modes CT and CL). Then, locally, σ ₃ = 0 = σ ₂ and reverse faulting in the σ ₁ direction becomes possible (modes CTR and CLR).

σ ₁ < σ ₂ < σ ₃ (normal faulting modes): If as is large enough, there should be a normal fault cutting the surface in the σ ₁ direction (modes NT and NL). Then as drops and, if σ ₁ is large enough, a normal fault in the perpendicular direction may also appear (mode NN).

Thus, ten different modes are possible, whereas with the oversimplified two-dimensional glacier model, only modes RT (“compressive flow”) and CT (“extensive flow”) are possible. As shown in Table 4, in August 1957, at the six sites 1–6, I observed five distinct modes. At the same sites in 1972/73, only two modes are predicted. Thus, 16 years after my observations, a general increase in speed and retreat of the terminus have modified the flow modes. With the strain-rate–stress field of 1972/73, normal faults should not appear and reverse faults should be much more frequent.

Table 4. Flow modes (symbols are explained in text)

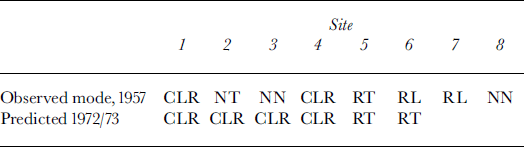
The formation of crevasses and faults explains why the effective shear stress at the surface never rises above 0.50 bar. In 43 strain triangles out of 51, it remains in the range 0.33–0.46 bar, and its modal value is 0.38 bar. To model glacier flow at the hectometric scale, a glacier may be considered as a perfectly continuous medium only below some critical value, τ _c, of the effective shear stress. Up to this value, it is non-linear viscous. When this value is reached, faulting makes the glacier behave like a perfectly plastic body. At the surface, τ _c is about 0.38 bar. I speculate that it should increase with pressure and become of order several bars at the bottom. Otherwise, microrelief would cause extensive faulting, and the sliding velocity would not be determined by the basal shear stress.

5. Driving Forces and Sliding

5.1. Shallow driving forces in 1972/73

The 33 stress triangles that can be constructed with the 1972–73 stake net are drawn in Figure 11. These form three stripes denoted L (left, looking downstream), M (middle) and R (right). In each stripe, they are numbered going downstream from 1 to 14, so that when two stress triangles in neighbouring stripes have a common side, they have the same number. Two triangles do not belong to these three stripes. According to the rule above, they are denoted LL13 and RR8.The directions of surface velocities (u _G, v _G) at the corners (x _G, y _G) of these stress triangles are indicated. Their azimuths are A _v = arctan(u _G/v _G).

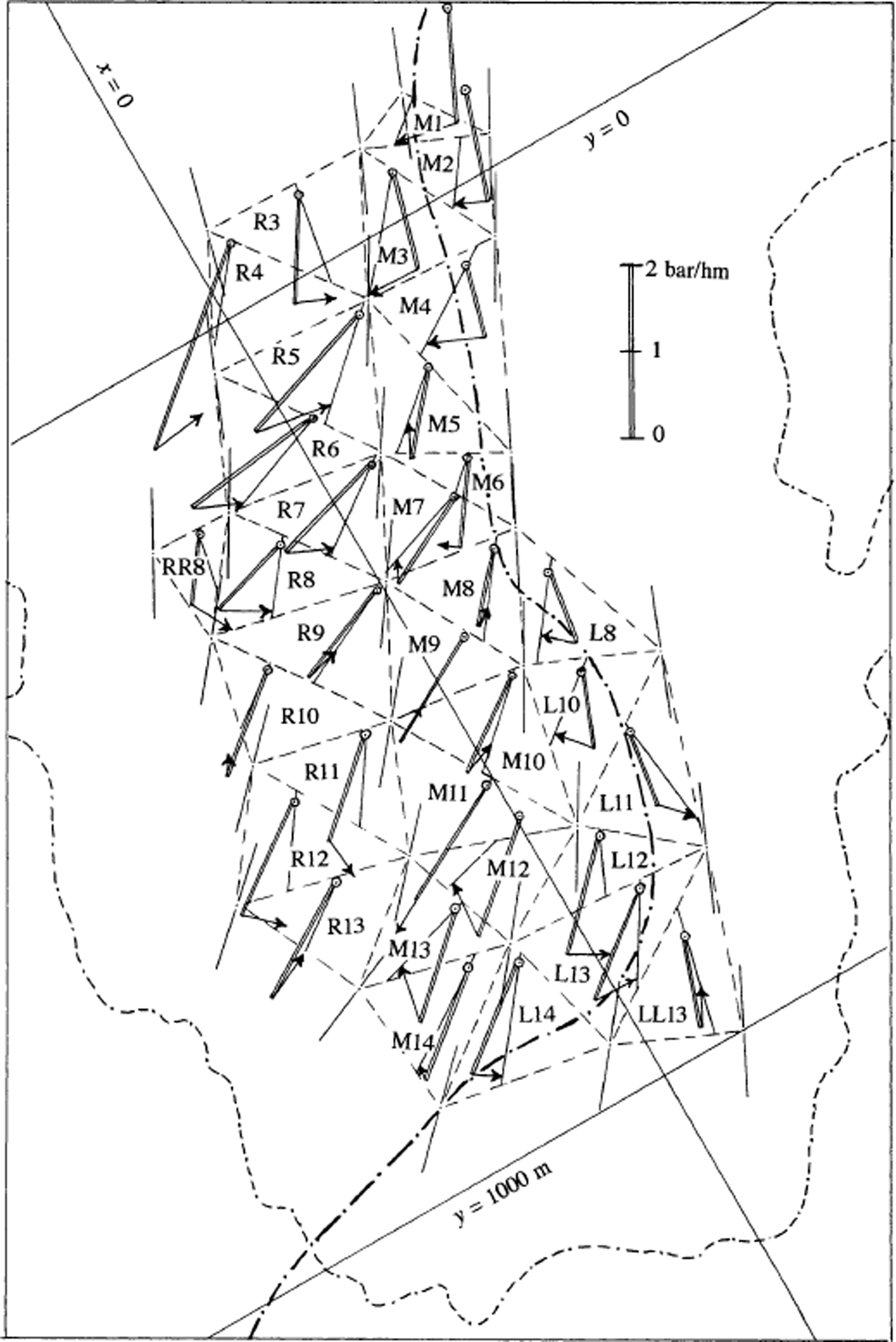
Fig. 11. Stress triangles for 1972/73. Velocity directions at the corners of the triangles (centres of mass of strain triangles) are indicated by thin lines. In each stress triangle the driving forces per unit volume at shallow depth are drawn. These are the components of gravity along the steepest slope (double line) and extra force due to stress gradients (arrow). The origin of this vector (small circles) is arbitrary, and chosen to make the figure clear. The azimuth of the resultant driving force, (Γ_x, Γ_y), is indicated by a line crossing the stress triangle. (The driving force is assumed to be uniform within each stress triangle) Orientation of map is as in Figures 2, 7 and 10.

At any depth, there is a gravitational driving force per unit volume parallel to the surface, with components (ρg sin α_x, ρg sin α_y ). This force is in the direction of the steepest surface slope, with azimuth A_α . At shallow depths, horizontal gradients of stresses yield an important corrective term, with components (δ_x , δ_y ) (cf. Equation (18)). The total driving force per unit volume, parallel to the surface, has the following components and azimuth:

(24)

The surface slope and the corrective terms (δ_x ,δ_y ) have been determined assuming that they are uniform within a given stress triangle. All of the data are displayed in Figure 11. Because our calculation of the stresses excludes smooth variations, the vectors (δ_x , δ_y ) are sometimes more or less opposite in adjacent stress triangles as, for example, in M3 and R3, L12 and M12, and L10 and L11.

Comparing, for each stress triangle, the azimuths (1) of the surface slope at its centre of mass (A_α ), (2) of the total driving force near the surface (A _s), and (3) of the mean surface velocity (mean of the velocities at the three corners of the triangle) (A _v), stress triangles may be classified as follows:

Group 1: A_s < A_v < A_α

L12, L13, L14 on the left; R3, M8, R11, R12, R13 on the right.

Group 2: A_α < A _v < A _s

M1, M2, M3, M4, L8, L10, M13, M14, along a central stripe.

Group 3: A _v < A _s, A_a

1. (a) A _s < A_α : R4, R5, R6, R7, R8, RR8, R9, M10

2. (b) A _s ≈ A_α : M9, M11

3. (c) A_α ≈ A _s: M5, M6, M7, R10, M12

Group 4: A _s < A_α < A _v

LL13, L11.

The usefulness of this classification will appear in section 5.3.

5.2. Friction and sliding velocity: approximations

The shear stress against the bed (hereinafter called the friction), the sliding velocity, and the sliding law that relates them, have no meaning if the relevant time- and spatial scales are not specified. With respect to the former, we are dealing, herein, with mean annual velocities and thus ignore variations on shorter time-scales. Therefore, we can, at best, only obtain an empirical sliding law that could not be inferred from theory and that does not take subglacial water pressures into consideration. With respect to spatial scales, herein the “bed” does not refer to the real interface between ice and rock, but rather to a smoothed surface (±5 m), with a smoothing length of 100–200 m, as mapped in Figure 3. The difference between the actual and the smoothed surfaces, termed the microrelief, includes bumps and crags up to 5 m high, possibly hollows up to 5 m deep, and possibly steps with a change in elevation of up to 10 m. In addition, near the terminus, as noted, there is about 1 m of loose debris between the ice and the rock. In the deglaciated forefield, “tails” of moraine in the lees of crags are very long. Similar features should exist beneath the glacier margin. All these unknown details, in addition to the local stresses and fluctuations of velocity that they provoke, are not considered. We are interested only in the mean friction and mean velocity. Herein, what are called “extra” bottom stresses and strain rates are the ones that are effective on a hectometric scale, and may be considered as uniform within every stress triangle.

The shear stress on a basal plane parallel to the surface has components τ_xz and τ _yz. These are not the same as the components of the friction, τ _bx and τ _by. τ _bx and τ _by represent the shear stress on the smoothed bed, which is not parallel to the surface. However, because the exposed microrelief does not show regular furrows and ridges in sound rock, and because the “tails” of loose debris follow the direction of the flow, it is assumed that the friction and the sliding velocity at any location are always in the same direction. Let us estimate the difference between these stresses.

Bed slopes in the x and y directions, denoted tan ß_x and tan ß _y , as well as surface slopes tan α _x and tan α_y , are assumed to be small. For the xy-plane to become the smoothed bed, the frame of reference must be rotated using a rotation matrix which for small angles can be approximated by:

(25)

The stress matrix Σ becomes Σ′ = ^t RΣR. In this way we find:

(26)

All the stresses and strain rates in this equation, as well as the viscosity, are values at the bottom and are unknown. If the strain rates involved in the corrective terms were the same as at the surface, they would be of order 10⁻² a⁻¹. Angles θ_x and θ_y are of order 10⁻¹. At the bottom, 2η < 10 bar a, and thus the corrective terms would be of order 10 ⁻² bar at most. In fact, however, there are extra bottom strain rates, and corrective terms as high as 0.1 bar should be possible. This is, nevertheless, much less than the probable values of τ_xz and τ_yz at the bottom (estimates below are in the range 0.4–0.9 bar). Therefore, to totally ignore the corrective terms and to assume τ _bx ≈ τ_xz , τ _by ≈ τ_yz should not introduce serious errors in the qualitative study below.

Another approximation will be made. Consider the relations:

(27)

Both of these quantities should equal 0.1–0.2 a⁻¹. Near the bed, the vertical velocity (relative to the surface) is:

(28)

w varies slowly in space, so |∂w/∂x| and |∂w/∂y| should be of order 10⁻²a⁻¹. These derivatives thus may be neglected in

Equation (27). With this approximation, putting the origin of the z axis at the bed:

(29)

The integrand is zero at the surface (z = h) and becomes large near the bottom. Because

(30)

an admittedly rough approximation is:

(31)

5.3. Bottom driving forces vs shallow driving forces

Two criteria may be used to show that, for a given stress triangle, the extra bottom driving forces are important and not related to the surface driving forces. (But the reverse is not true: these criteria may not necessarily be fulfilled, even where extra bottom driving forces, not related to surface forces, are important.)

First criterion: A _v is not included between A _α and A _s

At shallow depth (h − z), the extra driving force has components δ_x (h − z) and δ _y(h − z), which are known. If this extra driving force comes from horizontal stresses of distant origin that are transmitted at shallow depth, it should go through a maximum and vanish at larger depths. Then A _v ≈ A _α. If, on the contrary, it has a local cause at the bed, it should vary more or less as (h − z)η and remain important near the bottom. (It would be exactly so if the strain rates and were independent of depth.) Assuming that it does not vary at all, another limit for Av is found: A _v ≈ A _s. Thus, when A _v is not included between A _α and A _s, bottom extra driving forces are important and have a direction quite different from the surface driving forces.

According to the classification in section 5.1 above, important bottom extra driving forces exist in groups 3 and 4. The stress triangles of group 4, LL13 and L11, are the only ones on the western side of the subglacial valley. The 15 triangles of group 3 are on the eastern side of the subglacial valley, before it turns eastward. Thus the slopes on both sides of the subglacial valley cause important extra driving forces. These forces force the glacier flow closer to the south-north direction of the subglacial valley, deviating from the southwest-northeast direction of the steepest surface slope.

These bottom extra driving forces cannot be computed without adding some assumptions and simplifications that are questionable in this context. Even with these assumptions and simplifications, the computation must be done numerically and involves areas of increasing size as larger depths are considered (Van der Veen and Whillans, 1989). Therefore, it has not been attempted. To derive an empirical sliding law, without preconceived ideas about its form, the 17 stress triangles described above cannot be used.

Second criterion: A computation that ignores unknown bottom extra driving forces yields a negative sliding velocity

Assuming that no unknown driving forces appear near the bottom, Equation (29) can be integrated from the surface to the bottom. With the approximations discussed above, the friction τ _b is then included between and . Assuming that the shear stress parallel to the surface is the only deviatoric stress, a maximum value of the sliding velocity is obtained:

(32)

When both estimates of τ _b yield negative values for U_b, the starting assumption is wrong. Among the 16 remaining stress triangles, this applies to L12, M1 and M2, the only ones for which and are > 1.04 bar. These three triangles are in the subglacial valley, probably over slight adverse slopes that impede the flow.

5.4. Can an empirical sliding law be suggested?

The estimated upper and lower limits of τ _b and U_b, for the 13 stress triangles that remain, are plotted in Figure 12. For each triangle, the surface velocity adopted is the arithmetic mean of the values at the three corners. The two limits are linked by a straight line. A sliding law τ _b = τ _b (U_b) will be acceptable if its curve crosses most of the 13 segments.

Fig. 12. Attempt to find an empirical sliding law τ _b (U _b ), on the hectometric and annual scales. Straight segments link limits of (τ _b , U _b ) for each stress triangle. Dashed lines represent Equation (33) for different values of C.

The result is disappointing: no sliding law emerges from this figure. For example, a commonly assumed sliding law is of the form:

(33)

Such curves are drawn in Figure 12, with values of C ranging from 0.550 to 0.338 bar (m a⁻¹)^−1/3. Different laws are acceptable for 5 or at most 6 stress triangles out of 13. The reason for the failure involves much more than the roughness of the bed. The winter values of the effective pressure N, and the duration of the period with N ≈ 0 during the melt season are also important and should differ widely from one stress triangle to another.

5.5. Surface slope and friction on the terminal ice ramp

At a fixed point, the annual variation of the surface altitude is:

(34)

where h is the thickness and b is the mass balance (in m ice a⁻¹). As an application, consider point x = 241, y = 905. This point is the centre of mass of strain triangle 254 with corners at stakes 15, 23, 25 in 1972/73. This triangle was then at L = 230 m from the terminus, over the axis of the subglacial valley which has a very slight camber or saddle here. Thus the bed has a zero slope (β = 0, tan θ = tan α). At this point at the end of September 1972, h = 34 m, tan α = 0.18, and for strain triangle 254, in 1972/73, ε_zz = 0.0178 a⁻¹. As values of the surface velocity and of the annual balance, the means of the values at the corners are adopted: U _s = 4.44 m a⁻¹, and b = (−2.72 − 2.26 − 2.29) /3 = −2.42 m ice a⁻¹. Thus:

(35)

Equation (34) may be applied at the very terminus to determine the balance at that point from the rate of recession of the terminus, say . Using indices 0 for the values at the terminus, we have:

(36)

In 1972/73, , tan α ₀ = 0.27, and tan β ₀ = 0.105, so tan θ ₀ = 0.16. U ₀ is less than in the previous example because of the compressive strain in the direction of flow. If the strain rate of triangle 254 holds down to the terminus, U ₀ would be 0.3 m a⁻¹, but if the compressive strain decreases linearly to zero, U ₀ would be 2.4 m⁻¹. Thus: −2.22 ≤ b ₀ ≤ −2.56 m. Because the balance at stake 15 for 1972/73 was −2.72 m of ice, and the terminus was 50 m lower, a balance close to −3.0 m might be expected, but owing to drifting, the accumulation of snow, relative to the area-averaged snowfall, should be lower at the upper point and higher at the terminus where the slope changes from 0.27 on the terminal ice ramp to 0.105 ahead of it. Each year the accumulation of wind-blown snow flattens the ice ramp, which then becomes more convex in late summer. Weather is generally fine then, and ablation remains important. The ablation is caused mainly by a warm breeze ascending from the valley in the afternoons (Martin, 1975). The air cools as it flows over the glacier, so ablation is much higher close to the terminus. In mid-August 1971, mean surface slopes over successive 100 m segments, starting from the terminus, were (based on a 1 : 10 000 map drawn from aerial photographs): 0.225, 0.225, 0.170. At the end of September 1972 (based on an accurate survey) they were 0.270, 0.240 and 0.160.

The mean friction on the bed over the last 230 m can be estimated, assuming that the flow in the centre of the ice ramp is two-dimensional (no shear stresses on the sides impeding the motion), and that the bed is a plane with the same mean slope: tan β = (2656 − 2640)/230 = 0.070. The down-glacier normal stress acting at the upper end of this ice wedge is assumed to be, over the 34 m of thickness, the same as that computed at the surface:

(37)

With tan θ denoting an average of the values of θ at the upper and lower points (0.18 and 0.16, respectively), the forward equilibrium of the ice ramp reads:

(38)

(Note that this equation cannot be applied with L < 100 m because we are dealing with friction on a hectometric scale.) The mean sliding velocity, (U + U ₀)/2, lies between 2.4 and 3.4 m a⁻¹.This implies surprisingly low friction. From Figure 12, we might expect 0.7 ≤ τ _b ≤ 0.9 bar with this sliding speed. Reverse faults and overthrusts have not been observed and cannot explain the discrepancy. Separation should be extensive year-round, so these values of τ _b near the terminus could be compared with those in the remainder of the ablation zone during early summer, if they were known.

5.6. Changes in surface strain rates and driving forces from year to year

A complete computation of strain rates, viscosity, stresses and extra driving forces δ_x, δ_y due to horizontal stress gradients for different years has been done using measured stake velocities (as opposed to BLUE values). This has been done for 1966/67 (when the velocities were a minimum), 1969/70 (when they were a maximum) and 1972/73 (see Table 5). As noted, only five strain triangles and three stress triangles can be compared for these three years.

Table 5. Evolution with time of surface velocities and surface principal strain rates

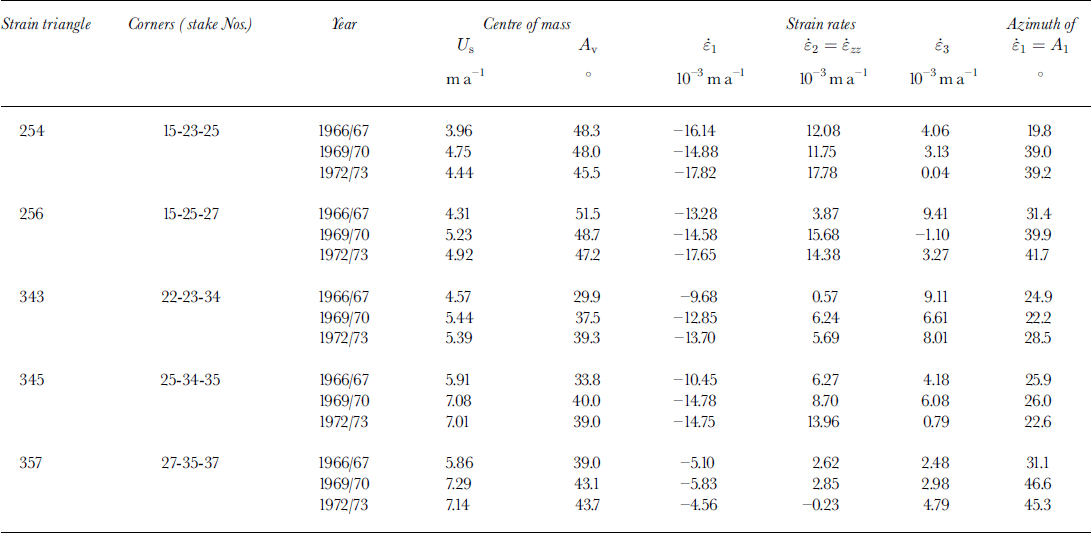
The evolution with time of surface extra driving forces (δ_x and δ_y ) is puzzling. The variations were of opposite sign, and in the same year were opposite in L14 and M14bis. In M13bis and M14bis, the behaviours of δ_x were roughly similar, while those of δ_y were not. There are too few stress triangles to obtain any general pattern that might lead to some deterministic explanation.

5.7. Comparison of strain rates in 1961/62 and 1972/73

Using the 1961/62 stake surveys, 15 strain triangles can be constructed. For the sake of comparison, the same number of strain triangles has been kept for 1972/73. While the 1966–73 data did not clearly show a decadal trend in the velocities, such a trend becomes apparent for 1961–73. The arithmetic mean of the surface velocities at the 15 centres of mass increased from 6.00 m a⁻¹ in 1961/62 to 8.13 m a⁻¹ in 1972/73. The power-averaged effective shear strain rate increased from 0.0170 a⁻¹ to 0.0254 a⁻¹, more or less in proportion. However, this quantitative comparison may be fallacious because the strain triangles are not the same. Therefore, the 15 principal strain rates for these two years have been drawn on the same figure (Fig. 13), placing them, as in Figure 10, at the centres of mass of the respective strain triangles.

Fig. 13. Comparison of surface strain rates in 1961/62 and 1972/73. (a, b) Respective strain triangles (schematic). (c) Principal strain rates, indicated as in Figure 10 (black = 1961/62; white = 1972/73). The fifth column of stakes (stakes 15–85) runs along the axis of the glacier.

Starting from the terminus and going upstream along the axis of the glacier (stake column 5), in 1972/73 the longitudinal compressive strain rate, , decreased continuously and vanished at the isotropic point, roughly at y = 0. In 1961/62, was smaller at the terminus by about one-half, but increased up-glacier, reaching its 1972/73 value at y = 500 m. In addition, there is a single datum on the axis, near y = −200 m, which seems to indicate that the isotropic point was there. Moreover, on the righthand side (stake column 7), there were large extending strain rates, , that had disappeared by 1972/73. Thus, from 1961/62 to 1972/73, with increasing velocities and terminus retreat, the lower part of the ablation zone became less extensive in the transverse direction, while the isotropic point probably moved down-glacier about 200 m. At this point, flowlines begin to diverge instead of converge. Thus a central stream of ice of given width in the glacier tongue tapped a wider area of the accumulation zone in 1973 than in 1962.

Further stake surveys on Glacier de Saint-Sorlin have been analyzed by Vincent and others (2000). Between 1972/73 and 1982/83 the continuous thinning of the ablation area, which had averaged −1.0 m a⁻¹ since 1952, stopped. Notwithstanding this, during this time period (and until 1984/85) velocities increased along the axis of the glacier (Vincent and others, 2000, fig. 6). In my opinion, this was not due to a decadal trend in the subglacial conditions, as suggested by these authors, but rather to a change in the flowlines. The lower part of the ice stream that they consider narrowed with time.

6. Conclusions

Let us restate the questions that have been answered, and recommend future studies that may further clarify them.

In the ablation zone, surface velocities fluctuate from year to year, both in intensity and in direction, in a random way. It is only for 1972/73, when the stake net contained 37 stakes, allowing analysis of 51 strain triangles with sides of 210–290 m, that the trajectories of principal strain rates are precise enough to show the monstar pattern clearly. The 15 strain triangles drawn from the 1961/62 data do not show such a pattern, but it seems that the isotropic point, where streamlines cease to converge and begin to diverge, was then about 200 m further upstream. This increase in the area of convergence with time may explain the tendency for velocities to increase between 1966/67 and 1984/85. Thus, to consider the mass balance of a central ice stream with fixed sides may be unsound.

By introducing the creep law for ice, determined in the laboratory, the stresses at shallow depth can be calculated for each strain triangle. Strain rates and stresses are pertinent to crevassing and faulting. While the classical two-dimensional glacier model leads to 2 flow modes (compressive or extensive), in real three-dimensional glaciers 10 flow modes must be distinguished. Five of these were observed in 1957. An explanation has been suggested for the observation that an extensional strain rate may cause either crevassing or normal faulting. It seems that, owing to crevasses and to normal and reverse faults, the effective shear stress (on the hectometric scale) cannot rise above some limiting value τ _c. When this value is reached, strain rates become undetermined, as in classical perfectly plastic bodies. It appears that a realistic value of τ _c at the surface is 0.38 bar. How τ _c increases at depth remains an unsolved problem.

Friction on the bed and the sliding velocity were sought for 33 stress triangles, but 20 of these were rejected because of proven but unknown extra driving forces acting near the bottom. Even so, no precise empirical sliding law can be suggested. An unknown and essential factor is the increase in area and in time of the zone with interconnected subglacial cavities, possibly accompanied by uplift, at the climax of the melting season. In any case, the very low friction near the terminus (τ _b ≈ 0.26 bar) is a further mystery.

It has been shown that the flow deviates from the direction of the steepest surface slope owing to extra bottom driving forces that arise from the shape of the bed. There are also extra driving forces at shallow depth; these forces can be inferred from the calculated surface stresses. These should be related, over most of the ablation zone, to flow conditions at the margins.

The implications of this study for future investigations of the dynamics of Alpine glaciers (I mean real glaciers, not the usual oversimplified models) seem to me essential. On a glacier of moderate length, given the wide spatial fluctuations of velocities and flowlines, a simple array of stakes along the axis of the glacier yields dubious results. Even at low velocities, a well-determined sliding law on the hectometric and annual scales does not exist. This fact impedes solution of the inverse problem, the determination of stresses and velocities at depth from surface data, even when the bed topography is well known. “Winter” dynamics and early-summer dynamics should be tackled separately. Moreover, to determine surface strain rates and stresses thoroughly, and thus to make the monstar pattern appear, a dense net of more than 30 stakes is required. (Of course the monstar pattern can always be made to appear with fewer stakes by using an interpolating analytical function, but then the monstar may well be a mathematical artifact.) Weeks of hard fieldwork are needed, distributed over three or four successive years.

To obtain a deterministic explanation for the stress fluctuations at shallow depth, the programme must include not only an annual survey of the limits of the glacier, but also data collected very close to the boundaries: particularly balances and surface slopes. The surface profile must be surveyed at the end of the ablation season because it becomes more convex in late summer. I am rather pessimistic about the chances that a thorough study of an Alpine glacier will be started again in the near future, but this last request might be included easily in instructions circulated by the World Glacier Monitoring Service.

Will all these programmes, exclusively grounded on terrestrial surveys, become obsolete with the development of synthetic aperture radar (SAR) interferometry? SAR allows one to measure diurnal velocities on large mountain glaciers with only limited fieldwork, and even in winter (Rabus and Fatland, 2000). It will make an invaluable contribution to the knowledge of glacier dynamics, but it has two drawbacks. First, it is not accurate enough for small glaciers or near the termini. On Black Rapids Glacier, Alaska, U.S.A., Rabus and Fatland measured surface velocities of 10–30 cm d⁻¹ with 10% uncertainty. On Glacier de Saint-Sorlin the range is 0.7–5 cm d⁻¹. Thus SAR interferometry gives no hope of interpreting available long-term records of annual advances or retreats of Alpine glaciers. Second, SAR interferometry only gives one component of the velocity, so temporal shifts in azimuth are not resolved. The surface strain rates and stresses at hectometric spatial scale cannot be inferred. Only precise terrestrial surveys and borings can solve the many problems thrown up by the present study.