Volume change of Jakobshavn Isbræ, West Greenland: 1985–1997–2007

Abstract

Following three decades of relative stability, Jakobshavn Isbræ, West Greenland, underwent dramatic thinning, retreat and speed-up starting in 1998. To assess the amount of ice loss, we analyzed 1985 aerial photos and derived a 40 m grid digital elevation model (DEM). We also obtained a 2007 40 m grid SPOT DEM covering the same region. Comparison of the two DEMs over an area of ∼4000 km² revealed a total ice loss of 160 ± 4 km³, with 107 ± 0.2 km³ in grounded regions (0.27 mm eustatic sea-level rise) and 53 ± 4 km³ from the disintegration of the floating tongue. Comparison of the DEMs with 1997 NASA Airborne Topographic Mapper data indicates that this ice loss essentially occurred after 1997, with +0.7 ± 5.6 km³ between 1985 and 1997 and −160 ± 7 km³ between 1997 and 2007. The latter is equivalent to an average specific mass balance of −3.7 ± 0.2 m a⁻¹ over the study area. Previously reported thickening of the main glacier during the early 1990s was accompanied by similar-magnitude thinning outside the areas of fast flow, indicating that the land-based ice continued reacting to longer-term climate forcing.

1. Introduction

Jakobshavn Isbræ (JI), West Greenland, drains 5.4% of the Greenland ice sheet (Rignot and Kanagaratnam, 2006) and is one of the largest of the ice sheet’s outlet glaciers (Fig. 1). Ice drains westward into an 800 m deep fjord via the south branch (SB) main-trunk glacier and the north branch (NB) tributary (Fig. 1). JI was in approximate equilibrium during the period 1964–97, with the terminus fluctuating 1–2 km about a seasonally averaged position (Pelto and others, 1989; Sohn and others, 1998; Csatho and others, 2008). Dramatic thinning of the outlet glacier began after 1997, and the subsequent retreat and speed-up of JI has been well documented (e.g. Thomas and others, 2003; Joughin and others, 2004, 2008; Krabill and others, 2004; Podlech and Weidick, 2004; Amundson and others 2008, 2010): speeds have more than doubled, the terminus has retreated >15 km, and total thinning along the lower reaches of the outlet glacier has exceeded 200 m. Although there are several reports of thinning rates from repeat NASA Airborne Topographic Mapper (ATM) flights, an accurate estimate of total ice loss since thinning and retreat began has been lacking. To obtain such estimates we utilized three sets of data: (1) a digital elevation model (DEM) derived from photogrammetric reanalysis of high-quality1985 high-elevation (∼13 500 m) aerial photographs, (2) 1997 NASA ATM data and (3) a DEM derived from 2007 SPOT-5 (Système Probatoire pour l’Observation de la Terre) imagery and obtained though the SPIRIT program (© Centre National d’Études Spatiales, France (CNES)). The aerial photos were flown on 24 July 1985 and were originally analyzed by Fastook and others (1995). We have reanalyzed these photo sets using digital photogrammetry (BAE SOCET SET^®) and significantly improved DEM quality and resolution. Our 40 m grid DEM then formed the basis for our comparison with 1997 ATM data and with the SPOT-5 2007 40 m grid DEM.

Fig. 1. Shaded relief composed from three flight-lines flown on 24 July 1985 using DEM with 40 m grid spacing. Coordinates are in UTM (km) (zone 22N) and contour intervals are 100 m. The south branch (SB) is the main-trunk outlet glacier and flows from the east into the fjord where it is joined by the north branch (NB) tributary to form a 12 km long floating tongue (FT). GCPs are indicated by red circles, ice-survey check points by blue squares. Photogrammetry degenerates at and above the snowline (∼1250 m) because of featureless snow. Dark boundary outlines area used for elevation difference map (Fig. 6). Dark circle marks the location of the ‘rumple’, R, a shallow area along the south fjord wall that apparently acted as a pinning point for the floating tongue during its period of stability.

2. Data

2.1. 1985 DEM

The original negatives of the 1985 aerial photos, flown on 24 July, are archived at Mark Hurd Inc. (Minneapolis). We obtained the camera calibration and 14 μm scans for our digital photogrammetry analysis. Fastook and others (1995) estimated pixel ground resolution at ∼2 m. We optimized photo contrast for glacier visibility and used BAE SOCET SET^® (BAE-SS) digital photogrammetry software, with its NGATE correlation strategy set for low contrast and moderate to low slope angles, and derived a 40 m grid DEM in a Universal Transverse Mercator (UTM) coordinate system (zone 22) with elevations referenced to height above ellipsoid (HAE; World Geodetic System 1984 (WGS84)). The photogrammetric model consisted of three photo strips, each containing eight photos with 60% along-flight overlap and ∼20% cross lap between strips. Tie points between stereo photo pairs were automatically determined by the software and then manually checked for accuracy. Bad points were discarded and new points acquired as needed to establish at least 20 well-distributed tie points for each photo pair. Additional tie points were identified on overlapping sections of the next along-flight photo and on cross-lapped portions of the three photo strips.

Surveyed ground control points (GCPs) were identified on the photos and used for aero-triangulation. The distribution of the control points is shown in Figure 1. Block adjustment of the stereo model was conducted after co-registering the GCPs and the tie points. GCP coordinates used to control the photogrammetric model were originally surveyed in 1985 by a University of Maine field party (Fastook and others, 1995; personal communication from H. Brecher, 2006) using Transit satellite Doppler positioning (TSDP). The GCP array consisted of seven points on land and seven points on ice. The land-based markers were still visible during our 2007–09 field campaigns and we resurveyed these points using precision GPS methods. The accuracy of the GPS-surveyed land GCPs is ±0.3 m. We found northing, easting and vertical differences of ∼1, −11 and −4 m respectively compared with the coordinates provided by H. Brecher. The reason for the differences is not known, although they may be related to coordinate transformations from the original reference system used in 1985 and UTM WGS84 (personal communication from H. Brecher, 2009).

Six of the seven land GCPs and five of the seven GCPs on ice are located in our model area (Fig. 1) and were used to control the model. We used our GPS-determined coordinates for the land GCPs to apply a translation to Brecher’s 1985 TSDP ice GCP coordinates and then used these positions for our photogrammetric analysis. TSDP surveys of GCPs 5 and 15 were done on the same day as the photo flight, but GCPs 7, 8 and 9 were surveyed about 10 days earlier. Brecher adjusted these GCP positions for ice motion by using TSDP surveys that were taken over a period of several days. Given the corrections made for coordinates, the estimated uncertainties for GCPs 5 and 15 are 0.6, 0.9 and 0.7 m for easting, northing and elevation, respectively, and slightly greater (1.0, 1.3 and 1.1 m) for GCPs 8 and 9 to account for uncertainty in ice motion. GCP 7 had the greatest uncertainties (3.6, 2.4 and 2.8 m) because of problems with TSDP surveys at that location.

The software automatically weights the GCPs according to uncertainty to control the positions and orientations of the photos. The BAE-SS reported root-mean-square model fit was ∼1.5 m. A shaded relief map based on the derived DEM is shown in Figure 1. Because of low contrast above the snowline, the DEM is unreliable above about 1250 m HAE.

2.2. 1997 NASA ATM

We used NASA ATM flights of Jakobshavn Isbræ to assess changes to the ice surface between 1985 and 1997. We acquired these datasets as ‘tiles’, or platelets, from W. Krabill (personal communications, 2008, 2009) and used the easting and northing flight-line coordinates of each tile to interpolate our 1985 DEM to determine changes in surface elevations. The coordinates provided for each tile are the center-point average of ∼900 laser returns within a square of ∼40 m, which is the grid size of our DEM. We chose 1997 as a baseline for this study for two reasons. The first is previous documentation that dramatic changes at JI began after 1997 (Thomas and others, 2003). The second is that the 1997 survey was the first detailed ATM flight of JI and was exceptionally dense, with flight-lines flown in a grid pattern separated by 5–10 km (Fig. 2). The database consists of ∼85 000 ATM nadir tiles over the area of ice in our 1985 DEM. Four flights were made, on 13, 15, 17 and 19 May 1997.

Fig. 2. 1985 orthophoto with 1997 ATM track lines. Coordinates are in UTM (km) (zone 22N). Colors indicate the change in elevation between 1985 and 1997 along the track line. Color bar is in meters. Areas near the glacier margin show the greatest degree of change and are treated as separate regions for the 1997 ATM profile-to-glacier extrapolations (numbered 1–4). Red contour denotes 700 m elevation, an arbitrary upper boundary for areas 1–4. Areas 1 and 3 show increases in elevation, while 2 and 4 show substantial thinning. Above 700 m elevation, the slight increases along the SB main-trunk glacier are offset by slight thinning elsewhere. Uncertainties are ∼±3 m near the terminus and ±6 m at higher elevations. Photogrammetry degenerates at and above the snowline (∼1250 m) because of featureless snow, and data above this level were not used in our calculations.

2.3. 2007 SPOT-5 DEM

We obtained SPOT-5 imagery and associated DEMs of JI for 24 July 2007 and 4 August 2007 under the SPIRIT (stereoscopic survey of Polar Ice: Reference Images and Topographies) Polar Dali Program (© CNES 2008). Details of the program and DEM processing are discussed by Korona and others (2009). Ground resolution of this imagery is 5 m along track and 10 m across track. The first set of imagery covers the terminus region while the second set covers most of the inland ice, with some overlap over the terminus. We merged the two DEMs and favored the 4 August DEM where overlap existed, because of its greater coverage of the glacier (Fig. 3). The SPIRIT DEMs are referenced to geoid EGM96 (Earth Gravity Model 1996). To facilitate comparison to the 1985 DEM and to the 1997 ATM, we converted the 2007 DEMs to HAE. We also masked some minor areas of cloud cover and excluded these areas from our analysis.

Fig. 3. Shaded relief mosaic composed from two SPOT-5 image flight-lines (24 July 2007 and 4 August 2007) using 40 m DEM. Coordinates in UTM (km) (zone 22N). (DEMs are courtesy of SPIRIT program (© CNES 2008, all rights reserved.) Region between slanted blue lines is region of image and DEM overlap. Grey and red lines are ATM tracks from 10 May 2007 and 20 September 2007 respectively. Red ATM lines mostly overlie blue ATM lines.

3. Uncertainties and Error Analysis

3.1. 1985 DEM

We assessed the accuracy of the 1985 DEM using various ground-truth datasets. These data are almost exclusively over land and are mostly our own kinematic and static GPS surveys, performed during annual field campaigns in 2006–09. We also included tiled ATM data (∼7% of the total points), filtered for slope roughness, to obtain better spatial distribution. We excluded land terrain where we knew the DEM failed to model the land surface. The results of comparing elevations at ∼9000 points showed a Gaussian distribution with a standard deviation σ _sd = 2.8 m and a slightly positive bias (0.7 m) (Fig. 4). Given these results and the close proximity of many of our ground-truth land points to the ice margins (<5 km), we assigned a random error of ±12.8 m per pixel for ice near the land boundary after adjusting for the systematic error of 0.7 m (Table 1). Unfortunately, we lack ground-truth data for the 1985 ice surface itself, except for several ice positions which were surveyed by TSDP within 2 weeks or less of the flights in 1985. We adjusted these positions for movement and estimate their accuracy at ±1 m. Comparison of these points to our DEM yielded σ _sd = 2.4 m, very similar to our land results. However, given the paucity of ground-truth points on ice and the greater uncertainties associated with the ice GCPs, we chose to use a conservative estimate for DEM uncertainty for elevations near the snowline: ±5.8 m, twice that of the land results (Table 1).

Table 1. Uncertainty estimates for the 1985 and 2007 DEMs (σ _SD) and for elevation differences, ΔZ, between the DEMs (σ _ΔZ ). σ _SD for individual DEMs are from Figures 4 and 5. σ _ΔZ was calculated by standard propagation of uncertainties

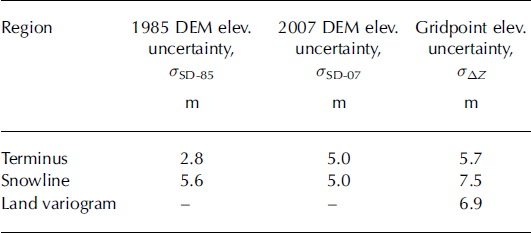
Fig. 4. Data distribution and Gaussian fit for elevation difference between 1985 DEM and ground-truth points for land areas adjacent to glacier. The latter are mostly from kinematic GPS, but about 7% (blue bars) are from the ATM.

3.2. 2007 DEM

Korona and others (2009) used Ice, Cloud and land Elevation satellite (ICESat) data obtained in late March 2007 (1411 points) and late October 2007 (1428 points) to assess the accuracy of their DEM and reported that the SPIRIT DEM was within ±6 m of ICESat for 90% of the data. We used three additional datasets to further assess the accuracy of the SPIRIT DEM: (1) our GPS kinematic land surveys and ATM data over land areas; (2) ATM data from 10 May 2007 (14 500 points); and (3) ATM data from 20 September 2007 (19 900 points). The latter two datasets were used to interpolate elevations on the 2007 DEM over the glacier regions at the ATM easting and northing coordinates. These 2007 ATM data contain an order of magnitude more points and are closer in time to actual imagery dates than the ICESat data used by Korona and others (2009). The results of our assessments are shown in Figure 5. The comparison to land surveys shows a reasonable Gaussian distribution, with a mean of 1.6 m and σ _sd = 4.7 m (Fig. 5a).

Fig. 5. (a) Distribution of elevation differences between 2007 DEM and GPS ground-truth points over land areas adjacent to the glacier. (b) Comparison of 2007 SPOT DEM with 2007 ATM data. Red points are for ATM tracks flown 10 May 2007. Blue points are for 20 September 2007 ATM. (c) Distribution of elevation differences for glacier ATM tracks minus 2007 DEM.

Figure 5b plots ΔZ, the elevation difference between both ATM flights and the SPOT DEM, as a function of elevation, Z. Two trends are discernible: data for the 10 May flights tend to plot positive (red) while those for the 20 September flights are more negative (blue). These trends are consistent with ablation, flight paths and dynamic thinning of the glacier. Annual ablation ranges from ∼4 m at 100 m to zero at the equilibrium-line altitude (ELA; ∼1250 m) (Echelmeyer and others, 1992). The SPOT imagery was acquired approximately in the middle of the ablation season, which typically begins in May and ends by late September. Thus, the seasonal differences in ablation help to explain the trends in Figure 5b but only up to ∼2 m. With some ΔZ as much as 20 m, some other factor must be at play and we believe this to be ice dynamics. We note that the 2007 ATM data, particularly for lower elevations, are mostly over ice streams. JI continued to exhibit seasonal oscillations and dramatic summer retreats, often several kilometers in length, well into 2007 (Joughin and others, 2008; Amundson and others, 2010). In particular, inspection of available Landsat images for the summer of 2007 (http://glovis.usgs.gov) shows that the terminus retreated about 2 km between 14 May and 2 August (date of the second SPOT image), and retreated another 0.5–1.0 km by 25 August (the last Landsat image available for the summer of 2007). As the SB retreated, the tongue disintegrated, ice speeds increased and seasonal variations in velocity at the terminus became pronounced (Luckman and Murray, 2005). In 2007 the velocity near the calving front varied from a low of 22 m d⁻¹ in winter to a high of 27 m d⁻¹ in summer, with the change roughly synchronous with the 8 km seasonal fluctuation in terminus position that year (Joughin and others, 2008). Changes in dynamic thinning associated with these seasonal velocity oscillations are most pronounced at and near the terminus and can strongly affect the elevation profiles (Amundson and others, 2010). We therefore believe that the trends in ΔZ at lower elevations (Fig. 5b) reflect these seasonal trends in terminus position and dynamic thinning of the main-trunk ice stream.

We combined the two ATM ΔZ datasets in order to estimate the accuracy of the 2007 DEM (Fig. 5c), noting that the effects of ablation and ice dynamics roughly cancel each other in the combined dataset. The distribution of ΔZ in Figure 5c is non-Gaussian, making the use of standard deviation problematic. We therefore also show the inter-quartile range (IQR) as another estimate of the uncertainty. The median and the mean of the dataset are nearly identical to those we found for ΔZ over land (Fig. 5a and c), thus providing further evidence for a positive bias. Considering all the datasets, including Korona and others (2009), we decided to adjust the 2007 DEM for a positive bias of ∼1.7 m and use a conservative value of ±5 m as a measure of uncertainty of the 2007 DEM after removing this bias (Table 1).

3.3. Uncertainty of elevation comparisons

3.3.1. 1985 DEM versus 2007 SPOT DEM

We now address the question of estimating the uncertainty (or standard error) when comparing our two DEMs to determine volume change and geodetic mass balance. The total change in ice volume is determined by differencing the DEMs and summing gridpoints over the ∼4000 km² area of DEM overlap. Implicit in this method is the assumption that bed elevations remained constant over the interval. The volume change can in turn be converted to mass (water equivalent (w.e.)) if the ice density is known, and further converted to an area-wide mass balance by dividing by the area.

When estimating the uncertainty of such calculations, two extreme approaches have commonly been applied (see Rolstad and others, 2009, for a review). One approach uses the uncertainty of point measurements (i.e. the standard deviation of the elevation error) to represent the integrated uncertainty: the point uncertainty is essentially treated as being totally correlated across the area of integration (e.g. Cox and March, 2004; Larsen and others, 2007). Other authors (e.g. Thibert and others, 2008) estimate uncertainties in glacier volume change by assuming spatially uncorrelated (or totally random) elevation errors. In this case, uncorrelated integrated errors will be a factor n ^1/2 smaller than correlated errors, where n is the number of gridpoints over which the spatial integration is carried out (Rolstad and others, 2009). For example, for datasets with a grid resolution of 10 m, applied over an integration area of 100 km², the difference is a factor of >100.

Nuth and others (2007) and Rolstad and others (2009) argued that spatial correlation of the elevation differences in the DEMs strongly influences the integrated uncertainty of volume change and geodetic mass balance. In their method, the spatial covariance of the two DEMs is assessed by the use of variograms to determine correlation length. In this approach, a grid of elevation differences, derived from comparing two different DEMs over land adjacent to the glacier, are analyzed for both standard deviation and to determine correlation length through use of variograms. The correlation length is then taken as a measure of data correlation between the two DEMs over the ice. If elevations are independently measured concurrently over the glacier, then statistical information from these differences can be used to aid uncertainty estimates.

We have opted to use the spatial correlation approach to assess the standard error in our volume calculations, as a good compromise between the two extremes. To obtain variograms, we first differenced the two DEMs over the adjacent land areas, which are sparsely vegetated and devoid of bushes and trees. We then determined the spatial correlation length over this area using standard variogram software and following methods outlined by Rolstad and others (2009). We note three differences between the land and glacier surfaces in our study area. (1) The image contrast is different over land and rocks vs blue ice and snow, and all areas have a varying degree of sun and shadows. Images used in both DEMs were optimized for contrast over the glacier surface. This optimization resulted in a higher degree of shadows and darkened terrain for land areas, which are also steeper than the glacier surface. (2) Both DEMs were also optimized for low slope angles, representative of the glacier surface. The surface slope of the glacier in our study area is mostly low-angle: <5° for ∼90% of the ice surface. In contrast, the adjacent land area has a mean slope of ∼11°, with some slopes as steep as 60–70°. An inaccurate horizontal position can lead to larger errors in the elevation differences for steeper areas, so elevation difference errors may be larger for the land than for the glacier. (3) In general, the glacier surface is smoother than the land surface, and with the same spatial resolution the elevation-difference error over land may be larger than for the glacier. Thus, uncertainties derived using correlation lengths determined over adjacent land are apt to be a conservative estimate for the ice surface.

The elevation-difference (ΔZ) data over land surfaces were filtered for outliers before variograms were derived. These outliers mostly consisted of points where (1) one or the other DEM failed to model the land surface, (2) gridpoints fell into shadow zones and (3) the terrain was steep (>15°). Support for this data filtering comes from calculation of the standard deviation of the remaining data points, which gave 6.9 m. This value is reasonably close to 5.7 m, the uncertainty determined by using standard propagation of error and the values of standard deviations over land for each DEM (Table 1).

We used a spherical model to fit the data in our variogram and found a correlation length, L, of 500 m, zero nugget, and a sill height (or variance), C, of 47.5 m². The equivalent correlation area, A _c, is then given by

(1)

In our case, the glacier area, A, is much greater in scale than the correlation length. For these conditions, the variance of the mean of A is given by

(2)

(Rolstad and others, 2009). The choice for σ _ΔZ is somewhat subjective. The variogram gives σ _ΔZ = C ^1/2 = 6.9 m, based on the statistics of our filtered ΔZ dataset. In contrast, propagation of error using standard deviations derived in section 3 suggests that σ _ΔZ = 5.7 m for ice near the terminus regions and 7.5 m for elevations near the snowline. As a conservative compromise, we chose to use 7.5 m to represent σ _ΔZ for the entire 4000 km² area of overlap covered by the DEMs. The results for σ _ΔA and σ_V are given in Table 2 where σ_V , the uncertainty in total volume change, is given by

(3)

and where the uncertainty for A is negligibly small (<1%) compared with the other uncertainties. The relatively small value for σ_V (0.19 km³) is a direct consequence of using the correlated length analysis and a very large area of integration (A ≫ A _c). For comparison, the result for σ_V if the point uncertainty is treated as being totally correlated across the area of integration is over two orders of magnitude greater, ±30 km³.

Table 2. Uncertainty estimates for total volume change between 1985 and 2007. σ _ΔA was computed from Equation (2) using 7.5 m for the gridpoint uncertainty, σ _ΔZ

One further adjustment is commonly examined in geodetic calculations: changes in ice- and firn-density profiles between DEM dates. Most studies invoke Sorge’s law, which assumes that in steady-state conditions the snow/firn/ice density profile is constant through time (Bader, 1954). In our case, the snowline is either nearly at (1985) or slightly above (2007) our highest DEM elevations, so elevation changes are composed completely of ice at a single density of 0.91 kg m⁻³ (cf. Lüthi and others, 2002, for JI ice density).

3.3.2. 1985 DEM versus 1997 ATM

The reported accuracy of the ATM data is ±0.3 m. Because the ATM flights were flown in mid-May 1997 and the 1985 aerial photography was flown on 24 July 1985, adjustments need to be made to account for seasonal changes. The terminus of the floating tongue was ∼2 km farther down-fjord in mid-May 1997 compared with 24 July 1985. We believe that the difference in position is attributable to the summertime seasonal retreat of the floating tongue, which was on the order of 2–4 km during this period (Sohn and others, 1998; Csatho and others, 2008). We therefore do not use ATM data beyond the 1985 terminus of the floating tongue when computing elevation changes.

Echelmeyer and Harrison (1990) found that there was no apparent change in seasonal velocity of the floating tongue in 1985. Luckman and Murray (2005) reported a detectable but very modest seasonal velocity variation in 1997. Given that seasonal velocity variation for both years was either nonexistent or comparatively small, we assume that any difference in elevation due to seasonal ice dynamics is negligibly small. Furthermore, the floating tongue was 10–12 km long in both 1985 and 1997. Any seasonal dynamics that did exist should have had little effect on surface elevations over a floating tongue. This is in contrast to 2007, when an extended floating tongue no longer existed and when significant seasonal differences were documented at lower elevations along the SB main-trunk outlet glacier (Fig. 5b; Joughin and others, 2008).

The second adjustment we consider is for seasonal ablation. We again used ablation data from Echelmeyer and others (1992) and assumed that the ablation season began by mid-May and was midway through by 24 July. We then adjusted the computed elevation differences between the 1997 ATM data and the 1985 DEM accordingly. We estimate that the uncertainty in this adjustment is relatively small, probably <0.3 m.

Using standard propagation of errors, the uncertainty in any point elevation difference, ΔZ, is dominated by the uncertainty in the 1985 DEM: σ _ΔZ (85–97) = 2.8 m for ice near the terminus, ranging to 5.6 m for elevations near the snowline.

3.3.3. Methods used to estimate volume change between 1997 and 1985

A method for glacier-wide extrapolation of ATM data must be invoked when attempting to derive a volume change and geodetic mass balance by comparing ATM data to DEMs. We follow methods developed by Arendt and others (2002, 2006) in extrapolating 1997 ATM data to represent the glacier-wide area. For JI, our study area is well covered by 1997 ATM tracks (Fig. 2), which help make our glacier-wide extrapolation reasonably accurate.

We used our 1985 DEM to obtain the hypsometry of the glacier, which we classed into 100 m bins, H_z. For each bin, volume change was calculated by multiplying the average ΔZ _85–97 for that elevation bin by the glacier area for that bin. In areas where ΔZ showed different patterns over the glacier, we treated each area independently. In both cases, the measured average, ΔZ _ave, was assumed to be representative of all areas for that elevation. Because there are multiple ATM tracks at all elevations, we used the standard deviation of ΔZ _85–97 for each elevation bin to estimate the standard error associated with ΔZ _ave to represent that particular elevation bin, H_z.

We then used the standard deviation in point elevation differences and the standard error of ΔZ _ave for each elevation bin to obtain an estimate of the total uncertainty involved in the glacier-wide ATM extrapolation to the 1985 DEM volume calculations. Unfortunately, we have no good method of estimating a ‘correlation length’ for our ATM to DEM comparisons since ATM data over adjacent land are too sparse to develop a suitable DEM. In order to bracket the uncertainties involved in the ATM vs DEM volume change estimate, we first treated both uncertainties as totally correlated across the areas to derive a value for ‘maximum’ uncertainty. As discussed above, we believe that this method can significantly overestimate the uncertainty in volume change. At the other end, we evaluate the ‘minimum’ uncertainty by assuming that the point elevation error is totally random (uncorrelated) but that the standard error for ΔZ _ave is correlated for each H_z. A further discussion of this error analysis and a table of results (Table 5) are given in the Appendix. Table 3 summarizes the results reported in Table 5.

Table 3. Summary of volume changes and uncertainties for four areas near the glacier margin (to 700 m elevation) and for 100 m elevation bins above 700 m derived by comparing extrapolations of 1997 ATM profiles with the 1985 DEM. Details of statistics can be found in the Appendix (Table 5)

4. Results

4.1. 1985 DEM versus 2007

We differenced the 2007 and 1985 DEMs over the contiguous area of overlap to determine total ice volume change and to generate a map of surface elevation change (Fig. 6; Table 4). The equivalent in terms of eustatic sea-level rise (ESLR) (assuming ρ _ice = 910 kg m⁻³; Lüthi and others, 2002) for loss of non-floating ice is also given in Table 4 for comparison purposes. The eastern boundary in Figure 6 was dictated by lack of 1985 DEM reliability above the snowline (∼1250 m HAE). The northern and southern boundaries in Figure 6 correspond to the limits of the 1985 and 2007 DEMs. We segregated ice lost by the break-up of the floating tongue, as this loss does not contribute to sea-level rise. The latter was calculated by assuming hydrostatic equilibrium (Motyka and others, unpublished information), with uncertainties mainly a function of assumptions on ice and sea-water densities. We included in this calculation ice between the 1985 grounding line and the 2007 outlet glacier terminus because (1) these regions were at or near flotation and (2) they then became inundated with sea water as the terminus retreated. Loss of ice over grounded regions was 106.8 ±0.2 km³ compared with 53 ± 4 km³ from the disintegration of the floating tongue. The total volume of ice lost was 160 ± 4 km³; the ESLR equivalent of the grounded portion is 0.27 ± 0.00 mm. The annual area-averaged w.e. loss is 1.65 ± 0.04 m a⁻¹. However, as we discuss later, most of the ice loss between 1985 and 2007 essentially occurred between 1997 and 2007.

Table 4. Summary of volume changes and uncertainties over study area derived by differencing (1) 1985 and 2007 DEMs, and (2) 1985 DEM and 1997 ATM data

Fig. 6. Change in surface elevation between 1985 and 2007. UTM coordinates in km (zone 22N). The largest losses occur along the main outlet glaciers, but significant losses also occur along ice-sheet margins terminating on land. Comparison of 1985 DEM with 1997 NASA ATM data indicates that most if not all of this ice loss occurred between 1997 and 2007.

Figure 6 shows that most of the ice loss is focused in and around the major outlet glaciers. The greatest change in surface elevation occurs in the grounding region of the SB, with up to 275 m of total thinning. However, significant thinning occurs along the entire length of the SB outlet glacier and is ∼25 m at the eastern limit of our map (elevation ∼1250 m HAE). Elsewhere, away from the outlet glaciers, surface-elevation changes drop to <7.5 m, below our level of uncertainty, except along the western ice margins, as discussed below. The floating ice tongue thinned, calved and disintegrated after 1997 and accounts for about one-third of the total ice loss in our analysis. (The floating tongue in 1997 was ∼1000 m thick at the grounding line and tapered to about 550 m at the terminus.)

Pronounced thinning occurred in two other settings. The first is at the termini of minor outlet glaciers entering seawater fjords north and south of the main fjord, with thinning of 80–90 m (Figs 1 and 6). The other setting occurs just inland along the land-based ice margins north and south of the main outlet glaciers, with changes of 60–80 m (Fig. 6).

Certain additional features stand out. (1) The pattern of ice loss over the floating tongue helps define the position of the grounding zone in 1985 as distinguished by yellow and red on the floating tongue between 549.5 and 550 km easting in Figure 6. The brick red boundary to the east defines the position of the 2007 terminus. (2) 100–130 m of ice was lost over the feature termed the ‘Rumple’ by other investigators (Echelmeyer and others, 1991; Figs 1 and 6). This feature is a shallow area along the south fjord wall that apparently acted as a pinning point for the floating tongue during its period of stability from 1964 to 1997 (Echelmeyer and others, 1991; Thomas and others, 2003). (3) Another feature is the apparent demarcation of flowlines on the outlet glaciers (Figs 1 and 3) as well as on the elevation change map (Fig. 6). Gudmundsson (2003) suggested that appearance of flowlines on outlet glaciers is related to the fact that faster flow makes basal topography more transparent, leading to the formation of flow stripes. Accelerating flow will thus lead to the accentuation of flow stripes, which can then show up in difference maps that span a period of glacier acceleration.

4.2. 1985 DEM versus 1997 ATM and comparison with 2007 DEM

Figure 7 presents the results of directly comparing ∼85 000 1997 ATM tiles with our 1985 DEM. The ATM flight-lines are shown in Figure 2. The comparison indicates that there was little or no change in surface elevations between 24 July 1985 and the mid-May 1997 ablation-corrected ATM data for elevations above 700 m. However, the story for lower elevations is more complex: two divergent trends are evident in Figure 7, indicating that some areas of the lower glacier were thickening while others were thinning. When we plot these points on the 1985 orthophoto (Fig. 2), we find that points showing thickening are mainly confined to the outlet glaciers while thinning occurs principally in terminal regions away from the outlet glaciers. Both Thomas and others (2003) and Csatho and others (2008) used repeat ATM and reported ice thickening near the grounding line between 1985 and 1997. However, neither reported the thinning of ice in other regions that we document here.

Fig. 7. Comparison of elevation differences between 1985 and 1997 along ATM track lines as function of 1997 surface elevation. Track lines are plotted in Figure 2. Two divergent trends are apparent below 700 m. In contrast, little or no change in elevation is apparent above 700 m. Uncertainties are ∼±3 m near the terminus and ±6 m at higher elevations.

The results of our profile to glacier volume-change analysis are given in Table 3, with further details in the Appendix. Based on the discussion in the previous paragraph, we somewhat arbitrarily used 700 m elevation as the dividing line between terminus regions experiencing significant elevation changes, divided that region into four areas (Fig. 2) and then analyzed them separately. Regions above 700 m were treated as being relatively homogeneous. Inspection of Figure 2 indicates that this is not quite the case, with slight thickening of ice along the SB and slight thinning in regions outside the ice stream. However, the two tend to balance each other and, in any event, the differences above 700 m are near our limits of uncertainty. The standard deviation and skewness of the ΔZ distribution for each of the elevation bins are given in the Appendix (Table 5). We used the average of σ_{v -max} and σ_{v -min} as our estimate of uncertainty. In most cases, σ_{v -max} and σ_{v -min} did not differ substantially since the uncertainties tend to be dominated by the standard error of ΔZ _ave.

Integrating over the entire study area, the glacier registered an insignificant increase in volume (0.7 ± 5.6 km³) between 1985 and 1997, although there were some significant differences near the terminus. Locally, significant glacier thickening occurred over the SB outlet glacier terminus region (area 3 = 5.1 ± 1.8 km³), while pronounced ice loss occurred in areas 2 and 4: 1.8 ± 0.5 and 2.4 ± 0.5 km³, respectively (Table 3). Net volume changes at higher elevations were all similar to or less than the uncertainties.

Given the latter results, we can assess the total volume loss between 1997 and 2007, ΔV _97–07, by differencing ΔV _85–97 from ΔV _85–07. The result, 160 ± 7 km³ (Table 4), is equivalent to an average mass balance of −3.7 ± 0.2 m a⁻¹ over what is essentially the ablation area for the ice stream. At a local level, we compared the 1997 ATM data with the 2007 DEM and found elevation changes (thinning rates) of −232 ± 15 m (23.2 ± 0.5 m a⁻¹) near the SB 2007 terminus and −36 ± 5 m (3.6 ± 0.5 m a⁻¹) at 1250 m elevation of SB. Away from SB at higher elevations, thinning progressively drops to below uncertainty level at distances of ∼25 km from the main SB flow.

5. Discussion

The contiguous area of our DEMs spans an area of 4000 km². In comparison, Rignot and Kanagaratnam (2006) estimated that the area of the entire drainage basin is 92 000 km². Thus our analysis only covers a small proportion (6%) of the entire drainage basin. However, we note that our annualized total net ice loss, −14.6 ± 0.6 km³ w.e. a⁻¹ for 1997–2007, is close to the net mass-balance estimates made by Rignot and Kanagaratnam (2006) of −12.5 ± 4 km³ for 2000 and −16 ± 3.8 km³ for 2005, for the entire drainage basin. Thus, the ice lost over our comparatively small analyzed area appears to account for the majority of ice loss from JI since 1997. Much of the thinning is associated with SB, the main-trunk outlet glacier, with thinning rates of 3.6 ± 0.5 m a⁻¹ extending to the eastern edge of our analysis, about 60 km from the 2007 glacier terminus. Drawdown along the outlet glacier also occurred at higher elevations as reported by Pritchard and others (2009). Their analysis of 2003 vs 2007 ICESat data showed surface lowering of −0.8 ± 0.3 m a⁻¹ at ∼1600 m elevation (120 km from the glacier front). In contrast, the rate was −0.07 ± 0.22 m a⁻¹ over neighboring areas at similar altitude but outside the main glacier drainage.

Our annualized (1997–2007) estimate of ESLR contribution of 0.027 ± 0.007 mm a⁻¹ is ∼10% of the total contribution from the entire Greenland ice sheet, of 0.28 ± 0.04 mm a⁻¹ as determined by Luthcke and others (2006) from Gravity Recovery and Climate Experiment (GRACE) satellite measurements for the period 2003–05. This comparison with GRACE indicates that the changes at JI are indicative of the larger-scale changes occurring in Greenland.

Although the exact causes of the large ice losses at JI after 1997 are still a matter of debate, we believe they are primarily due to ocean–glacier interactions and dynamic effects. As discussed by Holland and others (2008), an increase in ocean temperatures after 1997 likely caused an increase in submarine melting of the floating tongue, which in turn destabilized it. Motyka and others (unpublished information) present evidence that changes in sea-water temperatures entering the fjord can have a direct, significant and rapid effect on the termini of the major JI outlet glaciers by changing the rates of submarine melting of the floating tongue. The thinning of the floating tongue by submarine melting and the subsequent loss of buttressing then led to an acceleration of ice flow and the break-up of the ice tongue. A dramatic increase in dynamic thinning ensued, as documented by Thomas and others (2003), Rignot and Kanagaratnam (2006) and Joughin and others (2008). Ocean effects are also likely responsible for terminus ice losses at the minor outlet glaciers. For ice margins away from the outlet glaciers, ice losses may be a continuation of forcing trends that were already underway between 1985 and 1997. In addition, they may be due to redirection of inland ice flow towards the main outlet glaciers as a result of upstream drawdown.

We note that the glacier margin experienced divergent trends between 1985 and 1997: thickening along the main-trunk outlet glacier and thinning in regions away from it.

The cause of the thickening is a matter of debate. The thinning we document elsewhere along the terminus argues that it is not related to an increase in mass balance. One explanation for the observed thickening is again ocean–glacier interactions. Data from conductivity–temperature–depth (CTD) measurements near the fjord entrance indicate a period of relatively constant temperature existed during the 1980s followed by a cooling trend in sea-water temperature from 1991 to 1996 (Motyka and others, unpublished information). The cooler sea-water temperatures will have reduced the rate of bottom melting, thereby allowing the tongue to thicken. The increased buttressing, in turn, will have led to thickening of ice in the region of the grounding zone and farther upstream. In contrast, we believe that terminal regions not directly affected by the ice tongue continued to thin in response to long-term atmospheric and other forcing.

6. Conclusions

Our analysis and interpretations of high-resolution DEMs and ATM data provide additional evidence that ice loss from JI since 1997 is primarily due to ocean forcing and dynamic thinning, and not atmospheric forcing. The 1985 aerial photos have become increasingly important for documenting and understanding the dynamic state of this outlet stream prior to the rapid retreat and for documenting the massive ice losses after 1997. Our analysis also shows the importance of both the NASA ATM and the SPOT-5 SPIRIT programs as sources for continued documentation of glacier changes worldwide.