Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T08:26:00.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of normal and shear strain on magnetic anisotropy energy of hcp cobalt: An ab initio study

Published online by Cambridge University Press:  17 June 2013

Juan Wang ,
Jan-Michael Albina ,
Tomio Iwasaki ,
Hiroshi Moriya  and
Yoshitaka Umeno
Juan Wang*
Affiliation:
Institute of Industrial Science, The University of Tokyo, Tokyo 153-8505, Japan; andDepartment of Mechanical Engineering, The University of Tokyo, Tokyo 113-8656, Japan
Jan-Michael Albina
Affiliation:
Institute of Industrial Science, The University of Tokyo, Tokyo 153-8505, Japan
Tomio Iwasaki
Affiliation:
Advanced Simulation Department, Hitachi Research Laboratory, Hitachi, Ltd., Hitachinaka, Ibaraki 312-0034, Japan
Hiroshi Moriya
Affiliation:
Advanced Simulation Department, Hitachi Research Laboratory, Hitachi, Ltd., Hitachinaka, Ibaraki 312-0034, Japan
Yoshitaka Umeno
Affiliation:
Institute of Industrial Science, The University of Tokyo, Tokyo 153-8505, Japan
*
a)Address all correspondence to this author. e-mail: ouken@ulab.iis.u-tokyo.ac.jp
Get access

Abstract

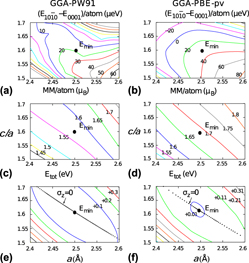
The magnetic anisotropy energy (MAE) of the bulk hcp Co under mechanical deformation is calculated by ab initio density functional theory (DFT) calculations based on the projector augmented wave method. We present a thorough investigation with respect to the choice of exchange-correlation functionals. The generalized gradient approximation (GGA) succeeds in predicting the easy axis of magnetization but underestimates the MAE in comparison to the experimental value, whereas the local density approximation gives a wrong magnetic easy axis. The DFT+U method offers an alternative to increase the MAE value. Unfortunately, as the MAE reaches the experimental value, strong distortions of the lattice parameters are observed. Our results with GGA suggest that a simultaneous reduction of the c/a ratio and increase of the lateral lattice parameter a will strongly enhance the MAE of the material, as observed experimentally. We also found that the MAE in hcp Co is reduced by shear strain.

Type
Articles
Information
Journal of Materials Research , Volume 28 , Issue 12 , 28 June 2013 , pp. 1559 - 1566
Copyright
Copyright © Materials Research Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Weller, D. and Moser, A.: Thermal effect limits in ultrahigh-density magnetic recording. IEEE Trans. Magn. 35, 4423 (1999).CrossRefGoogle Scholar
Lee, C.H., He, H., Lamelas, F.J., Vavra, W., Uher, C., and Clarke, R.: Magnetic anisotropy in epitaxial Co superlattices. Phys. Rev. B 42, 1066 (1990).CrossRefGoogle ScholarPubMed
Inaba, N., Nakamura, A., Yamamoto, T., Hosoe, Y., and Futamoto, M.: Magnetic and crystallographic properties of CoCrPt thin films formed on Cr–Ti single crystalline under layers. J. Appl. Phys. 79, 5354 (1996).CrossRefGoogle Scholar
Futamoto, M., Inaba, N., Nakamura, A., and Honda, Y.: Microstructures and basic magnetic properties of co-based epitaxial magnetic thin films. Acta Mater. 46, 3777 (1998).CrossRefGoogle Scholar
Shimatsu, T., Okazaki, Y., Sato, H., Kitakami, O., Okamoto, S., Aoi, H., Muraoka, H., and Nakamura, Y.: Large uniaxial magnetic anisotropy of Co–Pt perpendicular films induced by lattice deformation. IEEE Trans. Magn. 43, 2995 (2007).CrossRefGoogle Scholar
Andersson, G. and Hjörvarsson, B.: Effects of strain on magnetic anisotropy in Fe-and Co-based heterostructures. Phase Transitions 81, 679 (2008).CrossRefGoogle Scholar
Shimatsu, T., Okazaki, Y., Sato, H., Muraoka, H., Aoi, H., Sakurai, T., Okamoto, S., Kitakami, O., Tanii, S., and Sakuma, A.: Uniaxial magnetic anisotropy in Co and Co–Pt based perpendicular films in relation to lattice deformation. J. Appl. Phys. 103, 07F524 (2008).CrossRefGoogle Scholar
Wang, J-J., Sakurai, T., Oikawa, K., Ishida, K., Kikuchi, N., Okamoto, S., Sato, H., Shimatsu, T., and Kitakami, O.: Magnetic anisotropy of epitaxially grown Co and its alloy thin films. J. Phys. Condens. Matter 21, 185008 (2009).CrossRefGoogle ScholarPubMed
Paige, D.M., Szpunar, B., and Tanner, B.K.: The magnetocrystalline anisotropy of cobalt. J. Magn. Magn. Mater. 44, 239 (1984).CrossRefGoogle Scholar
Daalderop, G.H.O., Kelly, P.J., and Schuurmans, M.F.H.: First-principles calculation of the magnetocrystalline anisotropy energy of iron, cobalt, and nickel. Phys. Rev. B 41, 11919 (1990).CrossRefGoogle ScholarPubMed
Trygg, J., Johansson, B., Eriksson, O., and Wills, J.M.: Total energy calculation of the magnetocrystalline anisotropy energy in the ferromagnetic 3d metals. Phys. Rev. Lett. 75, 2871 (1995).CrossRefGoogle Scholar
Brooks, M.S.S.: Calculated ground state properties of light actinide metals and their compounds. Physica B & C 130, 6 (1985).CrossRefGoogle Scholar
Eriksson, O., Brooks, M.S.S., and Johansson, B.: Orbital polarization in narrow-band systems: Application to volume collapses in light lanthanides. Phys. Rev. B 41, R7311 (1990).CrossRefGoogle ScholarPubMed
Beiden, S.V., Temmerman, W.M., Szotek, Z., Gehring, G.A., Stocks, G.M., Wang, Y., Nicholson, D.M.C., Shelton, W.A., and Ebert, H.: Real-space approach to the calculation of magnetocrystalline anisotropy in metals. Phys. Rev. B 57, 14247 (1998).CrossRefGoogle Scholar
Stiles, M.D., Halilov, S.V., Hyman, R.A., and Zangwill, A.: Spin-other-orbit interaction and magnetocrystalline anisotropy. Phys. Rev. B 64, 104430 (2001).CrossRefGoogle Scholar
Xie, Y. and Blackman, J.A.: Magnetocrystalline anisotropy and orbital polarization in ferromagnetic transition metals. Phys. Rev. B 69, 172407 (2004).CrossRefGoogle Scholar
Burkert, T., Eriksson, O., James, P., Simak, S.I., Johansson, B., and Nordström, L.: Calculation of uniaxial magnetic anisotropy energy of tetragonal and trigonal Fe, Co, and Ni. Phys. Rev. B 69, 104426 (2004).CrossRefGoogle Scholar
Ono, F. and Maeta, H.: Determination of lattice parameters in hcp cobalt by using x-ray bond’s method. J. Phys. Colloq. 49, 8 (1988).CrossRefGoogle Scholar
Kresse, G. and Hafner, J.: Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).CrossRefGoogle ScholarPubMed
Kresse, G. and Furthmüller, J.: Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).CrossRefGoogle ScholarPubMed
Blöchl, P.E.: Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).CrossRefGoogle ScholarPubMed
Perdew, J.P. and Wang, Y.: Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244 (1992).CrossRefGoogle ScholarPubMed
Perdew, J.P., Burke, K., and Ernzerhof, M.: Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).CrossRefGoogle ScholarPubMed
Monkhorst, H.J. and Pack, J.D.: Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188, (1976).CrossRefGoogle Scholar
Dudarev, S.L., Botton, G.A., Savrasov, S.Y., Humphreys, C.J., and Sutton, A.P.: Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study. Phys. Rev. B 57, 1505 (1998).CrossRefGoogle Scholar
Mattsson, A.E., Armiento, R., Schultz, P.A., and Mattsson, T.R.: Nonequivalence of the generalized gradient approximations PBE and PW91. Phys. Rev. B 73, 195123 (2006).CrossRefGoogle Scholar
Yang, I., Savrasov, S.Y., and Kotliar, G.: Importance of correlation effects on magnetic anisotropy in Fe and Ni. Phys. Rev. Lett. 87, 216405 (2001).CrossRefGoogle ScholarPubMed
Wu, R. and Freeman, A.J.: Spin–orbit induced magnetic phenomena in bulk metals and their surfaces and interfaces. J. Magn. Magn. Mater. 200, 498 (1999).CrossRefGoogle Scholar
Steiner, M.M., Albers, R.C., and Sham, L.J.: Quasiparticle properties of Fe, Co, and Ni. Phys. Rev. B 45, 13272 (1992).CrossRefGoogle ScholarPubMed
Perdew, J.P., Chevary, J.A., Vosko, S.H., Jackson, K.A., Pederson, M.R., Singh, D.J., and Fiolhais, C.: Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671 (1992).CrossRefGoogle ScholarPubMed
Jansen, H.J.F.: Origin of orbital momentum and magnetic anisotropy in transition metals. J. Appl. Phys. 67, 4555 (1990).CrossRefGoogle Scholar
Wang, J., Albina, J-M., and Umeno, Y.. Ab initio calculation of strain effect on the magnetic properties of the thiogermanate [(CH3)4N]2FeGe4S10. J. Phys. Condens. Matter. 24, 245501 (2012).CrossRefGoogle ScholarPubMed
Černý, M., Pokluda, J., Šob, M., Friák, M., and Šandera, P.: Ab initio calculations of elastic and magnetic properties of Fe, Co, Ni, and Cr crystals under isotropic deformation. Phys. Rev. B 67, 035116 (2003).CrossRefGoogle Scholar
Ogata, S., Umeno, Y., and Kohyama, M.: First-principles approaches to intrinsic strength and deformation of materials: Perfect crystals, nano-structures, surfaces and interfaces. Modell. Simul. Mater. Sci. Eng. 17, 013001 (2009).CrossRefGoogle Scholar
Friák, M., Šob, M., and Vitek, V.: Ab initio calculation of phase boundaries in iron along the bcc-fcc transformation path and magnetism of iron overlayers. Phys. Rev. B 63, 052405 (2001).CrossRefGoogle Scholar
Shimada, T., Ishii, Y., and Kitamura, T.: Ab initio study of magnetism at iron surfaces under epitaxial in-plane strain. Phys. Rev. B 81, 134420 (2010).CrossRefGoogle Scholar
Moroni, E.G., Kresse, G., Hafner, J., and Furthmüller, J.: Ultrasoft pseudopotentials applied to magnetic Fe, Co, and Ni: From atoms to solids. Phys. Rev. B 56, 15629 (1997).CrossRefGoogle Scholar
Bagayoko, D. and Callaway, J.: Lattice-parameter dependence of ferromagnetism in bcc and fcc iron. Phys. Rev. B 28, 5419 (1983).CrossRefGoogle Scholar
Honda, Y., Funamono, H., Hasegawa, S., Kawasaki, T., Kugiya, F., Koizumi, M., Yoshida, K., and Tonomura, A.: Recorded magnetization patterns of highly c-axis oriented Co-Cr film observed by electron holography. J. Phys. Colloq. 49, C8–C1969 (1988).CrossRefGoogle Scholar
Bernards, J.P.C., Schrauwen, C.P.G., and Luitjens, S.B.: Single-layer and multilayered films for perpendicular recording based on a Co-Cr alloy. Appl. Phys. A 49, 491 (1989).CrossRefGoogle Scholar
Xu, J., Furukawa, M., Nakamura, A., and Honda, M.: Mechanical demagnetization at head disk interface of perpendicular recording. IEEE Trans. Magn. 45, 893 (2009).Google Scholar