Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T11:17:56.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Role of Cr-d states in the electronic and optical properties of the CdCr2X4 (X = S, Se) normal ferromagnetic spinels using PBE+U and TB-mBJ potentials

Published online by Cambridge University Press:  08 May 2017

Saurabh Samanta  and
Sapan Mohan Saini
Saurabh Samanta
Affiliation:
Physics Department, National Institute of Technology, Raipur 492010, Chhattisgarh, India
Sapan Mohan Saini*
Affiliation:
Physics Department, National Institute of Technology, Raipur 492010, Chhattisgarh, India
*
a)Address all correspondence to this author. e-mail: smsaini.phy@nitrr.ac.in
Get access

Abstract

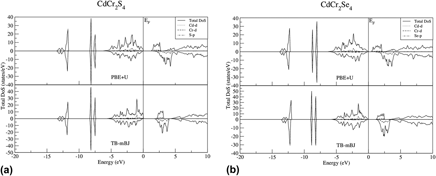
We have investigated theoretically the role of Cr-d states in the electronic and optical properties of the CdCr2X4 (X = S, Se) normal ferromagnetic spinels using the framework of an all-electron full-potential linearized augmented plane wave method. The calculations are performed using Coulomb corrected Perdew–Burke–Ernzerhof (PBE+U) and Tran–Blaha modified-Becke–Johnson (TB-mBJ) approximations with the adding of spin–orbit coupling in both schemes. The lattice parameters have been optimized and are in agreement with the existing experimental values. We found band gap values 1.606 eV and 0.972 eV of CdCr2X4 (X = S, Se), respectively, using the TB-mBJ scheme. Analysis of the site and momentum projected densities shows that the larger splitting of Cr-d states is responsible for the larger band gap by the use of the TB-mBJ scheme. Optical properties along the directions of lattice constants are studied on the basis of band to band transitions. We found the isotropic nature of the optical properties. Reflectivity stays low up to 1.6 eV, consistent with the energy gaps obtained using the TB-mBJ scheme in both the compounds. The refractive index, n(ω), and the extinction coefficient, k(ω), are also studied by the PBE and the TB-mBJ schemes.

Keywords

electronic structuremagnetic propertiesoptical properties
Type
Articles
Information
Journal of Materials Research , Volume 32 , Issue 12 , 28 June 2017 , pp. 2431 - 2437
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Amit Goyal

References

REFERENCES

Ahmad, I., Amin, B., Maqbool, M., Muhammad, S., Murtaza, G., Ali, S., and Noor, N.A.: Optoelectronic response of GeZn2O4 through the modified Becke–Johnson potential. Chin. Phys. Lett. 29, 097012 (2012).CrossRefGoogle Scholar
Semari, F., Khenata, R., Rabah, M., Bouhemadou, A., Omran, S.B., Reshak, A.H., and Rached, D.: Full potential study of the elastic, electronic, and optical properties of spinels MgIn2S4 and CdIn2S4 under pressure effect. J. Solid State Chem. 183, 2818 (2010).CrossRefGoogle Scholar
Dekkers, M., Rijnders, G., and Blank, D.H.A.: ZnIr2O4, a p-type transparent oxide semiconductor in the class of spinel zinc-d 6-transition metal oxide. Appl. Phys. Lett. 90, 021903 (2007).CrossRefGoogle Scholar
Kim, H.J., Song, I.C., Sim, J.H., Kim, H., Kim, D., Ihm, Y.E., and Choo, W.K.: Electrical and magnetic properties of spinel type magnetic semiconductor ZnCo2O4 grown by reactive magnetron sputtering. Solid State Commun. 129, 627 (2004).CrossRefGoogle Scholar
Mizoguchi, H., Hirano, M., Fujitsu, S., Takeuchi, T., Ueda, K., and Hosono, H.: ZnRh2O4: A p-type semiconducting oxide with a valence band composed of a low spin state of Rh3+ in a 4d6 configuration. Appl. Phys. Lett. 80, 1207 (2002).CrossRefGoogle Scholar
Wei, X., Chen, D., and Tang, W.: Preparation and characterization of the spinel oxide ZnCo2O4 obtained by sol–gel method. Mater. Chem. Phys. 103, 54 (2007).CrossRefGoogle Scholar
Bouhemadou, A., Zerarga, F., Almuhayya, A., and Omran, S.B.: FP-LAPW study of the fundamental properties of the cubic spinel CdAl2O4 . Mater. Res. Bull. 46, 2252 (2011).CrossRefGoogle Scholar
Yousaf, M., Saeed, M.A., Isa, A.R.M., Shaari, A., and Aliabad, H.A.R.: Electronic band structure and optical parameters of spinel SnMg2O4 by modified Becke–Johnson potential. Chin. Phys. Lett. 29, 107401 (2012).CrossRefGoogle Scholar
Dixit, H., Saniz, R., Cottenier, S., Lamoen, D., and Partoens, B.: Electronic structure of transparent oxides with the Tran-Blaha modified Becke–Johnson potential. J. Phys.: Condens. Matter 24, 205503 (2012).Google ScholarPubMed
Amini, M.N., Dixit, H., Saniz, R., Lamoen, D., and Partoens, B.: The origin of p-type conductivity in ZnM2O4 (M = Co, Rh, Ir) spinels. Phys. Chem. Chem. Phys. 16, 2588 (2014).CrossRefGoogle ScholarPubMed
M. Stoica and C.S. Lo: p-Type zinc oxide spinels: Application to transparent conductors and spintronics. arXiv: 1312.1728v1.Google Scholar
Zerarga, F., Bouhemadou, A., Khenata, R., and Omran, S.B.: Structural, electronic and optical properties of spinel oxides ZnAl2O4, ZnGa2O4 and ZnIn2O4 . Solid State Sci. 13, 1638 (2011).CrossRefGoogle Scholar
Amin, B., Khenata, R., Bouhemadou, A., Ahmad, I., and Maqbool, M.: Opto-electronic response of spinels MgAl2O4 and MgGa2O4 through modified Becke–Johnson exchange potential. Phys. B 407, 2588 (2012).CrossRefGoogle Scholar
Sharma, Y. and Srivastava, P.: Electronic, optical and transport properties of α-, β- and γ-phases of spinel indium sulphide: An ab initio study. Mater. Chem. Phys. 135, 385 (2012).CrossRefGoogle Scholar
Singh, D.J., Rai, R.C., Musfeldt, J.L., Auluck, S., Singh, N., Khalifah, P., McClure, S., and Mandrus, D.G.: Optical properties and electronic structure of spinel ZnRh2O4 . Chem. Mater. 18, 2696 (2006).CrossRefGoogle Scholar
Singh, N. and Schwinggenschlogl, U.: ZnIr2O4: An efficient photocatalyst with Rashba splitting. Europhys. Lett. 104, 37002 (2013).CrossRefGoogle Scholar
Samanta, S. and Saini, S.M.: Full potential study of electronic and optical properties of transparent oxide ZnCo2O4 by use of PBE and TB-mBJ potentials. J. Electron. Mater. 48, 3659 (2014).CrossRefGoogle Scholar
Landolt-Börnstein: Magnetic and other properties of oxides and related compounds. In New Series, Vol. III/4b, Hellwege, K-H., ed. (Springer, Berlin-Heidelberg, 1970).Google Scholar
V. Samohvalov: PAC investigations of ferromagnetic spinel semiconductors. Ph.D. Dissertation, The Technical University of Freiberg (2003).Google Scholar
Park, Y.D., Hanbicki, A.T., Mattson, J.E., and Jonker, B.T.: Epitaxial growth of an n-type ferromagnetic semiconductor CdCr2Se4 on GaAs (001) and GaP (001). Appl. Phys. Lett. 81, 1471 (2002).CrossRefGoogle Scholar
Nikiforov, K.G.: Magnetically ordered multinary semiconductors. Prog. Cryst. Growth Charact. Mater. 39, 1–104 (1999).CrossRefGoogle Scholar
Lee, T.H., Coburn, T., and Gluck, R.: Infrared optical properties and Faraday rotation of ferromagnetic HgCr2Se4 . Solid State Commun. 9, 1821 (1971).CrossRefGoogle Scholar
Shanthi, S., Mahadevan, P., and Sarma, D.D.: Electronic band structure of cadmium chromium chalcogenide spinels: CdCr2S4 and CdCr2Se4 . J. Solid State Chem. 155, 198 (2000).CrossRefGoogle Scholar
Wang, Y-H.A., Gupta, A., Chshiev, M., and Butler, W.H.: Half-metallic electronic structures of quaternary ferromagnetic chalcospinels: Cd x Cu1−x Cr2S4Cd x Cu1−x Cr2S4 and Cd x Cu1−x Cr2Se4Cd x Cu1−x Cr2Se4 . Appl. Phys. Lett. 92, 062507 (2008).CrossRefGoogle Scholar
Fennie, C.J. and Rabe, K.M.: Polar phonons and intrinsic dielectric response of the ferromagnetic insulating spinel CdCr2S4 from first principles. Phys. Rev. B: Condens. Matter Mater. Phys. 72, 214123 (2005).CrossRefGoogle Scholar
Ohgushi, K., Okimoto, Y., Ogasawara, T., Miyasaka, S., and Tokura, Y.M.: Magnetic, optical and magneto-optical properties of spinel-type ACr2X4 (A = Mn, Fe, Co, Cu, Zn, Cd; X = O, S, Se). J. Phys. Soc. Jpn. 77, 034713 (2008).CrossRefGoogle Scholar
Tran, F. and Blaha, P.: Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 102, 226401 (2009).CrossRefGoogle ScholarPubMed
Koller, D., Tran, F., and Blaha, P.: Merits and limits of the modified Becke–Johnson exchange potential. Phys. Rev. B: Condens. Matter Mater. Phys. 83, 195134 (2011).CrossRefGoogle Scholar
Reshak, A.H., Kamaruddin, H., and Auluck, S.: Acentric nonlinear optical 2,4-dihydroxyl hydrazone isomorphic crystals with large linear, nonlinear optical susceptibilities and hyperpolarizability. J. Phys. Chem. B 116, 4677 (2012).CrossRefGoogle Scholar
Reshak, A.H., Kamaruddin, H., Kityk, I.V., and Auluck, S.: Dispersion of linear, nonlinear optical susceptibilities and hyperpolarizability of C11H8N2O (o-methoxydicyanovinylbenzene) crystals. J. Phys. Chem. B 116, 13338 (2012).CrossRefGoogle ScholarPubMed
Madsen, G.K.H., Blaha, P., Schwarz, K., Sjostedt, E., and Nordstrom, L.: Efficient linearization of the augmented plane-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 64, 195134 (2001).CrossRefGoogle Scholar
Sjostedt, E., Nordstrom, L., and Singh, D.J.: An alternative way of linearizing the augmented plane-wave method. Solid State Commun. 114, 15 (2000).CrossRefGoogle Scholar
Schwarz, K., Blaha, P., and Madsen, G.K.H.: Electronic structure calculations of solids using the WIEN2k package for material sciences. Comput. Phys. Commun. 147, 71 (2002).CrossRefGoogle Scholar
Anisimov, V.I., Zaanen, J., and Andersen, O.K.: Band theory and Mott insulators: Hubbard U instead of Stoner. Phys. Rev. B: Condens. Matter Mater. Phys. 44, 943 (1991).CrossRefGoogle Scholar
Anisimov, V.I., Solovyev, I.V., Korotin, M.A., Czyzyk, M.T., and Sawatzky, G.A.: Density-functional theory and NiO photoemission spectra. Phys. Rev. B: Condens. Matter Mater. Phys. 48, 16929 (1993).CrossRefGoogle ScholarPubMed
Hohenberg, P. and Kohn, W.: Inhomogeneous electron gas. Phys. Rev. 36, 864 (1964).CrossRefGoogle Scholar
Blaha, P., Schwarz, K., Madsen, G.K.H., Kvasnicka, D., and Luitz, J.: WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. Universitat WIEN, Austria, 2001).Google Scholar
Perdew, J.P., Burke, K., and Ernzerhof, M.: Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).CrossRefGoogle ScholarPubMed
Monkhorst, H.D. and Pack, J.D.: Special points for Brillouin-zone integrations. Phys. Rev. B: Condens. Matter Mater. Phys. 13, 5188 (1976).CrossRefGoogle Scholar
Blochl, P.E., Jepson, O., and Anderson, O.K.: Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B: Condens. Matter Mater. Phys. 49, 16223 (1994).CrossRefGoogle ScholarPubMed
Yaresko, A.N.: Electronic band structure and exchange coupling constants in ACr2X4 spinels (A = Zn, Cd, Hg; X = O, S, Se). Phys. Rev. B: Condens. Matter Mater. Phys. 77, 115106 (2008).CrossRefGoogle Scholar
Sato, K.: Crystal growth and characterization of magnetic semiconductors. In Advances in Crystal Growth Research, Sato, K., Furukawa, Y., and Nakajima, K., eds. (Elsevier, Amsterdam, 2001); pp. 303–309.CrossRefGoogle Scholar
Zhao, H.B., Ren, Y.H., Lupke, G., Hanbicki, A.T., and Jonker, B.T.: Band offsets at CdCr2Se4–(AlGa)As and CdCr2Se4–ZnSe interfaces. Appl. Phys. Lett. 82, 1422 (2003).CrossRefGoogle Scholar
Santos-Carballal, D., Roldan, A., Grau-Crespo, R., and De Leeuw, N.H.: First-principles study of the inversion thermodynamics and electronic structure of FeM2X4 (thio) spinels (M = Cr, Mn, Co, Ni; X = O, S). Phys. Rev. B: Condens. Matter Mater. Phys. 91, 195106 (2015).CrossRefGoogle Scholar
Wooten, F.: Optical Properties of Solids (Academic Press, New York, 1972).Google Scholar