Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T03:25:17.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Coupled nonlinear Schrödinger equations for Langmuir and elecromagnetic waves and extension of their modulational instability domain

Published online by Cambridge University Press:  13 March 2009

M. R. Gupta ,
B. K. Som  and
Brahmananda Dasgupta
M. R. Gupta
Affiliation:
Centre of Advanced Study in Applied Mathematics, Calcutta University, Calcutta700 009, India
B. K. Som
Affiliation:
Department of Physics, B. K. Girls' College, Howrah, West BengalIndia
Brahmananda Dasgupta
Affiliation:
Saha Institute of Nuclear Physics, Calcutta700 009, India.
Get access Rights & Permissions [Opens in a new window]

Extract

A pair of coupled nonlinear Schrödinger equations for transverse and longitudinal waves has been derived. The coupling resulting from equalization of group velocities drives the Langmuir waves modulationally unstable for wavelengths shorter than (mi/me)½ λD and also extends the domain of modulational instability of electromagnetic waves when relativistic effects are taken into account. Instability is found to occur also for the perturbation wavenumber domain in which both the uncoupled Langmuir and electromagnetic waves are modulationally stable. This is shown to be caused by resonant four-wave interaction l + t → l′ + t′. 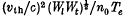The growth rate of the instability is, in general, of the order of but increases to the extent of a factor (c/vth)2 near the resonance 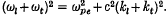Solitary wave solutions are given. Depending on the relative values of the self-modulation and coupling coefficients, the Langmuir or the transverse or both the waves may be localized in space.

Type
Articles
Information
Journal of Plasma Physics , Volume 25 , Issue 3 , June 1981 , pp. 499 - 507
Copyright
Copyright © Cambridge University Press 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berezhiani, V. I., Tsintsadze, N. L. & Tskhakaya, D. D. 1980 J. Plasma Phys. 24, 15.CrossRefGoogle Scholar
Das, K. P., & Sihi, S. 1977 Czech J. Phys. B 27, 1368.CrossRefGoogle Scholar
Inoue, Y. 1976 J. Plasma Phys. 16, 439.CrossRefGoogle Scholar
Kakutani, T., & Sugimoto, N. 1974 Phys. Fluids, 17, 1617.CrossRefGoogle Scholar
Kennel, C. F., & Pellat, R. 1976 J. Plasma Phys. 15, 335.CrossRefGoogle Scholar
Kaw, P. K., & Dawson, J. 1970 Phys. Fluids, 13, 472.CrossRefGoogle Scholar
Rudakov, L. I. 1973 Soviet Phys. Doklady, 17, 1166.Google Scholar
Sluijter, F. W., & Montgomery, D. 1965 Phys. Fluids, 8, 551.CrossRefGoogle Scholar
Shukla, P. K., Yu, M. Y. & Spatschek, K. H. 1977 Phys. Lett. 62 A, 332.CrossRefGoogle Scholar
Som, B. K., Gupta, M. R. & Dasgupta, B. 1979 Phys. Lett. 72 A, 111.CrossRefGoogle Scholar
Thornhill, S. G., & Ter Haar, D. 1978 Phys. Reports, 43, 44.CrossRefGoogle Scholar
Tsintsadze, N. L., Tskhakaya, D. D. & Stenflo, L. 1979 Phys. Lett. 72 A, 115.CrossRefGoogle Scholar
Washimi, H., & Taniuti, T. 1966 Phys. Rev. Lett. 17, 996.CrossRefGoogle Scholar